Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 7

Определение требуемого числа прогонов (экспериментов)

     Если указанными в п. 2. 2. 4 методами не определенно число экспериментов, то ведется специальный расчет. Для этого  используется два подхода:

1. Эмпирический подход используется, если искомая случайная величина не подчиняется нормальному закону распределения. На основе теории больших чисел проводится по каждой характеристике не менее 30 экспериментов.

2. Если случайная характеристика подчиняется нормальному закону распределения, то  используются специальные распределения (t-распределение и c²-распределение) для нахождения требуемого числа экспериментов, обеспечивающих заданную погрешность результатов.

     Допустим, определяем случайную характеристику æ с допустимой погрешностью e.

        Пусть æ- математическое ожидание искомой случайной характеристики. Из математической статистики известно, что оценка мат. ожидания e связана        с t-распределением (Стьюдента) следующим соотношением:

                                                ,

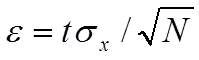       где t-случайная величина, подчиняющаяся t-распределению, задана таблично;

       s_x-среднеквадратичное отклонение, которое обычно задано или определяется из полученного статистического ряда по формуле: ;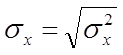

       N-число экспериментов.

Величина t определяется  из таблицы следующим образом: задаются число степеней свободы n=N-1 и уровень доверия q=1-p/2, где p-доверительная вероятность.

     Искомое число прогонов определяется по формуле:    .

Если в качестве æ выбирается дисперсия искомой случайной  характеристики, то требуемое число экспериментов вычисляется следующим образом. По известным из математической статистики формулам записывается выражение:

                                           ,

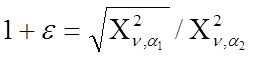где 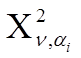-случайная величина, подчиняющаяся -распределению (Пирсона) и задана таблично. Для выбора из таблицы значения необходимо задать число степеней свободы n=N-1 и два уровня доверия a₁=1-p/2 и a₂=1-p/2. Далее по формуле находится такая степень свободы n, при которой

                                                   .

Требуемое число прогонов, при котором дисперсия будет определена с погрешностью меньше e, определяется по формуле N_пр=n+1.

Составление структуры моделирующего алгоритма

     Структура моделирующего алгоритма из ранее выбранных имитаторов составляется следующим образом:

1)Составляется структура алгоритма, реализующего основные функции модели.

В системах обслуживания это имитаторы входных потоков, имитаторы процесса обслуживания, имитаторы, определяющие правила обслуживания. Поскольку составляется имитационная модель, основой которой является воспроизведение процесса функционирования, то в первую очередь размещаются блоки, имитирующие входные потоки. Затем размещаются имитаторы процесса обслуживания (имитаторы обслуживающих аппаратов и очередей). Далее среди размещенных имитаторов устанавливают блоки или операторы, определяющие правила обслуживания.

2) В полученной структуре алгоритма размещают блоки по сбору и обработке данных, блоки по установке  начальных значений переменных, блоки, определяющие организацию проведения эксперимента (длительность эксперимента, число экспериментов и т. д.)

Описание полученного алгоритма

На этом этапе проводится описание блоков, входящих в состав алгоритма, с указанием их функционального предназначения и циркулирующих в них пере - менных. Например, если это массив, то его размерность и переменные. Затем  проводится подробное описание связей между блоками. Если в связях возникают конфликтные ситуации, то описываются способы выхода из них. Если необходимо уточнение какого-либо из блоков алгоритма, проводят его композицию (декомпо- зицию) с подробным описанием этой процедуры. Помимо этого проводится подробное описание входных и выходных данных, а также описываются способы оценки качества полученных результатов.

     Для того чтобы модель была законченным продуктом, алгоритм необходимо реализовать с помощью известных языков программирования или моделирования.

Пример построения моделирующего алгоритма,

основанного на принципе

Составим модель производственного процесса изготовления подшипника роликового типа. Задача исследования состоит в определении оптимальных интервалов времени между последовательными наладками оборудования. Для уменьшения внепроизводственных расходов типа простоя оборудования и затрат на содержание бригад наладчиков целесообразно увеличить длительность интервала времени между наладками, но при этом увеличивается доля бракованных подшипников.

Описание исследуемого процесса.

Подшипник включает в себя  n роликов. Качество подшипника определяется однородностью диаметров роликов – z(t). Желательно, чтобы все n роликов одного подшипника были по возможности одинакового диаметра.

Подшипник считается годным, если разброс диаметров, обозначенный U, не превышает заданной величины . Разброс диаметров не остаётся постоянным и зависит от продолжительности работы оборудования после очередной наладки.

Целью моделирования является получение зависимости доли брака от времени между наладками.  q = q(t).

Зависимость – случайная функция. Моделирующий алгоритм целесообразно строить по принципу , так как в системе отсутствуют особые состояния.

Построение моделирующего алгоритма.

1.  Выбор имитаторов основных функций.

Так как целью моделирования является определение доли брака q = q(t), зададим временной интервал от 0 до T_max. Следовательно, в алгоритме должен быть блок наращивания времени от 0 до T_max. Основной функцией изготовления подшипника является выпуск роликов диаметром z_k. Следовательно, необходим имитатор z_k , подчиняющаяся определённому закону.

Помимо формирователя z_k необходимы имитаторы проверки разброса диаметров роликов. Поэтому, необходимо предусмотреть в алгоритме следующие блоки:

- U = Z_max – Z_min , где Z_max – максимальный диаметр из выборки объёмом n;

                                  Z_min – минимальный диаметр из выборки объёмом n;

- Z_max =  {Z₁, Z₂,…, Z_n};

- Z_min = {Z₁, Z₂,…, Z_n}.