Моделирование систем управления. Формирование требований и разработка концептуальной модели. Разработка математической модели системы массового обслуживания, страница 13

2.  Если распределения совпадают, а адекватности не достигнуто, переходят к балансировке модели. На этом этапе модель изменяют таким образом, чтобы результаты совпадали.

3.  Если балансировка не приводит к адекватности модели, переходят к оптимизации. Оптимизация проводится следующим образом: из всех параметров выбирается наиболее значимый параметр (оказывающий на модель наибольшее влияние). Затем указанный параметр или же исключается из модели, или предлагается способ нивелирования (сглаживания) указанного параметра. Если оптимизация не приводит к адекватности, переходят к построению новой модели.

1. Сравнение распределений вероятности результатов

Адекватность может быть не достигнута в модели вследствие того, что законы распределения, принятые в модели, не соответствуют законам объекта (тем, которые действуют на объекте). Калибровка модели по этому пункту ведётся в следующей последовательности: в модель закладывают законы распределения, по предположению, близкие к объекту, или же изменяют модель таким образом, чтобы законы совпадали. Для того, чтобы проверить, насколько законы совпадают, используется критерий согласия  (критерий согласия Пирсона).

Для проверки по  степени совпадения (согласия) распределений проводятся следующие вычисления:

теоретическое определяется по таблице распределения при заданных значениях уровня доверия  и степенях свободы V = m-2, где m – число групп ряда распределения, составляющих статистическую совокупность (группа близких значений). Фактическое определяют по формуле: 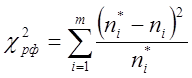, где   и  - частота попадания значений исследуемого параметра в соответствии с выбранным законом распределения и с теоретическим законом распределения ( на объекте).

Затем  сравнивается с . Если окажется, что , то выбранные законы распределения в модели совпадают с законами на объекте.

Далее при новых законах распределения проверяется адекватность модели. Если модель не адекватна, переходят ко 2-ому этапу – балансировке.

2. Балансировка модели

На этом этапе проводится изменение модели по каждому из параметров таким образом, чтобы результаты совпадали. Выполняется это следующим образом: в изменённой модели и на объекте изменяется параметр р в широком диапазоне. При этом при каждом значении параметра вычисляется сумма квадратов отклонения: 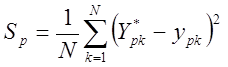  . Если найденная сумма квадратов S_р приняла минимальное допустимое значение, значит по параметру р достигнута балансировка. Далее проверяется адекватность сбалансированной модели. Если балансировка не даёт положительных результатов, переходят к оптимизации.

3. Оптимизация модели

На этом этапе определяется параметр, который наибольшим образом влияет на структуру и состав модели. Затем модель перестраивается таким образом, чтобы указанный параметр был незначительным или же исключён из модели. После каждого изменения модели проводится оценка значимости параметра, допустим, р_i. Для этого записывается линейная регрессия:  S_pi = a₀ + a₁p_i.

Затем проводится оценка значимости параметра а₁. Если в результате изменения модели коэффициент а₁ становится незначимым в регрессии, проводится проверка адекватности.

Если модель не адекватна, переходят к полной перестройке модели.

2. 7. Сети Петри

 При разработке структурных моделей дискретных систем в качестве базовой информации можно использовать данные о логической взаимосвязи наблюдаемых в системе событий и условий, определяющих наступление этих событий. Такого типа системы можно представить в виде последовательности наступления событий. Причем событие в системе наступает при выполнении определённых условий. Состоявшееся событие приводит к новым условиям. Вновь полученные условия достаточны для выполнения следующего события и т.д.

Если в системе циркулируют циклические процессы, то в итоге таких переходов (условия – события) система должна прийти в исходное состояние (значение) и далее вновь повторить рассмотренный цикл.

Представление такой последовательности позволяет описать структуру объекта с точки зрения процессов, протекающих в нём.

Модели таких систем поддерживаются математическим аппаратом сетей Петри. В сетях Петри условия, при которых в системе наступает событие, обозначается позициями и записывается в виде р_i, где i – число возможных условий в системе (i=1,2,…,Р); обозначается графически в виде окружности с указанием внутри имени позиции типа р_i.

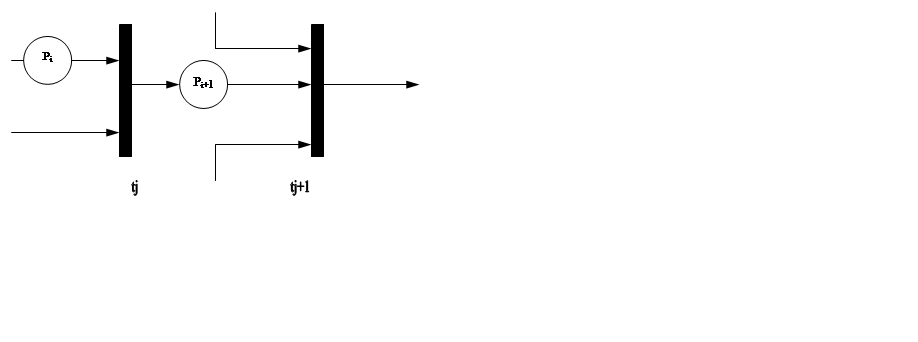
События, происходящие в системе, в сетях Петри обозначаются переходами t_j, где j – число возможных переходов в системе (j=1,2,…,Т); графически обозначается в виде планки, например, сеть Петри рис. 1.

Рис. 1

Для сети Петри определяется для каждого t_j-го перехода входные позиции (I(t_j)) и выходные позиции (O(t_j)). Для каждой позиции определяется входной переход – I (p_i) и выходной переход – O (p_i).

Для графической модели сети Петри: все позиции и переходы соединяются дугами. В результате сеть Петри представляет собой пространство С, определяющее Р, Т, Е:    С = (Р, Т, Е), где Р- множество позиций;

                                                               Т – множество переходов;

                                                               Е – множество дуг.

Е определяется как объединение всех входных и выходных дуг:

Е = (Р*Т) U (Т*Р).

Сети Петри могут быть представлены в виде графа (см. фрагмент рис. 1) или в виде матриц и вектора.

Матричная модель сети Петри

В матричной форме сеть Петри представляет собой пространство, состоящее из матриц R и вектора маркировок М_к. Для задания сети Петри необходимо определить матрицу R: матрицу R⁺ и матрицу R^- и начальный вектор маркировок М₀.:     С = (R⁺, R^-, M₀).

Матрица инцидентности R

Матрица инцидентности устанавливает взаимосвязь между позициями и переходами, строками которой являются переходы, столбцами – позиции.

Элементами матрицы являются r_ij, которые принимают следующие значения:

 

               1, если i-ая позиция является выходной для j-го перехода;                       

r_ij =      -1, если i-ая позиция является входной для j-го перехода;