Биоэлектричество и медицинская электроника: Учебное пособие, страница 7

Здесь - потенциал мембраны (общая шина – межклеточная жидкость), Е₁, Е₂, … Е_i – равновесные мембранные потенциалы различных типов ионов (K⁺, Na⁺, Cl^– и т.д.), R₁, R₂, … R_i – сопротивления ветвей (каналов), I₁, I₂, … I_i – токи ветвей (каналов).

Потенциал  в данном случае находится из условия . Ток каждой ветви определяется формулой 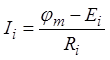. Подставив полученное в предыдущую формулу, приведем ее к виду 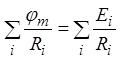, из которого с учетом 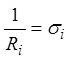 и следует соотношение (8). Эквивалентная схема особенно убедительно свидетельствует о необходимости учета ветвей с  () при расчете мембранного потенциала.

Мембранный потенциал имеет большое значение в жизнедеятельности организма. Существование его является одним из факторов, обеспечивающих процессы метаболизма: за счет мембранного потенциала осуществляется электрический транспорт различных веществ в клетку и из нее. Мембранный потенциал обеспечивает также защиту клетки от воздействия внешних электрических полей. Суть этой защиты сводится к тому, что значение напряженности поля в мембране, обусловленное ее собственным потенциалом, во много раз превосходит напряженности электрических полей стандартной среды обитания на Земле. В самом деле, порядок напряженности поля внутри мембраны (а именно напряженность является силовой функцией электрического поля, ) определяется как отношение мембранного потенциала  к толщине мембраны d: .

Для характерных = 100 mB и d = 10 нм напряженность поля составляет 10 кВ/мм. Это громадная величина. Она является предельной для вакуумных приборов, т.е. только в вакууме могут быль реализованы столь большие поля. В обычной же среде обитания человека (при атмосферном давлении 760 мм рт.ст., температуре ~ 20 °С) удельные напряженности не превышают 1 кВ/мм, т.е. имеют примерно на порядок меньшие значения, чем в мембране. Это связано с тем обстоятельством, что в большинстве случаев область, в которой создается электрическое поле (переменное или постоянное) превышает длину свободного пробега в газе при давлении 760 мм рт.ст. и температуре 20 °С. Поэтому увеличение поля сверх 1 кВ/мм приводит к пробою газа и шунтированию источника напряжения, формирующего поле. И только в том случае, если протяженность пространства, в котором существует поле, не превышает длины свободного пробега в газе, т.е. воздух при давлении 760 мм рт.ст. удовлетворяет определению понятия вакуума, пробой может не наступить. Длина свободного пробега в воздухе в стандартных условиях имеет порядок l=10^-7–10^-8 м =10-100 нм. Чтобы протяженность области поля с напряженностью до 10 кВ/мм не превышала l, необходимо, чтобы это поле было переменным и имело длину волны l порядка l, т.е. l » 10-100 нм. Такую длину волны имеют рентгеновские лучи и примыкающие к ним электромагнитные волны в области вакуумного ультрафиолета. Излучение с этими и меньшими длинами волн могут оказать существенное влияние на процессы на мембране клетки и в ее объеме.

Таким образом, мембранный потенциал имеет чрезвычайно важное значение для существования организма.

1.3. Возбуждение мембраны. Потенциал действия

Нервные и мышечные клетки обладают особенностью, которая отличает их от клеток других органов и тканей. Особенность эта заключается в том, что потенциал их мембраны перестает линейно зависеть от воздействия при превышении последним определенного уровня. Параметры импульса напряжения на мембране (амплитуда и длительность) при этом определяются лишь характеристиками мембраны и окружающих ее электролитов. Процесс изменения напряжения на мембране клетки, характеризующийся нелинейными и параметрическими проявлениями в ответ на внешнее воздействие, называется возбуждением. Максимальное напряжение на мембране, возникающее при ее возбуждении внешним сигналом, превышающим пороговый уровень, называется потенциалом действия (ПД). Механизм возбуждения нервных и мышечных клеток лежит в основе информационной системы организма. Полагают, что упомянутые клетки в процессе эволюции сменили некоторые функции, связанные с транспортом веществ через мембрану, на функции, обеспечивающие информационный обмен между различными структурами. Качественно картина изменения потенциала мембраны нервной клетки при различных уровнях воздействия  представлена на рис. 6 (потенциал отсчитывается от внешней поверхности мембраны, точнее, от точки в объеме межклеточной жидкости, близкой к поверхности мембраны).

В покое мембрана имеет потенциал , определяемый формулой (8) (в данном случае мы заменили разность потенциалов  с неопределенной точкой отсчета потенциалом, отсчитываемым от внешней поверхности мембраны). При анализе переходных процессов под воздействием внешнего источника электрического тока в эквивалентной схеме мембраны должнабыть учтена ее емкость С. Заменив суммарное действие всех источников  с проводимостями  (рис. 5) одним источником  с проводимостью 1/R, эквивалентную схему для качественного рассмотрения изменений мембранного потенциала при внешнем воздействии можно представить в виде, изображенном на рис. 7.

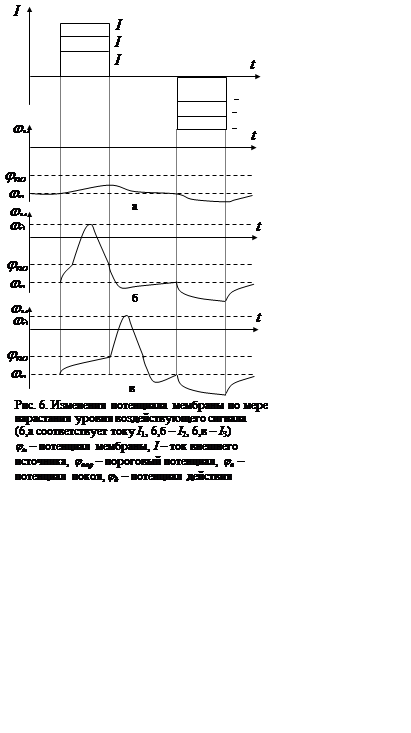При подключении мембраны к цепи внешнего источника питания I(t) потенциал ее j начинает изменяться по закону, определяемому дифференциальным уравнением 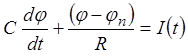. Учитывая, что в момент подключения источника тока потенциал мембраны был равен потенциалу покоя , и полагая, что I(t) представляет собой импульсный ток прямоугольной формы амплитудой  и длительностью , решение уравнения можно представить следующим образом:

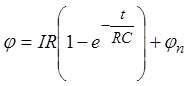.                           (16)