1.2. Потенциал покоя
Отличие концентраций носителей зарядов в цитоплазме и межклеточной жидкости и селективная проницаемость мембраны обусловливают возникновение разности потенциалов между содержимым клетки и окружающей ее средой. Механизм возникновения этой разности качественно может быть объяснен следующим образом.
Допустим, имеются два электрически нейтральных раствора с различными концентрациями ионов одноименных атомов и мембрана, проницаемая лишь для определенных носителей заряда. Для простоты положим вначале, что она проницаема для ионов одного типа атомов. Если жидкости привести в соприкосновение с мембраной (одну с одной, а другую с другой сторонами), то под действием градиента концентрации ионы, для которых мембрана проницаема, будут переходить из среды с большей концентрацией в среду с меньшей. При этом из первой среды во вторую будет переноситься заряд, что приведет к нарушению электронейтральности каждой из сред и возникновению между ними электрического поля, возрастающего по мере увеличения количества зарядов, пересекших мембрану.
Сила, действующая на ион, порожденная этим полем, имеет направление, противоположное направлению силы концентрационного градиента. Через некоторое время эти силы уравнивают друг друга, и поток ионов через мембрану теряет преимущественное направление, ионный ток через каналы мембраны становится равным нулю. Система приходит к стационарному состоянию, характеризуемому определенной разностью потенциалов между содержимым клетки и окружающей ее средой. В зависимости от особенностей сред эта разность потенциалов может быть сосредоточена в основном либо в растворах, примыкающих к мембране, либо в ней самой. В случае, когда мембрана проницаема для нескольких типов ионов, равновесный потенциал, устанавливаемый на ней, определяется равенством нулю суммарного тока, переносимого всеми ионами. Этот потенциал может не совпадать с равновесным потенциалом какого-либо из ионов.
Если бы мембраны не существовало, то при соприкосновении растворов возникла бы диффузионная разность потенциалов. Однако она уменьшалась бы по мере взаимного проникновения растворов и полностью исчезла через некоторое время.
Получим соотношения для
количественной оценки мембранного потенциала. Как было отмечено, равновесный
потенциал определяется из условия равенства нулю суммарного тока через мембрану
ионов различных атомов. Рассмотрим случай произвольного числа ионов, способных
пересечь мембрану. Плотность диффузионного тока ![]() для
i-го компонента в предположении об изменении
концентрации только в направлении, перпендикулярном к мембране, пропорциональна
градиенту концентрации
для
i-го компонента в предположении об изменении
концентрации только в направлении, перпендикулярном к мембране, пропорциональна
градиенту концентрации ![]() , взятому с отрицательным
знаком, коэффициенту диффузии
, взятому с отрицательным
знаком, коэффициенту диффузии ![]() и величине заряда
иона
и величине заряда
иона ![]() :
:
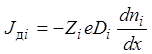 .
.
Символ «e»
обозначает абсолютное значение заряда электрона, ![]() -
знак заряда иона и степень его ионизации.
-
знак заряда иона и степень его ионизации.
Плотность тока
проводимости ![]() пропорциональна напряженности
электрического поля Е, обусловленного суммарным зарядом всех ионов, прошедших
через мембрану, подвижности данного иона
пропорциональна напряженности
электрического поля Е, обусловленного суммарным зарядом всех ионов, прошедших
через мембрану, подвижности данного иона ![]() ,
его концентрации
,
его концентрации ![]() и величине заряда иона:
и величине заряда иона:
![]()
(величина ![]() взята
по модулю, т.к. направления поля и тока должны совпадать).
взята
по модулю, т.к. направления поля и тока должны совпадать).
Плотность тока ![]() , обусловленная ионами определенного
типа, будет равна
, обусловленная ионами определенного
типа, будет равна
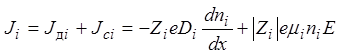 .
.
Плотность тока J, обусловленная всеми ионами, для которых проницаемость мембраны отлична от нуля, находится как сумма токов отдельных видов ионов
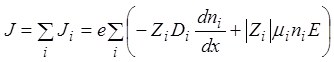 . (1)
. (1)
В стационарном состоянии полный ток в любом сечении, параллельном плоскости мембраны, равен нулю. Используя это обстоятельство, из (1) можно получить формулу для напряженности электрического поля:
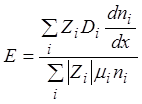 . (2)
. (2)
Необходимо отметить, что полученное соотношение справедливо для любой точки как в окружающих мембрану растворах, так и в самой мембране.
Электрическое поле
должно удовлетворять также уравнению Пуассона ![]() .
С учетом
.
С учетом ![]() в случае зависимости параметров лишь
от одной координаты оно запишется в виде:
в случае зависимости параметров лишь
от одной координаты оно запишется в виде:
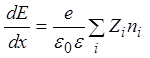 , (3)
, (3)
где ![]() -
концентрация i-того типа иона в данной среде
(растворе или мембране).
-
концентрация i-того типа иона в данной среде
(растворе или мембране).
Положив ![]() , (2) и (3) можно свести к системе
уравнений:
, (2) и (3) можно свести к системе
уравнений:
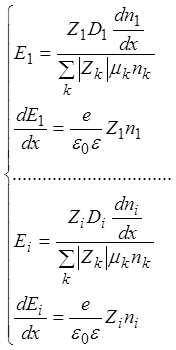 . (4)
. (4)
Число уравнений в системе равно
удвоенному количеству типов ионов, способных проникать через мембрану. При этом
не имеет значения, отличаются или нет концентрации ионов данного типа в объемах
электролитов по разные стороны мембраны. Решение системы (4) представляет
значительные сложности, во-первых, из-за большого количества уравнений
вследствие прозрачности мембраны для многих ионов, во-вторых, из-за
необходимости ее решения отдельно для каждой из областей (цитоплазмы, мембраны,
межклеточной жидкости) и последующего «сшивания» на границах и, в-третьих,
вследствие того, что входящие в уравнение параметры ![]() и
и
![]() сами могут быть функциями координат,
определяемыми характером поля и распределением концентраций ионов. Эти
обстоятельства заставляют искать приближенные решения. Преобразуем для этого
формулу (2). Произведение
сами могут быть функциями координат,
определяемыми характером поля и распределением концентраций ионов. Эти
обстоятельства заставляют искать приближенные решения. Преобразуем для этого
формулу (2). Произведение ![]() представляет
собой удельную проводимость
представляет
собой удельную проводимость ![]() в той или иной
точке для ионов i-того типа. Выражение
в той или иной
точке для ионов i-того типа. Выражение ![]() представим в виде
представим в виде
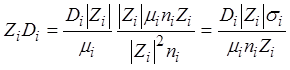 .
.
Коэффициент
диффузии ![]() и подвижность
и подвижность ![]() связаны между собой соотношением
Эйнштейна
связаны между собой соотношением
Эйнштейна 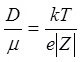 , где T – абсолютная температура,
k – постоянная Больцмана. Тогда
, где T – абсолютная температура,
k – постоянная Больцмана. Тогда 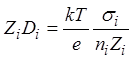 . Подставив это в (2) и используя
. Подставив это в (2) и используя ![]() , получим выражение для дифференциала
напряжения:
, получим выражение для дифференциала
напряжения:
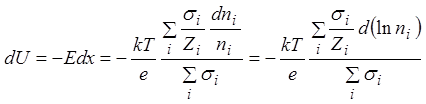 . (5)
. (5)
Уравнение (5) позволяет находить разность потенциалов между различными точками в растворах или мембране.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.