Биоэлектричество и медицинская электроника: Учебное пособие, страница 20

Длина межперехватного расстояния в миелинизированных волокнах обеспечивает надежную передачу сигнала при прекращении функционирования, по крайней мере, одного перехвата, т.е. на расстоянии двух пассивных участков потенциал возбуждения перехвата Ранвье остается выше порогового. Скорость распространения сигнала в этих волокнах в основном определяется скоростью в пассивных участках и временем возбуждения перехвата. Скорость в пассивных участках находится из полученной ранее формулы для пассивных волокон. Однако в случае миелинизированных волокон необходимо учитывать толщину изоляции, вследствие чего входящие в формулу для скорости параметры С и G необходимо уточнить. Емкость должна определяться формулой для цилиндрического конденсатора: 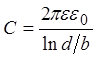, где С – емкость на единицу длины, d – внешний диаметр волокна, b – диаметр внутренней части (перехвата Ранвье), e₀ = 0,885×10^-11 Ф/м – электрическая постоянная, e - относительная диэлектрическая проницаемость миелина. Сопротивление единицы длины мембраны  можно определить, проинтегрировав выражение для сопротивления единицы длины слоя толщиной dx и радиусом x:

,

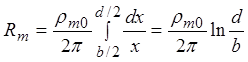где  - объемное удельное сопротивление, определяемое традиционным способом и измеряемое в Ом×м.

Выражение для скорости в этом случае приобретает вид:

 .

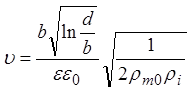Обозначив b/d = t, получим уравнение 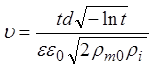, из которого следует, что зависимость скорости от отношения b/d носит немонотонный характер: при крайних значениях t = 0 и t = 1 u = 0. Следовательно, существует оптимальное значение b/d, при котором скорость достигает максимального значения. Оно определяется из условия . Проведя соответствующие выкладки, получим . Реальные значения b/d примерно соответствуют оптимальному.

Оценим скорость проведения сигнала в пассивной части миелинизированного волокна. В качестве исходных выберем параметры из рассмотренного ранее примера для пассивного волокна, полагая d=0,2 мм, =1 Ом×м, значением b зададимся из условия оптимальности: b » 0,607d. Удельное сопротивление мембраны оценим величиной , где D - толщина мембраны. Сопротивление  положим таким же, как и в рассмотренном выше примере (= 1 Ом×м²), а D = 10 нм = 10^-8 м. Диэлектрическую проницаемость мембраны примем равной двум. Подстановка этих значений в формулу для скорости дает u » 300 м/с. С учетом времени на возбуждение перехвата Ранвье значение скорости несколько уменьшится. Таким образом, скорость распространения сигнала в миелинизированных волокнах в десятки раз превышает скорости проведения в однородных пассивных и активных волокнах.

Полученный вывод справедлив, однако, лишь для волокон, диаметр которых превышает определенное минимальное значение. В самом деле, из формулы для скорости в миелинизированном волокне следует, что при заданном значении t зависимость от диаметра волокна носит линейный характер. В то же время, как уже упоминалось, в соответствии с (32) скорость в активном волокне определяется квадратным корнем из диаметра. При малых аргументах функции вида  с показателем, меньшим единицы, превосходят функции qz с показателем a = 1 (p, q, a - параметры, z – независимая переменная) . Однако при z ® ¥ характер отношения функций меняется на противоположный. Следовательно, существует точка пересечения этих функций, в которой обе зависимости дают одинаковый результат. Определим эту точку, например, для волокна с параметрами рассмотренных выше аксона кальмара и пассивного участка миелинизированного волокна. Приравняем скорости для обоих случаев, считая диаметр волокна d независимой переменной

.

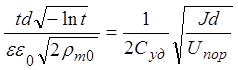В правой части ток на единицу длины I₀₁ – I₀₂ заменен на плотность ток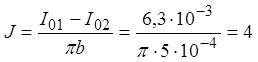а А/м², С на 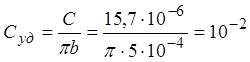Ф/м². Удельную проводимость аксомплазмы в обоих волокнах полагаем одинаковой. Подставив численные значения, получаем  мкм. Таким образом, в данном случае миелинизированные волокна толще 0,25 мкм имеют преимущество в скорости распространения сигнала в сравнении с немиелинизированными.

2.2.2. Прохождение сигнала через неоднородности

Кроме периодической неоднородности, характерной для миелинизированных аксонов, волокна могут иметь еще и непериодические нарушения структуры поперечного сечения: плавно или ступенчато изменять диаметр, ветвиться, контактировать с такими же или другими биологическими тканями посредством специальных окончаний, именуемых синапсами. Кроме этого, нервные волокна, обычно собранные в пучок (нервный ствол), могут взаимодействовать между собой в пространственных областях той или иной протяженности. В пассивных волокнах задача о распространении сигнала в неоднородных или (и) взаимодействующих участках наиболее полно решается методами электродинамики. Упрощенные решения могут быть получены путем использования теории «длинных линий». Решения эти характеризуются терминами «падающая волна», «отраженная волна», «прошедшая волна», «коэффициент отражения», «коэффициент прохождения» и другими.

В возбудимых волокнах характер распространения сигналов в областях нерегулярности существенно отличается как по механизму, так и по терминам, описывающим его.

Рассмотрим качественно процессы, происходящие в области неоднородности для двух случаев.

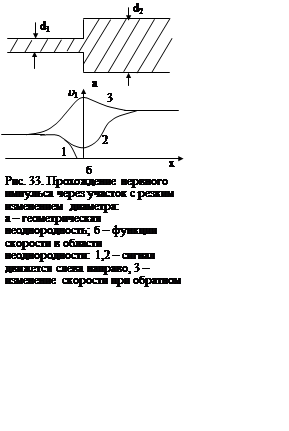Первый – скачок диаметра (рис. 33). Положим вначале, что сигнал движется из области с малым диаметром в область с большим. В соответствии с моделью мембранного генератора при движении по однородному участку волокна вдали от неоднородности появлению тока возбуждения предшествует отрезок с эффективной длиной 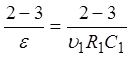 ( - параметры тонкой части волокна), в котором потенциал изменяется от  практически до нуля. По мере приближения к неоднородности все большая часть этого отрезка оказывается в широкой области. При этом средняя емкость на единицу длины эквивалентной длинной линии увеличивается, что приводит при постоянстве заряда в подпороговом отрезке к уменьшению потенциала в сравнении с . Последнее обусловливает уменьшение скорости в узкой области по мере приближения к неоднородности. После перехода неоднородности вступает в действие мембранный генератор широкой области волокна, ток на единицу длины которой больше, чем в области с малым диаметром (при одинаковых плотностях тока). Это приводит к увеличению заряда, переносимого через мембрану, увеличению напряжения на ней и скорости. На некотором расстоянии от неоднородности последняя приобретает стационарное значение, превышающее стационарное значение для узкой области (кривая 2).