Биоэлектричество и медицинская электроника: Учебное пособие, страница 5

Удельные проводимости окружающих мембрану электролитов могут зависеть от координат. Однако в случае малых возмущений концентраций ионов этим обстоятельством можно пренебречь. В мембране же степень изменения концентрации может быть достаточно большой: отношение концентраций того или иного иона на границах мембраны приблизительно равно их отношению в объемах цитоплазмы и межклеточной жидкости и варьирует в диапазоне от единиц до сотен раз (см. табл. 1, 2, 3). Однако и в этом случае удельную проводимость для конкретного типа ионов можно приближенно считать постоянной. Ионное облако внутри мембраны (отвлекаясь от ее дискретной структуры и считая мембрану гомогенной средой) можно рассматривать как идеальный газ одноименно заряженных частиц. Удельная проводимость идеального газа определяется произведением подвижности на концентрацию заряженных частиц . Подвижность заряженной частицы в идеальном газе пропорциональна длине свободного пробега . Последняя, в свою очередь, обратно пропорциональна концентрации всех частиц среды . Таким образом, . В случае газа, состоящего лишь из заряженных частиц, концентрация переносчиков тока  совпадает в каждой точке с концентрацией всех частиц среды (). Вследствие этого можно приближенно считать удельную проводимость каналов каждого типа ионов постоянной. Отличия же проводимостей мембраны для различных ионов обусловлены особенностями внутреннего строения соответствующих каналов и их количеством.

Учитывая изложенные обстоятельства, проинтегрируем (5) в пределах толщины мембраны и найдем падение напряжения на ней  (пределы интегрирования по U от  - потенциала одной стороны мембраны, до  - потенциала другой стороны, при этом концентрации изменяются от  на одной стороне до  - на другой)

.

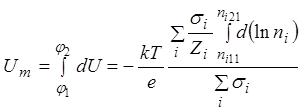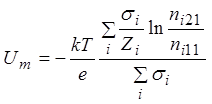.                                     (6)

Если мембрана проницаема лишь для одного типа ионов, то

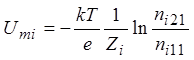.                                        (7)

Сравнивая (6) и (7), можно заключить, что разность потенциалов на мембране в общем случае определяется как среднее взвешенное разностей потенциалов отдельных типов ионов

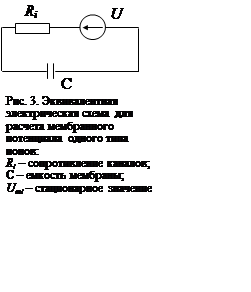
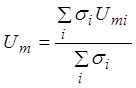.              (8)

Из последней формулы следует, что если мембрана проницаема лишь для одного типа ионов из совокупности имеющих концентрационный градиент, то падение напряжения на ней не будет зависеть от проводимости. Такой вывод подтверждается и эквивалентной схемой (рис. 3), из которой видно, что напряжение на конденсаторе (мембране) в установившемся режиме будет равно  при любых значениях . Резистор  определяет лишь время заряда конденсатора , но не максимальное напряжение на нем. Перенося этот вывод на реальную мембрану, можно заключить, что разность потенциалов на мембране, создаваемая конкретным типом ионов, не зависит от внутренней структуры ее каналов.

Относительное постоянство удельных проводимостей сред позволило упростить решение системы (4), сведя его к вычислению равновесных потенциалов отдельных типов ионов и нахождению их среднего взвешенного значения. Однако в формулу (7) входят значения концентраций на границах мембраны, которые сложно определить в эксперименте. Вследствие этого возникает необходимость установления связи между граничными концентрациями и концентрациями в объемах окружающих растворов, в которых проведение измерений более просто. Для решения задачи запишем уравнения для потенциала какого-либо одного (i-того) типа ионов:

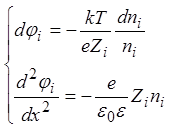.                              (9)

Интегрируя первое уравнение системы, можно установить связь между потенциалами и концентрациями в различных точках

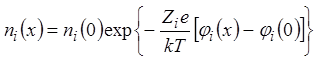,                 (10)

где n(x) и j(x) – концентрация и потенциал в исследуемой точке, n(0) и j(0) – то же самое в точке, принятой за начало отсчета.

Все рассматриваемые среды, взятые изолированно, электронейтральны. Лишь при их контакте нарушается однородность и возможны разделение зарядов и возникновение электрического поля.

Концентрация  определяется поэтому из условия электронейтральности среды в объеме (вдали от границы). Каждую компоненту i можно считать одной из составляющих симметричного бинарного электролита, т.е. полагать, что каждому типу ионов определенного знака соответствует другой тип ионов противоположного знака с той же самой концентрацией. Однако через мембрану способен проникать лишь один тип. Из-за этого у границы нарушается электронейтральность среды и возникает электрическое поле. Таким образом, , т.е.  является разницей концентраций положительных () и отрицательных () зарядов.

Формула (10) позволяет записать выражение для концентраций зарядов следующим образом:

.

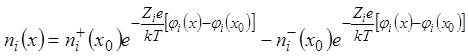Учитывая, что в объеме , соотношение можно упростить:

.

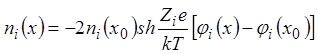Комбинируя это со вторым уравнением системы (9), приходим к дифференциальным уравнениям для потенциала в различных средах:

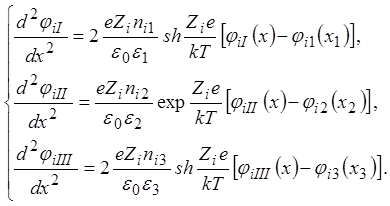        (11)

Первое и третье уравнения относятся к цитоплазме и межклеточной жидкости, второе – к мембране. Эту систему необходимо дополнить граничными условиями. Первое из них – равенство потенциалов, второе – равенство индукций  на границе раздела первых двух сред и   - на границе раздела второй и третьей сред. 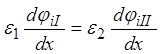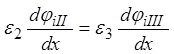Последние условия могут быть выражены также через производные потенциалов:  - на границе первой и второй сред и  - на границе второй и третьей сред.

Система дает возможность в принципе найти непрерывную функцию потенциала для всех сред. Однако аналитическое решение ее без каких-либо упрощающих предположений весьма сложно. Получим приближенное решение, разложив правые части уравнений в ряд Тейлора и удерживая в нем лишь члены порядка не выше первого (отбросим также для простоты индекс i):

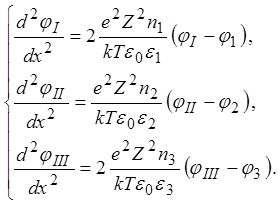
Решения упрощенной системы запишутся следующим образом:

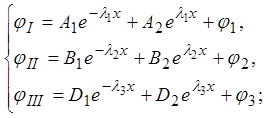                          (12)

; ; .

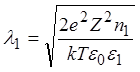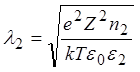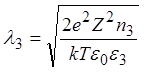Параметр 1/l характеризует расстояние, на котором изменение потенциала (т.е. разделение зарядов) еще существенно. Он называется Дебаевской длиной экранирования.

Для получения конкретных соотношений введем систему координат. Начало ее совместим с границей первой и второй сред. Таким образом, первая среда будет полностью располагаться в области отрицательных значений независимой переменной, а вторая и третья займут область положительных значений. Тогда из условия конечности  при x ® -¥ необходимо A₁ = 0. Отсчитывая потенциал из объема первой среды  и опуская индекс при A₂, находим: