Физика \ Биофизика

Биоэлектричество и медицинская электроника: Учебное пособие, страница 15

В пп. 2, 3 и 4 время, необходимое для заряда хронирующего конденсатора С2 , эквивалентно рефракторному периоду биологической мембраны: если конденсатор С2 не заряжен до стационарного уровня, то выходной импульс либо отсутствует вообще, либо имеет меньшие длительность и амплитуду при любой величине входного напряжения.

2. РАСПРОСТРАНЕНИЕ МЕМБРАННОГО ПОТЕНЦИАЛА

Рассмотренное выше относится к случаю, когда размеры клеточной мембраны и скорость распространения сигнала по ней таковы, что можно пренебречь запаздыванием потенциала, т.е. считать, что при возмущении мембраны во всех ее точках одновременно устанавливается одинаковый потенциал. Это позволяет упростить анализ, ограничившись лишь колебательными явлениями. Реально же это допущение, особенно в случае нервных клеток, не выполняется, и возникает необходимость исследования процессов распространения возмущения.

Механизм распространения сигнала в нервных волокнах может носить пассивный и активный характеры. В первом случае, имеющем место в невозбудимых нервных клетках, а также в возбудимых при уровне возбуждения ниже порогового, сигнал распространяется, как в обычных волноведущих устройствах, эквивалентные схемы которых содержат лишь пассивные индуктивности, емкости и резисторы. Как правило, в реальных линиях такого рода декремент затухания имеет положительное значение, т.е. амплитуда сигнала уменьшается по мере удаления от места возмущения.

Во втором случае, имеющем место в возбудимых волокнах, амплитуда сигнала не изменяется по мере его распространения. Постоянство амплитуды обусловлено тем, что в данном случае распространение сигнала сводится к перемещению по волокну области с возбужденным состоянием.

Рассмотрим каждую из этих ситуаций в отдельности.

2.1. Распространение сигналов в пассивных волокнах

Аксон нервной клетки в первом приближении можно рассматривать как отрезок цилиндрического волновода, заполненного проводящей средой с определенной диэлектрической проницаемостью, имеющего проводящую стенку и погруженного во внешнюю среду, также характеризующуюся собственной проводимостью и диэлектрической проницаемостью. Решение задачи для пассивной мембраны (или активной мембраны в подпороговом режиме) в этом случае не представляет принципиальных математических трудностей, однако оказывается весьма громоздким.

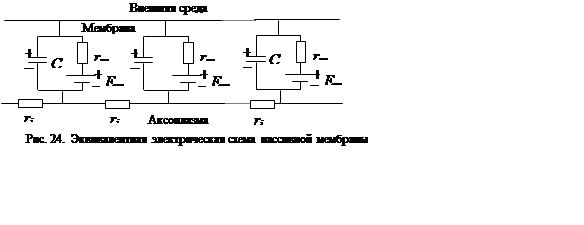
На практике считают, что в нервном волокне существует лишь поперечное электромагнитное поле, и моделируют аксон направляющей системой в виде коаксиальной линии. Эквивалентная электрическая схема этой линии (рис. 24) предполагает эквипотенциальность внешней среды из-за ее гораздо большей проводимости в сравнении с проводимостью внутреннего объема (при необходимости проводимость внешней среды может быть учтена путем корректировки проводимости аксоплазмы ).  - источник ЭДС, величина которой определяется, в основном, градиентом концентрации ионов калия на мембране. Конденсатор С отражает емкость мембраны, а резистор  - ее проводимость.


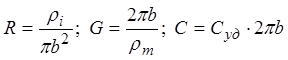Для переменного тока расчетная схема упрощается и представляется в виде длинной линии, состоящей лишь из пассивных элементов (рис. 25). В этой схеме R – сопротивление аксоплазмы на единицу длины волокна, С и G - соответственно емкость и проводимость мембраны на единицу длины. Величины R, С и G  связаны с удельными параметрами соотношениями:


,

где  - удельное сопротивление аксоплазмы, Ом×м;  - удельное сопротивление мембраны, Ом×м2;  - удельная емкость мембраны, Ф/м2; b – радиус аксона.

Как видно из эквивалентной схемы, аксон в сравнении с технической проводной линией (содержащей в идеальном случае лишь LC- элементы) является чрезвычайно плохой канализирующей системой, т.к. содержит элементы R и G, обусловливающие диссипацию  энергии в процессе распространения.

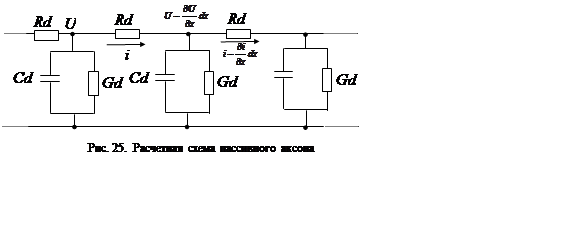
Используя обозначения, приведенные на рис. 25, составим «телеграфные» уравнения для рассматриваемой линии (положим, что расстояние между узлами в схеме равно dx). Задача решается для полубесконечной линии:

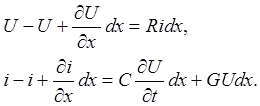
Продифферецировав первое уравнение по x и комбинируя со вторым, получаем:

.

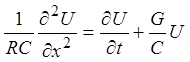Это уравнение в частных производных параболического типа. Введя обозначения , , приведем его к виду:

.

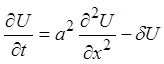Сделав замену переменных , приходим к параболическому уравнению для функции V в канонической форме:

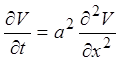.                                      (21)

Рассмотрим реакцию системы на возмущающее воздействие. Сигнал произвольной формы может быть разложен в ряд Фурье, т.е. представлен в виде суммы синусоидальных составляющих. Поэтому достаточно исследовать реакцию системы на синусоидальный сигнал и проанализировать частотную зависимость отклика. В соответствии со сказанным зададим граничные условия для функции U(x, t) в виде: , т.е. исследуем отклик системы на косинусоидальное или синусоидальное воздействие в ее начале (x=0). Используя , упрощаем запись граничного условия: . В этом случае действительная часть решения соответствует косинусоидальному воздействию на границе, а мнимая – синусоидальному.

Для функции  граничное условие запишется как

.               (22)

Решение (21) с граничным условием (22) будем искать в виде:

,                             (23)

где a - неопределенный пока коэффициент.

Подставив (23) в (21), находим его значение:

.

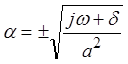Чтобы решение было затухающим по мере увеличения x (x > 0), нужно выбрать перед корнем отрицательный знак. Итак, .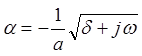

Записав комплексное число под корнем в показательной форме 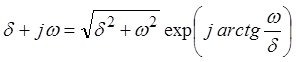 и осуществив операцию извлечения корня, приходим к выражению: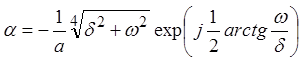 и, далее, 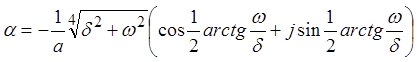. После преобразований окончательно получаем:

.

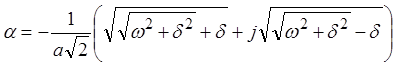Используя полученное выражение, а также (23) и связь функций V(x, t) и U(x, t), потенциал исследуемой канализирующей системы можно представить в виде:

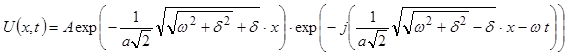. (24)

Исследуем полученное выражение.

1. Сигнал распространяется по аксону с затуханием, постоянная которого 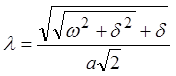 увеличивается с ростом частоты, т.е. чем выше частота возмущающего сигнала, тем на меньшее расстояние он распространяется. Подставив вместо а и d их значения и выразив l через параметры линии 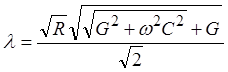, можно видеть, что эффект увеличения постоянной затухания с частотой обусловлен шунтирующим действием емкости мембраны. Минимальное значение l соответствует w ® 0 и равно . Оценим l, выразив R и G через удельные параметры мембраны:

Скачать файл