При определенных условиях возбуждение из области с малым диаметром может вообще не проникнуть в область с большим диаметром, т.е. в ней не разовьется механизм генерации потенциала действия (кривая 1). Расчеты, основанные на модели генератора тока, приводят для этого случая к следующему неравенству:
,
где d1 и d2 – диаметры узкой и широкой областей
волокна, K – отношение максимального значения
напряжения на мембране в пике возбуждения (потенциал действия) к пороговому
напряжению 
.
При движении сигнала из широкой
части в узкую пороговое явление отсутствует – сигнал проходит при любом
соотношении диаметров, удовлетворяющих условию 
.
При подходе к границе участков его амплитуда увеличивается вследствие
уменьшения средней емкости в подпороговой части импульса при сохранении амплитуды
тока на единицу длины волокна, равной значению для широкой части. По мере
перехода через неоднородность величина тока уменьшается и скорость спадает до
значения, характерного для узкой ветви (кривая 3).
Интересно отметить качественно
противоположный характер порогового условия перехода через неоднородность в
случае передачи электромагнитной энергии по замкнутым волноведущим структурам и
рассмотренным биологическим переносчикам электрического сигнала. В случае
волноводов сигнал всегда передается (конечно, частично отразившись) из области
с меньшим диаметром в область с большим. Из области же с большим диаметром в
область с меньшим сигнал передается только в том случае, если его частота
превышает величину, определяемую из соотношения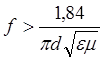 
,
где d – диаметр узкой области волновода, e и m
- соответственно диэлектрическая и магнитная проницаемости его внутренней
части.
В качестве второго примера рассмотрим неоднородность типа «ветвление». В общем случае ветвление характеризуется тем, что сигналы, распространяющиеся по определенному количеству волокон (M), в узле переходят в другое количество (N). В зависимости от соотношения M и N, диаметров волокон, моментов подхода сигналов из набора М к узлу возможны различные ситуации. Простейшими являются случаи, когда сигнал из одной ветви переходит в две другие, и наоборот, из двух ветвей в одну (рис. 34). В первом случае (рис. 34, а) в зависимости от соотношения диаметров волокон могут реализовываться следующие сценарии.
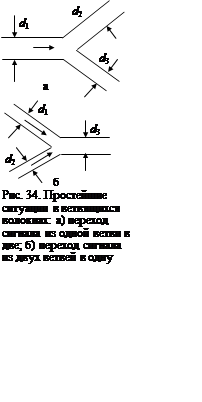1. Если площадь на единицу длины
волокна, по которому сигнал подходит к узлу ветвления, превышает суммарную площадь
единицы длины отходящих волокон, то сигнал всегда проходит в них и имеет место
эффект увеличения скорости в ветви «d1» при
подходе к узлу.
2. Если соответствующая площадь меньше, то сигнал в ветви «d1» затормаживается по мере подхода к узлу вплоть до полной остановки при выполнении условия
.
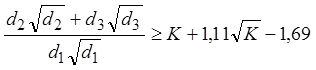Во втором случае (рис. 34, б) также могут иметь место различные ситуации.
1. Суммарная площадь единицы длины волокна d1 и d2 меньше соответствующей площади волокна d3 , и выполняется условие:
.
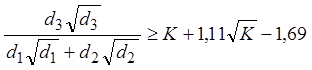В этом случае сигналы из ветвей диаметрами d1 и d2 вместе или порознь не вызывают возбуждения ветви с диаметром d3.
2. Тот же, что и в п.1, случай, но условие пункта не выполняется. Причем не выполняется оно лишь для суммарной площади ветвей d1 и d2, но выполняется для каждой из ветвей в отдельности по отношению в ветви d3. Тогда сигналы, распространяющиеся по волокнам d1 и d2, могут проникнуть в волокно d3 лишь при условии их одновременного прихода к узлу ветвления. В противном случае каждый из сигналов остановится в области узла.
3. Условие блокирования не выполняется для одной из ветвей d1 или d2 по отношению к двум другим. В данной ситуации сигнал из ветви, для которой условие блокирования не выполняется, всегда проходит в две другие. Сигнал же из волокна, для которого условие блокирования выполняется, может пройти лишь при поддержке сигнала из другого волокна.
4. Условие блокирования не выполняется для обеих ветвей. В этом случае сигналы из ветвей d1 или d2 всегда проникают в d3.
Таким образом, даже простейший узел ветвления может выполнять несколько формально логических функций. В частности, пп. 2 и 4 второго случая являются примером реализации логических функций «И» и «ИЛИ» на биологической элементной базе.
Работа любого органа или ткани организма сопровождается процессами, природа которых носит электрический характер. Перенос ионов через мембраны клеток создает в межклеточной жидкости токи, приводящие из-за конечной проводимости среды к возникновению между различными точками разности потенциалов. При достаточной интенсивности процессов электрические сигналы могут быть зафиксированы и на внешних границах соответствующих структур, и даже на кожной поверхности организма в целом. Электрические поля, создаваемые функционирующими органами, в той или иной степени отражают их (органов) состояние и могут иметь большое значение в качестве диагностического признака. Область медицины, изучающая функционирование органов и тканей на основе анализа создаваемых ими электрических полей, называется электрографией. Прямая и обратная задачи электрографии формулируются следующим образом.
Прямая – исследование механизмов электрической активности и разработка методов регистрации и анализа биопотенциалов с внешних поверхностей организма или составляющих его структур.
Обратная – диагностика состояния органов и тканей по пространственно-временному распределению генерируемых ими электрических сигналов.
Термин «электрограмма», как правило, конкретизируется названием органа или ткани, электрическая активность которых исследуется. В настоящее время в той или иной степени разработаны «электроэнцефалография» – электрограмма мозга, регистрируемая на поверхности головы, «электромиография» – запись сигналов электрической активности мышечной ткани, осуществляемая с кожных покровов исследуемых мышц, «электроретинография» – фиксация электрических потенциалов сетчатки глаза с помощью электродов, размещаемых на роговице глаза и кожной поверхности рядом с ней, «электрогастрография» – электрограмма гладкой мышцы желудка, снимаемая с определенной части поверхности тела, «электрокардиография» – регистрация потенциалов, создаваемых мышцей сердца.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.