Биоэлектричество и медицинская электроника: Учебное пособие, страница 6

.

При таком выборе отсчета потенциала n₁ представляет собой концентрацию заряженных частиц, способных проникать через мембрану, в объеме первой среды. Потенциал  при x = 0 равен . В этом случае в соответствии с (10) концентрация зарядов на границе первой и второй сред равна n₂. Третья среда располагается в области x ³ d (d – толщина мембраны). Вначале осуществим «сшивание» при x = 0:

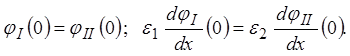
Выполнение соответствующих процедур приводит к уравнениям для определения коэффициентов:

.

Использование 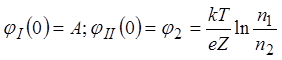 позволяет определить функцию потенциала в мембране:

.

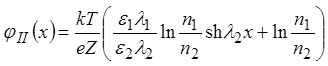Потенциал в третьей среде с учетом , а также принимая во внимание, что начало отсчета в этом случае сдвинуто вправо относительно начала координат на толщину мембраны, можно представить следующим образом:

,

где  - потенциал в объеме третьей среды: .

Соответственно концентрация в объеме третьей среды равна n₃ и связана с концентрацией в объеме первой среды соотношением, вытекающим из (10): 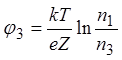. При x=d также должны выполняться условия равенства потенциалов и индукций

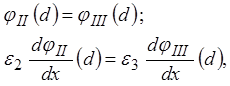
из которых следует:

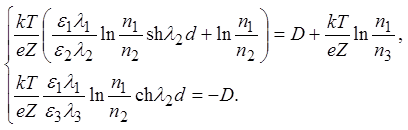
Неизвестными в данной системе являются потенциал на границе первой и второй сред 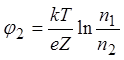 и разность между потенциалами в объеме третьей среды и на границе третьей среды с мембраной –D. Каждое уравнение является нелинейным, т.к. параметр l₂ также зависит от n₂. Упростим уравнения, полагая , вследствие чего n₁ » n₂ и 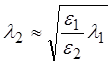. Тогда вычислительные процедуры приводят к

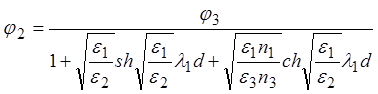,                   (13)

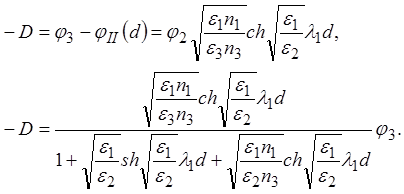                (14)

Учитывая, что диэлектрические проницаемости окружающих мембрану растворов (e₁ ~ e₃ ~ 80) значительно превосходят диэлектрическую проницаемость мембраны (e₂ ~ 2-3), при достаточно больших d и отношениях концентраций n₁/n₃ знаменатель (13) значительно превосходит единицу. Следовательно, и падением напряжения в первой среде можно пренебречь.

При выполнении условия 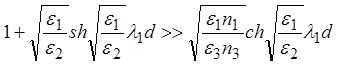 можно пренебречь и падением напряжения в третьей среде и считать приближенно падение напряжения на мембране равным .

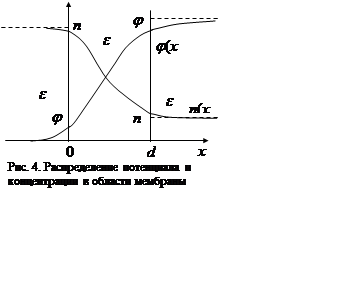Качественно зависимости j(x) и n(x) представлены на рис. 4.

Для большинства ионов, окружающих мембрану, условия малости падения напряжения в электролитах выполняются. Поэтому в формуле (7) значения концентраций на границах мембраны  и  можно заменить на значения концентраций в объемах электролитов  и

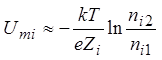.     (15)

В тех же случаях, когда условия не выполняются (например, для Са⁺⁺ в клетке мышцы сердца), необходимо определять приближенное значение концентраций на границах из (13) и (14).

Получим теперь в качестве примера значения мембранных потенциалов для некоторых ионов. В процессе формирования мембранного потенциала основная роль принадлежит ионам калия, натрия, хлора и кальция. Найдем равновесный мембранный потенциал, к примеру гигантского аксона кальмара, создаваемый тем или иным ионом в отсутствие остальных. Используем данные табл. 1 и положим, что измерения проводятся при температуре Т=300 К. При этом kT/e » 26 mB.

Равновесный потенциал ионов калия (Z_i=1):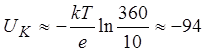 mB.

Равновесный потенциал ионов натрия (Z_i=1): 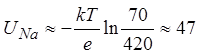mB.

Равновесный потенциал ионов хлора (Z_i=-1): 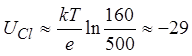mB.

Равновесный потенциал ионов кальция (Z_i=2): 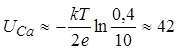mB.

Совокупный потенциал мембраны аксона кальмара , обусловленный действием ионов рассмотренных атомов, определяется в соответствии с (8) как среднее взвешенное равновесных потенциалов отдельных ионов:

,

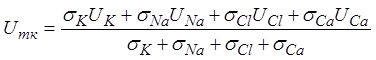где  - проводимости соответственно ионов калия, натрия, хлора и кальция.

В состоянии покоя проводимости для различных ионов составляют пропорцию  (проводимость кальция в аксоне кальмара в состоянии покоя чрезвычайно мала). Тогда

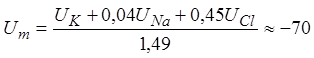 mB.

Оценим количество ионов, переносимых через мембрану, для обеспечения равновесного потенциала. Для простоты будем считать клетку шаром диаметром D. Емкость мембраны С при этом равна произведению удельной емкости  на площадь обкладки, которая в данном случае будет определяться площадью поверхности шара: . Заряд на обкладке конденсатора , деленный на число Фарадея F=96500 Кл/моль, определяет количество ионов вещества  (в молях), транспортированных через мембрану,

.

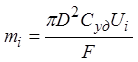Относительное изменение количества ионов данного вещества в цитоплазме в результате трансмембранного переноса  определится как отношение перенесенного количества ионов  ко всему их количеству в объеме клетки , равного :

.

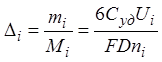Оценим  на примере ионов калия.

= 1 мкФ/см² = 10^-2 Ф/м²; = 94 mB » 10^-1 В;  F ~ 10⁵ Кл/моль;

D ~ 15 мкм = 1,5×10^-5 м; » 400 ммоль/л = 4×10² моль/м³.

Подстановка численных значений дает =10^-5, т.е. относительное изменение составляет 10^-3 %.

Таким образом, для создания равновесного потенциала на мембране клетки требуется относительно небольшое количество ионов, и это количество тем меньше, чем меньше размеры клетки, равновесный потенциал данного иона и больше его концентрация в объеме клетки.

Необходимо отметить, что результаты расчета мембранного потенциала, учитывающие только ионы, имеющие градиенты концентраций при переходе через мембрану, могут оказаться неверными, если в обеих средах присутствуют дополнительно ионы с нулевой разницей концентраций в объемах по обе стороны мембраны, но способные проникать через нее. Согласно (8) даже при равенстве нулю одного из напряжений , но , отличном от нуля, влияние данного типа ионов на полный потенциал мембраны может быть существенным, особенно при большой проводимости ионов с одинаковой концентрацией в объемах цитоплазмы и межклеточной жидкости, в сравнении с проводимостями других, проникающих через мембрану. Физически это означает шунтирование током данного типа ионов мембранного потенциала. Эквивалентным элементом электрической модели каналов таких ионов будет резистор.

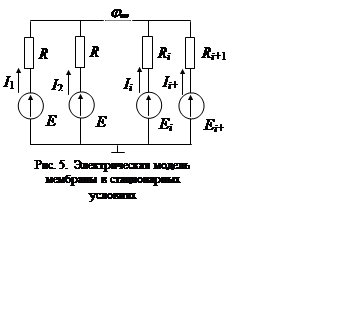Формула (8) позволяет построить и общую электрическую модель мембраны. Если рассматривать напряжения , создаваемые отдельными типами ионов на мембране, как источники электродвижущей силы , а  - как проводимости резисторов , то уравнение (8) с точки зрения теории электрических цепей представляет собой не что иное, как выражение для потенциала в методе узловых потенциалов для электрической схемы, изображенной на рис. 5.