1. Процессы переноса ионов натрия и калия независимы друг от друга и осуществляются по пространственно разделенным каналам двух видов, каждый из которых специфичен только для определенного типа ионов.
2. Нелинейные проявления мембранного тока обусловлены изменением проницаемостей каналов во времени под действием электрического поля в мембране.
 Для количественного объяснения
результатов экспериментальных исследований английские ученые А.Ходжкин и
А.Хаксли предложили математическую модель процессов в мембране клетки. Первоначально
речь шла о задаче возбуждения гигантского аксона кальмара, однако оказалось,
что метод применим и в общем случае. Суть его сводится к представлению мембраны
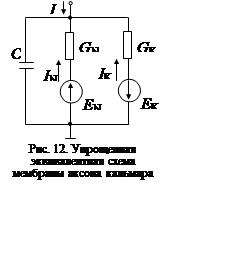
в виде электрической схемы из соединенных параллельно емкости и резисторов,
причем последовательно с частью резисторов включены источники ЭДС, отражающие
равновесные потенциалы ионов, участвующих в транспорте через мембрану. В случае
аксона кальмара простейшей является модель, содержащая лишь две активные ветви:
натриевую, отражающую ток ионов и равновесный потенциал натрия, и калиевую,
моделирующую процессы переноса калия (рис. 12).
Для количественного объяснения
результатов экспериментальных исследований английские ученые А.Ходжкин и
А.Хаксли предложили математическую модель процессов в мембране клетки. Первоначально
речь шла о задаче возбуждения гигантского аксона кальмара, однако оказалось,
что метод применим и в общем случае. Суть его сводится к представлению мембраны
в виде электрической схемы из соединенных параллельно емкости и резисторов,
причем последовательно с частью резисторов включены источники ЭДС, отражающие
равновесные потенциалы ионов, участвующих в транспорте через мембрану. В случае
аксона кальмара простейшей является модель, содержащая лишь две активные ветви:
натриевую, отражающую ток ионов и равновесный потенциал натрия, и калиевую,
моделирующую процессы переноса калия (рис. 12).
Изменение заряда
мембраны во времени ![]() определяется суммой токов,
протекающих через нее:
определяется суммой токов,
протекающих через нее:
![]() ,
,
где ![]() -
натриевый и калиевый токи, I – ток внешнего
источника. Учитывая связь между падением напряжения на мембране V и током отдельной ветви, уравнение для
-
натриевый и калиевый токи, I – ток внешнего
источника. Учитывая связь между падением напряжения на мембране V и током отдельной ветви, уравнение для ![]() можно записать в виде:
можно записать в виде:
![]() .
.
Заряд мембраны обусловливает на ее емкости напряжение V = Q/C, что при постоянстве емкости проводит к соотношению:
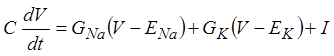 . (17)
. (17)
Это уравнение определяет все
многообразие поведения мембраны клетки при различных внешних воздействиях и
начальных условиях. Сложность его решения связана с тем, что проводимости ![]() и
и ![]() (а
в общем случае это могут быть и проводимости каналов других ионов) зависят от
мембранного потенциала и времени:
(а
в общем случае это могут быть и проводимости каналов других ионов) зависят от
мембранного потенциала и времени: ![]() ;
; ![]() . В настоящее время еще не развита
теория, связывающая макроскопические параметры и характеристики транспортных
систем мембраны (в частности, проводимости) с процессами в ней на молекулярном
уровне. Вследствие этого решение (17) для конкретного случая требует проведения
достаточно сложных (из-за малости размеров клеток) экспериментальных
исследований, по результатам которых получают функции проводимостей в той или
иной форме.
. В настоящее время еще не развита
теория, связывающая макроскопические параметры и характеристики транспортных
систем мембраны (в частности, проводимости) с процессами в ней на молекулярном
уровне. Вследствие этого решение (17) для конкретного случая требует проведения
достаточно сложных (из-за малости размеров клеток) экспериментальных
исследований, по результатам которых получают функции проводимостей в той или
иной форме.
Ходжкин и Хаксли предложили аппроксимирующие выражения для проводимостей в виде двух функций, одна из которых зависит лишь от напряжения V, а другая – от обеих переменных. Калиевая проводимость определяется соотношением
![]() ,
,
 где
где ![]() -
максимальное значение калиевой проводимости, а n подчиняется
дифференциальному уравнению
-
максимальное значение калиевой проводимости, а n подчиняется
дифференциальному уравнению ![]() , решение
которого
, решение
которого ![]() характеризует долю открытых каналов
и изменяется от нуля до единицы (
характеризует долю открытых каналов
и изменяется от нуля до единицы (![]() и
и ![]() - значения n
при t = 0 и в установившемся режиме
соответственно,
- значения n
при t = 0 и в установившемся режиме
соответственно, ![]() ). Функции
). Функции ![]() и
и ![]() определяют
зависимость скоростей процессов открывания и закрывания каналов от напряжения
на мембране.
определяют
зависимость скоростей процессов открывания и закрывания каналов от напряжения
на мембране.
С ростом
напряжения относительно уровня потенциала покоя ![]() увеличивается,
а
увеличивается,
а ![]() уменьшается по экспоненциальному
закону (рис.13). Монотонно возрастает также установившееся значение n (рис.14).
уменьшается по экспоненциальному
закону (рис.13). Монотонно возрастает также установившееся значение n (рис.14).
Зависимость натриевой проводимости
от времени носит экстремальный характер: возрастающая ветвь обусловлена
процессами активации каналов, а спадающая – инактивации. Вследствие этого она
описывается двумя функциями (m и
h), каждая из которых определяется из
соответствующего дифференциального уравнения 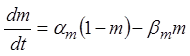 или
или
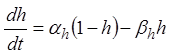 . Как и в случае калиевой
проводимости, m(V, t) и h(V, t) определяют
соотношения процессов активации и инактивации, а коэффициенты
. Как и в случае калиевой
проводимости, m(V, t) и h(V, t) определяют
соотношения процессов активации и инактивации, а коэффициенты ![]() устанавливают ход этих процессов в
зависимости от напряжения. Использование введенных функций позволяет представить
натриевую проводимость в виде:
устанавливают ход этих процессов в
зависимости от напряжения. Использование введенных функций позволяет представить
натриевую проводимость в виде:
![]() ,
,
где ![]() -
максимальное значение.
-
максимальное значение.
Экспериментально установлено, что показатели степени 3 (для m) и 1 (для h) наиболее полно отражают ход натриевой проводимости.
Решения
кинетических уравнений для m и h аналогичны полученному выше: ![]() ,
,
![]() ,
, 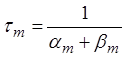 ,
,
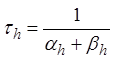 . Значения
. Значения ![]() и
и
![]() определяются из условий dm/dt = 0, dh/dt = 0 и выражаются
соотношениями:
определяются из условий dm/dt = 0, dh/dt = 0 и выражаются
соотношениями: ![]() ,
, ![]() .
.
Графическая
интерпретация зависимостей ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() представлена на рис. 15, 16.
представлена на рис. 15, 16.
В аналитической форме ![]() выглядят следующим образом:
выглядят следующим образом:
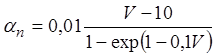 ,
, 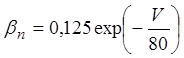 ,
,
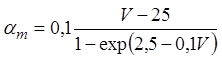 ,
, 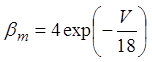 ,
,
![]() ,
, 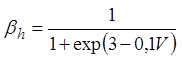 .
.
 С
помощью рассмотренной совокупности уравнений Ходжкин и Хаксли с большой
точностью подтвердили многочисленные экспериментальные результаты и сделали
предсказания относительно некоторых экспериментально не изученных особенностей
поведения мембраны аксона кальмара. Модель Ходжкина-Хаксли после некоторых изменений
оказалось возможным применить для исследования процессов электрического
возбуждения структур нервных клеток и других организмов.
С
помощью рассмотренной совокупности уравнений Ходжкин и Хаксли с большой
точностью подтвердили многочисленные экспериментальные результаты и сделали
предсказания относительно некоторых экспериментально не изученных особенностей
поведения мембраны аксона кальмара. Модель Ходжкина-Хаксли после некоторых изменений
оказалось возможным применить для исследования процессов электрического
возбуждения структур нервных клеток и других организмов.

Многочисленные экспериментальные исследования, а также результаты расчетов, основанных на уравнениях Ходжкина-Хаксли, позволили сформулировать некоторые общие свойства, характеризующие возбуждение нервных и мышечных клеток.
Порог возбуждения. Возникновение и развитие регенеративного процесса на мембране (потенциал действия) требует приложения внешнего возбуждения, превышающего определенный пороговый уровень. Под пороговым понимается потенциал, устанавливающийся на мембране в результате воздействия внешнего тока, после достижения которого с необходимостью возникает регенеративный процесс возбуждения. При этом амплитуды токов коротких и длинных импульсов, как правило, неодинаковы. Различие пороговых смещений потенциала для малых и больших длительностей может быть объяснено следующим образом. За время действия короткого возмущающего импульса натриевая проводимость существенно не изменяется, т.е. механизм регенерации за это время еще не развивается, хотя потенциал мембраны к моменту окончания импульса может значительно повыситься. После окончания импульса тока потенциал спадает, однако еще превышает потенциал покоя. Вследствие этого натриевая проводимость и, следовательно, натриевый ток начинают увеличиваться. Если натриевый ток достигнет уровня, при которомУважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.