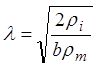Биоэлектричество и медицинская электроника: Учебное пособие, страница 16

.

Зададимся численными значениями: = 10⁴ Ом×см² = 1 Ом×м²;

 = 10² Ом×см = 1 Ом×м; b = 0,2 мм = 2×10^-4 м. Подставив их в последнюю формулу, приходим к значению l = 1 1/см. Величина 1/l характеризует расстояние, на котором сигнал ослабляется в «е» раз. Хотя 1/l и мало в сравнении с размерами позвоночных, для мелких существ, например насекомых, этого расстояния вполне достаточно для передачи сигнала без дополнительных затрат энергии.

Качественно характер зависимости l от параметров линии передачи (R, G) можно объяснить тем, что каждый элементарный отрезок линии представляет собой делитель из соединенных последовательно резисторов R и 1/G. Напряжение, снимаемое с G, тем больше, чем меньше R и G и, следовательно, тем больше расстояние, на которое распространяется заданный уровень.

Оценим частоту сигнала, на которой постоянная затухания увеличивается в два раза в сравнении с постоянной затухания при w = 0

.

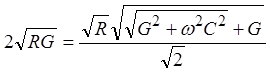После преобразований частота , соответствующая двукратному увеличению l, определяется соотношением , что приводит после выражения G и С через удельные параметры к .  Принимая  = 1 мкФ/см² = 10^-2 Ф/м, = 1 Ом×м², получаем  Гц.

2. Определим скорость распространения сигнала по нервному волокну.

Фазовая скорость  определяется как скорость поверхности постоянной фазы, т.е. ;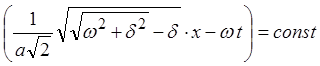

.

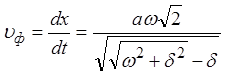Отсюда следует, что нервное волокно характеризуется сильной дисперсией: . Таким образом, сложный сигнал, представляемый суммой гармонических составляющих, будет искажаться по мере распространения. В области низких частот, определяемых в данном случае неравенством w << d с учетом 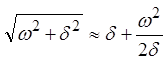, фазовая скорость перестает зависеть от частоты

.

Подстановка значений a и d  дает .

Отсутствие дисперсии означает, что в области низких частот групповая скорость , т.е. скорость переноса энергии, также равна .

В общем случае групповая скорость может быть определена из соотношения

.

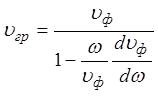Записав 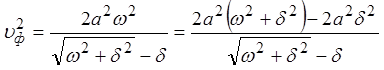, используя  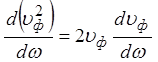и 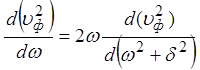, можно прийти к выражению:

.

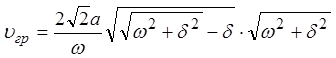В области низких частот 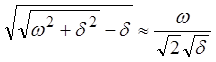  групповая скорость перестает зависеть от частоты и совпадает (как и должно быть) с фазовой.

При w ® ¥, ® ¥, что означает несправедливость формулы в области высоких частот. В этом случае скорость должна определяться из решения задачи в электродинамической постановке.

Оценим величину скорости распространения сигнала в пассивном волокне. Для конкретного примера выберем значения b, ,  такими же, как и в случае вычисления l, а значение удельной емкости  примем равным 1 мкФ/см². Формула для скорости, выраженная через удельные параметры волокна, примет вид:

.

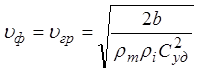После подстановки численных значений получаем м/с. Для биологических объектов, имеющих размеры около сантиметра, этой скорости вполне достаточно: время распространения сигнала имеет порядок единиц миллисекунд, что обеспечивает требуемую быстроту реакции. На малых расстояниях несущественна также дисперсия: разница в фазовых скоростях гармоник сигнала в этом случае еще не приводит к сильному искажению волнового пакета.

Качественно характер зависимости скорости от параметров линии может быть объяснен тем, что постоянная времени цепи заряда и разряда конденсатора С определяется параллельными R и 1/G, т.е. отношением R/G. Чем меньше это отношение и емкость конденсатора С, тем быстрее осуществляются его заряд и разряд, а следовательно, увеличивается скорость передачи возмущения.

Из формулы для скорости видно, что она может быть увеличена, при прочих равных условиях, путем увеличения диаметра волокна. Однако этот путь приводит к тому, что нервные волокна (а их для анализа жизненной ситуации и реакции на нее необходимо достаточно много) начинают занимать значительное место в организме. Поэтому большой диаметр имеют, как правило, только волокна, наиболее важные для жизнедеятельности.

2.2. Распространение сигнала в возбудимых волокнах

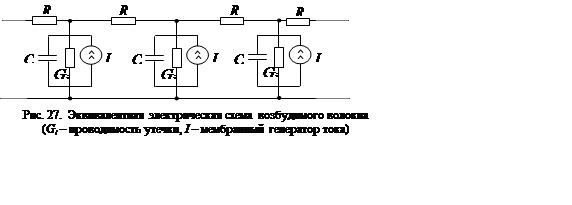
Механизм распространения сигнала в возбудимых нервных волокнах при уровнях, превышающих пороговый, существенно отличается от механизма передачи сигнала по линиям с проводниками, выполненными из металла. Если в последних ток практически одинаков во всех сечениях (при длине линии меньшей четверти длины волны), то в первых он неодинаков и отличен от нуля лишь в локальной области, перемещающейся по волокну. Распространение сигнала в этом случае иллюстрируется рис. 26. На нем изображено распределение зарядов и потенциала мембраны аксона для нескольких моментов времени.

Из рисунка видно, что сигнал по нервному волокну распространяется в виде локализованного в пространстве возмущенного участка. Токи через мембрану текут только в пределах этого участка. Слева к области возбуждения примыкает область в состоянии рефрактерности (через нее импульс возбуждения уже прошел), а справа – невозмущенная область. Вследствие этого сигнал распространяется только слева направо, захватывая невозмущенные участки по мере увеличения потенциала на фронте возмущенных до порогового уровня. Особенностью распространяющегося сигнала является постоянство его ампли-туды, определяемой потенциалом действия данного типа нервного волокна (например, в случае аксона кальмара натриевым потенциалом).

Количественный анализ процесса распространения импульса возбуждения по нервному волокну наиболее полно может быть осуществлен на основании уравнений Ходжкина-Хаксли. Однако эта система не допускает относительно простых аналитических решений. Вследствие этого используют различные упрощающие приемы. В частности, полученное ранее уравнение для пассивного волокна может быть распространено и на возбудимое, если учесть зависимость проводимости мембраны G от времени и потенциала. На практике, однако, заменяют произведение GU на эквивалентный генератор тока. С учетом проводимости утечки  расчетная эквивалентная электрическая схема аксона приобретает вид, показанный на рис. 27.

Уравнение для потенциала мембраны U рассматриваемой канализирующей системы может быть записано следующим образом:

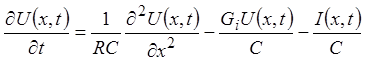.                    (25)