Учитывая, что каждая точка
мембраны волокна после прохождения возбужденного участка приобретает исходный
потенциал, можно считать, что суммарный заряд, протекший через нее 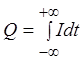 , должен быть равен нулю. Из этого
следует, что ток, протекающий через мембрану при ее возбуждении, должен быть
двуполярным. После достижения потенциалом мембраны на фронте возбуждения
порогового значения ток начинает втекать внутрь аксона (этот процесс обеспечивается
ионами натрия), а после достижения потенциалом действия вытекать из него за
счет активации калиевых каналов.
, должен быть равен нулю. Из этого
следует, что ток, протекающий через мембрану при ее возбуждении, должен быть
двуполярным. После достижения потенциалом мембраны на фронте возбуждения
порогового значения ток начинает втекать внутрь аксона (этот процесс обеспечивается
ионами натрия), а после достижения потенциалом действия вытекать из него за
счет активации калиевых каналов.
 Наиболее просто моделировать
мембранный генератор двуполярным прямоугольным импульсом тока (рис. 28). Он
включается, как только потенциал мембраны достигает порогового уровня.
Наиболее просто моделировать
мембранный генератор двуполярным прямоугольным импульсом тока (рис. 28). Он
включается, как только потенциал мембраны достигает порогового уровня.
Сравнение результатов решения (25) с генератором двуполярных прямоугольных импульсов тока, экспериментальных данных и строгого решения уравнений Ходжкина-Хаксли показывает, что, например, в случае аксона кальмара диаметром 0,5 мм наилучшее совпадение получается, если I1 = 63 мкА/см, I2 = 40 мкА/см, t1 – t0= 0,35 мс, t2 - t1 =0,55 мс (I1 и I2 – токи на единицу длины волокна).
Упрощая решение (25), обычно переходят из лабораторной в движущуюся со скоростью перемещения возмущенного участка систему координат. Для этого вводят новую переменную (обозначим ее Q), связанную с x и t соотношением Q = x - u t, где u - искомая скорость распространения импульса возмущения.
Тогда 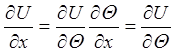 ;
;
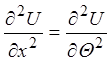 ;
; 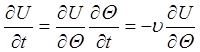 и
(25) приобретает вид:
и
(25) приобретает вид:
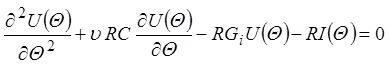 .
(26)
.
(26)
 Таким образом, путем перехода в
движущуюся систему координат удалось свести дифференциальное уравнение в
частных производных к обыкновенному дифференциальному уравнению. Введенная выше
функция I(t)
определяла возбуждение короткого участка мембраны, в котором запаздыванием распространения
сигнала можно было пренебречь и считать потенциал одинаковым на всей
поверхности мембраны. При переходе к движущейся системе координат для сохранения
соотношения между током и возбужденным участком переменную t
в I необходимо заменить на Q. При решении (26) за начало координат (Q = 0) принимается точка, в которой начинается
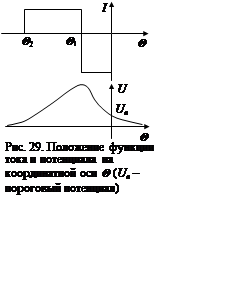
возбуждение мембраны. Взаимное положение функции тока и потенциала возбужденного
участка мембраны показано на рис. 29.
Таким образом, путем перехода в
движущуюся систему координат удалось свести дифференциальное уравнение в
частных производных к обыкновенному дифференциальному уравнению. Введенная выше
функция I(t)
определяла возбуждение короткого участка мембраны, в котором запаздыванием распространения
сигнала можно было пренебречь и считать потенциал одинаковым на всей
поверхности мембраны. При переходе к движущейся системе координат для сохранения
соотношения между током и возбужденным участком переменную t
в I необходимо заменить на Q. При решении (26) за начало координат (Q = 0) принимается точка, в которой начинается
возбуждение мембраны. Взаимное положение функции тока и потенциала возбужденного
участка мембраны показано на рис. 29.
Для упрощения анализа решим (26) в
предположении нулевой утечки (![]() = 0). Из-за
разрывного характера функции тока I(Q) решение приходится искать в четырех областях:
= 0). Из-за
разрывного характера функции тока I(Q) решение приходится искать в четырех областях:
1) 0 < Q < ¥;
2) Q1 < Q £ 0;
3) Q2 < Q £ Q1;
4) -¥ < Q £ Q2.
Таким образом, получается четыре выражения функции потенциала. Для того чтобы она была непрерывной вместе со своей первой производной во всей области изменения независимой переменной, результаты, полученные для частных областей, «сшиваются» на границах путем приравнивания функций и производных. Решение при этом оказывается хотя и не сложным, но весьма громоздким.
|
![]() (Q
£ 0, a
>0, b>0).
(Q
£ 0, a
>0, b>0).
 Изменяя
соотношения между I01, I11, I02,
I12, a и b (рис.
30), можно получать то и ли иное соотношение между амплитудами положительного и
отрицательного импульсов тока, а также изменять длительность входящего тока.
Изменяя
соотношения между I01, I11, I02,
I12, a и b (рис.
30), можно получать то и ли иное соотношение между амплитудами положительного и
отрицательного импульсов тока, а также изменять длительность входящего тока.
В правой полуплоскости I(Q)=0 и (26) окажется однородным
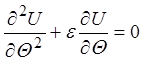 ,
,
где обозначено: e
= uRC.
Решение этого уравнения ![]() содержит две
произвольные постоянные А1 и А2. Требование
ограниченности UI при Q®¥ приводит к А2=0. Значение
А1 будет определено из условий «сшивания» решений для
положительной и отрицательной полуосей.
содержит две
произвольные постоянные А1 и А2. Требование
ограниченности UI при Q®¥ приводит к А2=0. Значение
А1 будет определено из условий «сшивания» решений для
положительной и отрицательной полуосей.
В области Q < 0 уравнение для потенциала неоднородно:
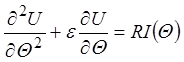 . (27)
. (27)
Его решение можно
записать в виде суммы, состоящей из общего решения однородного и частного
решения неоднородного уравнения: ![]() .
.
Решение
однородного уравнения определяется зависимостью ![]() .
Из условия конечности U02 при Q ®
- ¥ и, учитывая e = uRC >0, получаем А3
= 0. Значение А4 определим из требования равенства функций UI и UII,
а также их первых производных при Q
= 0. Частное решение неоднородного уравнения будем искать в виде суммы членов,
составляющих выражение для тока
.
Из условия конечности U02 при Q ®
- ¥ и, учитывая e = uRC >0, получаем А3
= 0. Значение А4 определим из требования равенства функций UI и UII,
а также их первых производных при Q
= 0. Частное решение неоднородного уравнения будем искать в виде суммы членов,
составляющих выражение для тока
![]() ,
,
где g, h, c, d - неизвестные коэффициенты.
Подставив U12 в (27) и приравняв коэффициенты при однородных членах, найдем значение упомянутых коэффициентов:
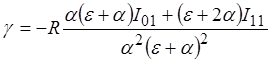 ,
, 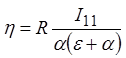 ,
,
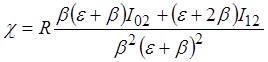 ,
, 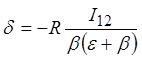 .
(28)
.
(28)
Определим теперь
постоянные А1 и А4 из условий равенства
функций UI и UII
и их первых производных при Q =
0. Первое условие дает ![]() . Условие
равенства производных приводит к соотношению
. Условие
равенства производных приводит к соотношению ![]() ,
из которого, используя (28), можно сразу найти А1:
,
из которого, используя (28), можно сразу найти А1:
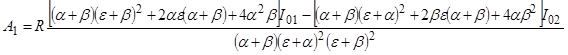 . (29)
. (29)
Комбинируя следствия из первого и второго условий, приходим к выражению, определяющему А4:
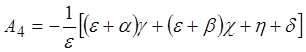 .
.
Подставив вместо g, h, c, d их значения из (28), после некоторых упрощений получаем формулу, связывающую А4 с параметрами тока, элементов эквивалентной схемы и скоростью
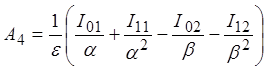 . (30)
. (30)
Учтем теперь то обстоятельство, что после окончания возбуждения (по истечении рефрактерного периода) каждый участок нервного волокна возвращается в исходное состояние, т.е. на нем устанавливается потенциал, существовавший до начала возбуждения. Это возможно в том случае, если количество заряда, втекающего внутрь волокна, равно количеству заряда, вытекшего из него, т.е. суммарный заряд Q, протекший через мембрану в любом сечении за бесконечный интервал времени, должен быть равен нулю:
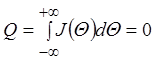 ,
, 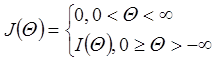 .
.
Подстановка значения J(Q) приводит к выражению
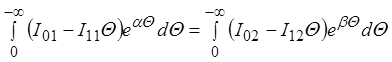 ,
,
из которого следует:
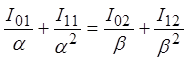 .
.
Сравнивая
последнее соотношение с (30), можно видеть, что условие Q = 0
приводит к А4 = 0. Это же условие обеспечивает одинаковость
значений А1, полученных из равенства функций при Q = 0 (А1=g+c)
и равенства производных в этой же точке 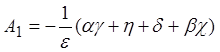 .
В самом деле, из
.
В самом деле, из 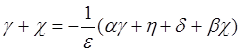 следует
следует ![]() , что как уже было установлено ранее,
выполняется при Q = 0.
, что как уже было установлено ранее,
выполняется при Q = 0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.