Зображення за Лапласом вхідного сигналу ![]() :
:
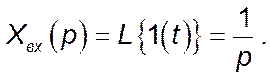
Звідси зображення за Лапласом вихідного сигналу:
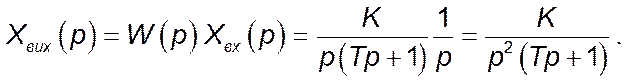
Оригінал вихідного сигналу можна знайти, виходячи з наступних міркувань. Судячи з наведеного виразу функції передачі для даної ланки, її вихідний сигнал дорівнює інтегралу вихідного сигналу простої аперіодичної ланки при одиночному стрибкоподібному сигналі на вході, тобто:
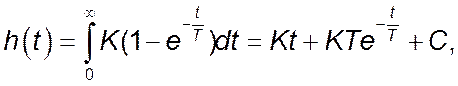
де С – стала інтегрування, яка визначається початковими умовами.
При t = 0 h(t) = 0, тому С = - KT. Таким чином
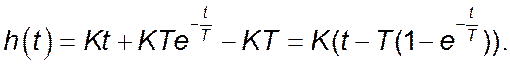
Перехідна характеристика зображена на рисунку. Вона наближається до
прямої лінії, яка зміщена відносно початку координат на відстань T і іде під кутом ![]() до
осі абсцис.
до
осі абсцис.
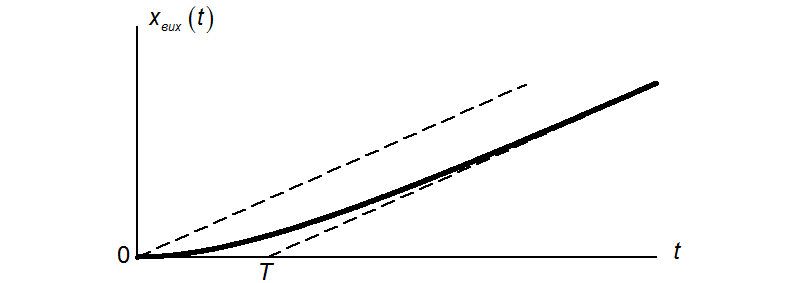
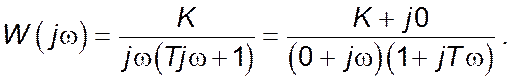
Амплітудно-частотна характеристика ![]() :
:
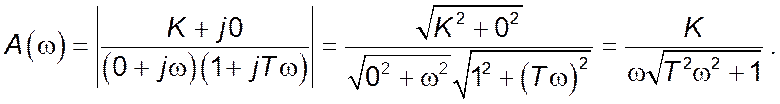
Фазово-частотна характеристика ![]() :
:
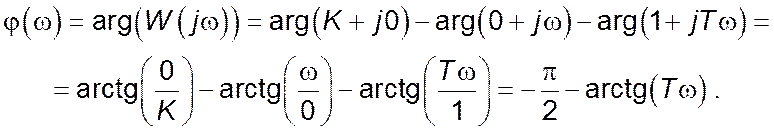
Дійсна частина комплексного коефіцієнту передачі:
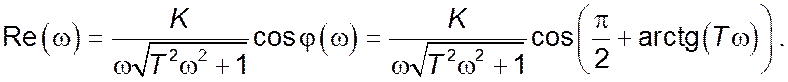
Уявна частина комплексного коефіцієнту передачі:
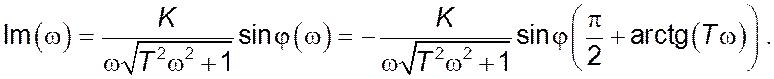 )
)
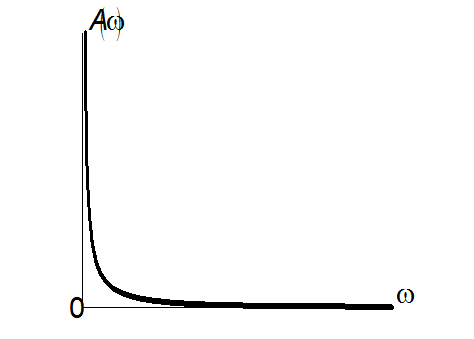 Амплітудно-частотна
характеристика
Амплітудно-частотна
характеристика 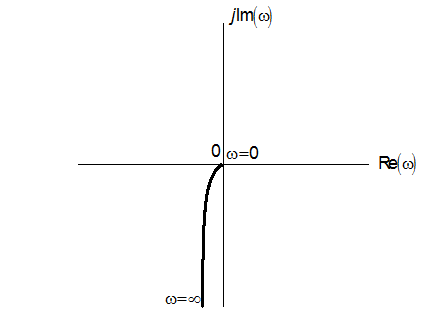
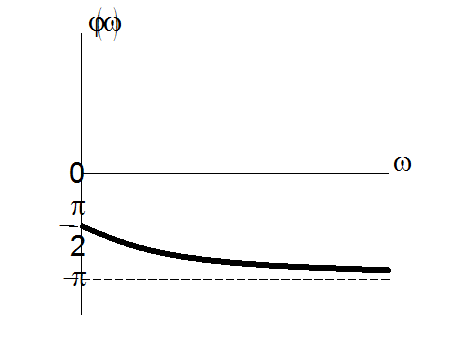 Фазово-частотна
характеристика
Фазово-частотна
характеристика
Амплітудно-фазова частотна характеристика
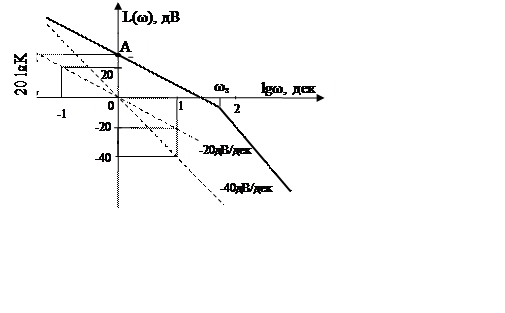
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
аперіодичної інтегруючої ланки описується виразом L(ω) = 20lgK-20lgω-20lg![]() , являє собою
ламану лінію, яка проходить через точку А[0; 20lgK] під кутом -20 дВ/дек , при частоті
, являє собою
ламану лінію, яка проходить через точку А[0; 20lgK] під кутом -20 дВ/дек , при частоті 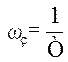 зменшує
кут нахилу ще на 20 дВ/дек і при високих частотах має кут нахилу -40 дВ/дек
зменшує
кут нахилу ще на 20 дВ/дек і при високих частотах має кут нахилу -40 дВ/дек
Проста аперіодична ланка другого порядку
Рівняння динаміки в операційній формі і функція передачі простої аперіодичної ланки 2 – го порядку:
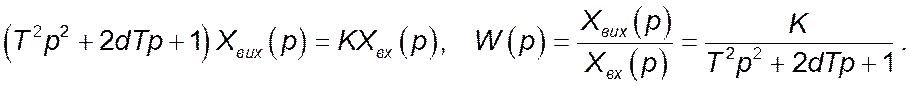
В наведених формулах для цієї ланки показник затухання ![]() . При таких умовах
корені характеристичного рівняння Т2р2+2dТр+1=0 мають дійсний характер, саме тому
поліном 2 – го порядку лівої частини рівняння динаміки може бути представлений у
вигляді добутку двох двочленів, тобто:
. При таких умовах
корені характеристичного рівняння Т2р2+2dТр+1=0 мають дійсний характер, саме тому
поліном 2 – го порядку лівої частини рівняння динаміки може бути представлений у
вигляді добутку двох двочленів, тобто:
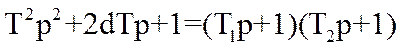 ,
,
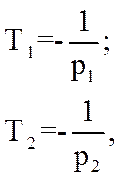
де Т1 і Т2 – сталі часу, а р1 і р2 – корені характеристичного рівняння:
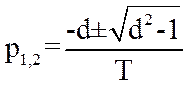 .
.
Отже, функція передачі цієї ланки може бути записана так:
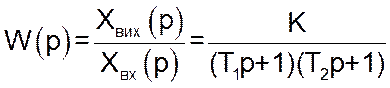
Зображення за Лапласом вхідного сигналу ![]() :
:
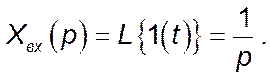
Звідси зображення за Лапласом вихідного сигналу:
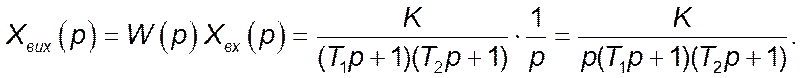
Оригінал вихідного сигналу можна знайти, користуючись теоремою розкладення
в випадку однократного нульового полюса (для коливальної ланки необхідно
виконання умови ![]() ):
):
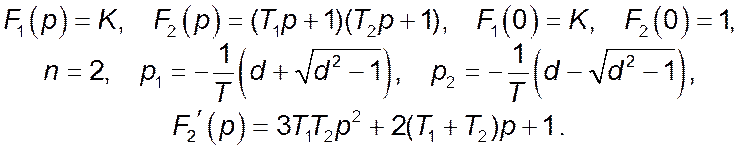
Користуючись теоремою розкладення, можна визначити перехідну функцію простої аперіодичної ланки 2 – го порядку:
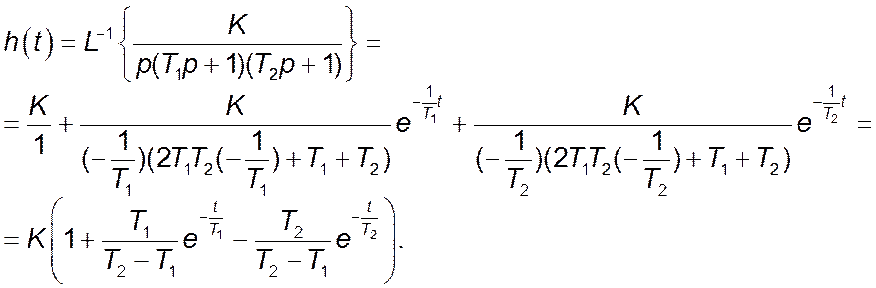
Перехідна характеристика зображена на рисунку. Вона нагадує вигляд перехідної характеристики простої аперіодичної ланки першого порядку з деякою відмінністю, яка полягає у тому , що максимум швидкості монотонного наростання сигналу припадає не на нульовий момент часу, а через деякий інтервал.
 |
Виконавши заміну p на ![]() , отримаємо
комплексний коефіцієнт передачі:
, отримаємо
комплексний коефіцієнт передачі:
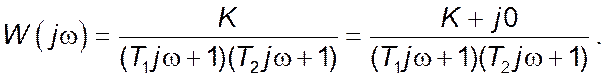
Амплітудно-частотна характеристика ![]() :
:
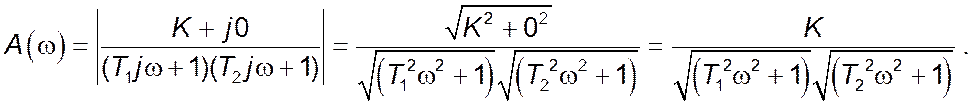
Фазово-частотна характеристика ![]() :
:
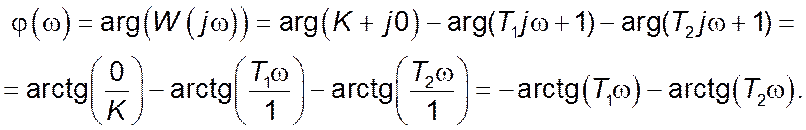
Дійсна частина комплексного коефіцієнту передачі:
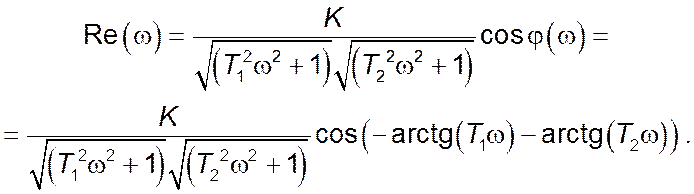
Уявна частина комплексного коефіцієнту передачі:
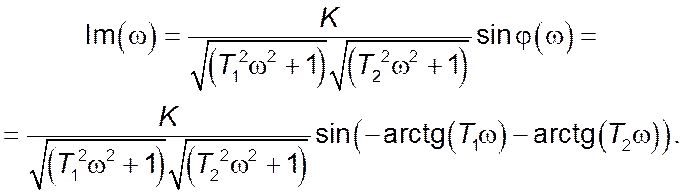
 |
 |
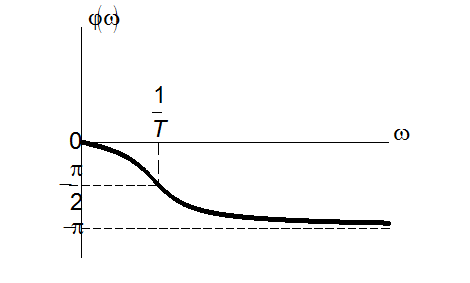
Фазово-частотна характеристика
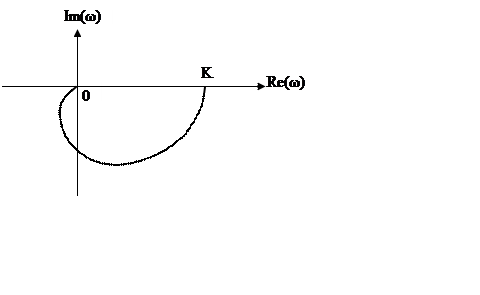
Амплітудно-фазова частотна характеристика
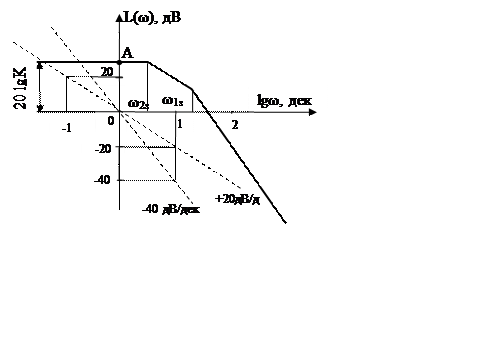
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ) цієї ланки описується виразом
L(ω) = 20lgK-20lg![]() -20lg
-20lg![]() ,
являє собою ламану лінію, яка горизонтально перетинає точку А[0; 20lgK]. Якщо Т2>Т1, то ω2з<ω1з,
тому ЛАЧХ L(ω) змінює кут нахилу на
-20 дВ/дек спочатку при частоті
,
являє собою ламану лінію, яка горизонтально перетинає точку А[0; 20lgK]. Якщо Т2>Т1, то ω2з<ω1з,
тому ЛАЧХ L(ω) змінює кут нахилу на
-20 дВ/дек спочатку при частоті 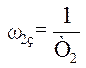 ,
а потім ще раз зменшує кут нахилу на-20 дВ/дек при частоті
,
а потім ще раз зменшує кут нахилу на-20 дВ/дек при частоті 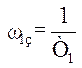 . На високих частотах кут нахилу
залишається -40 дВ/дек.
. На високих частотах кут нахилу
залишається -40 дВ/дек.
Проста коливальна ланка
Рівняння динаміки в операційній формі і функція передачі простої коливальної ланки:
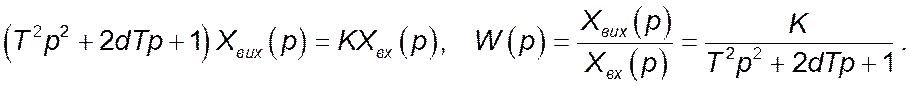
Зображення за Лапласом вхідного сигналу ![]() :
:
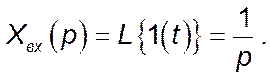
Звідси зображення за Лапласом вихідного сигналу:
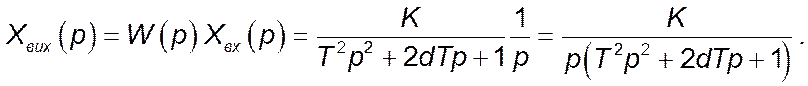
Оригінал вихідного сигналу можна знайти, користуючись теоремою розкладення
в випадку однократного нульового полюса (для коливальної ланки необхідно
виконання умови ![]() ):
):
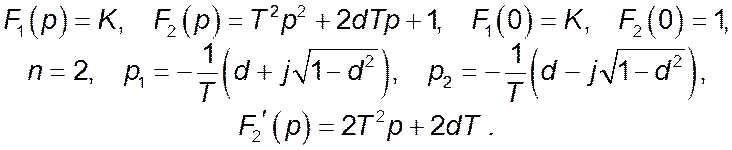
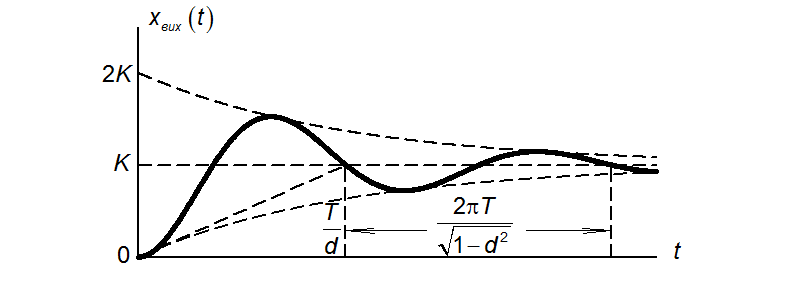
Перехідна функція має вигляд
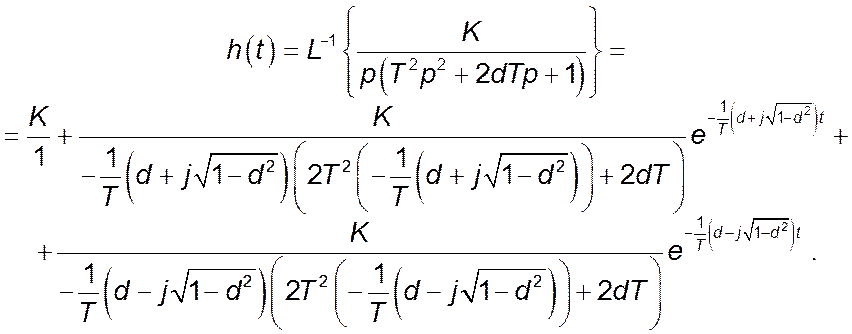
Після необхідних математичних спрощень отримаємо остаточний вигляд перехідної функції:
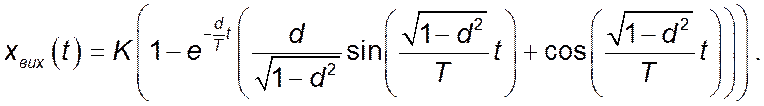
Перехідна характеристика зображена на рисунку. Вона має явно виражений коливальний характер і наближається в усталеному режимі до значення K.
Виконавши заміну p на ![]() , отримаємо
комплексний коефіцієнт передачі:
, отримаємо
комплексний коефіцієнт передачі:
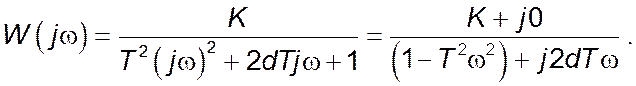
Амплітудно-частотна характеристика ![]() :
:
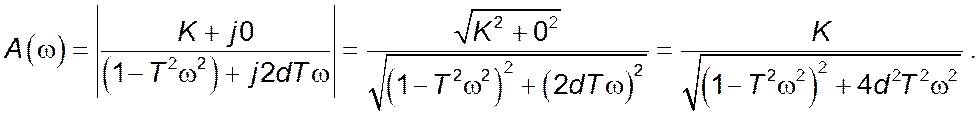
Фазово-частотна характеристика ![]() :
:
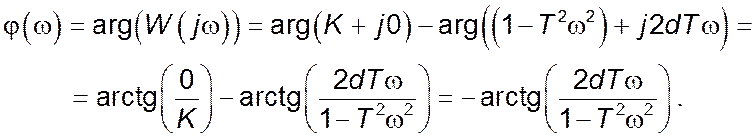
Дійсна частина комплексного коефіцієнту передачі:
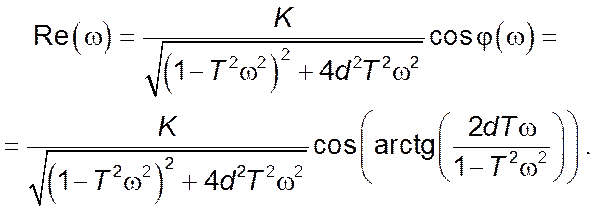
Уявна частина комплексного коефіцієнту передачі:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.