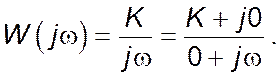
Амплітудно-частотна характеристика ![]() може
бути побудована за виразом
може
бути побудована за виразом 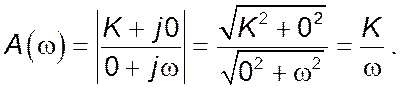
Фазово-частотну характеристику ![]() можна
побудувати за виразом:
можна
побудувати за виразом:
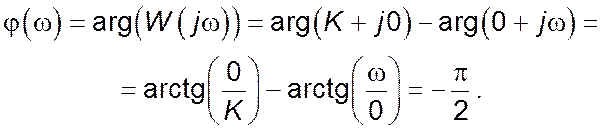
Дійсна частина комплексного коефіцієнту передачі:
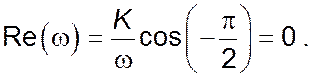
Уявна частина комплексного коефіцієнту передачі:
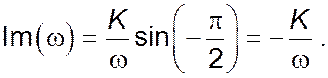
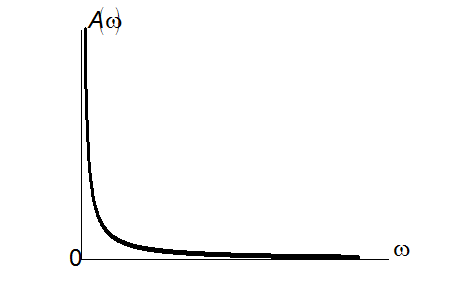
Амплітудно-частотна характеристика 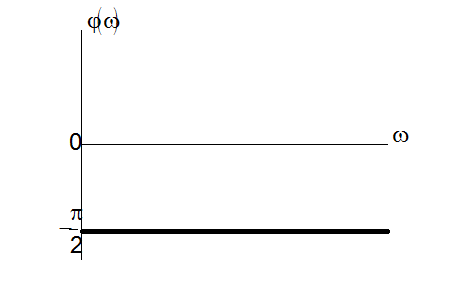
Фазово-частотна характеристика
 |
 |
||
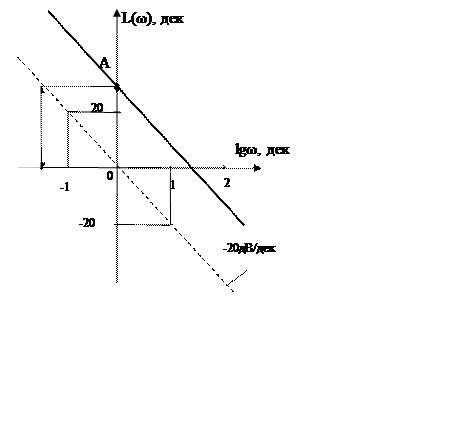
Логарифмічна амплітудно-частотна характеристика
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ) інтегруючої ланки описується виразом L(ω) = 20lgK-20lgω, являє собою пряму лінію, яка проходить через точку А[0; 20lgK] під кутом -20 дВ/дек.
Проста аперіодична ланка 1 – го порядку
Рівняння динаміки в операційній формі і функція передачі простої аперіодичної ланки:
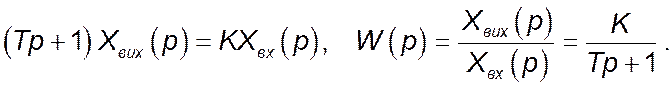
Зображення за Лапласом вхідного сигналу ![]() :
:
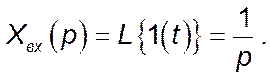
Звідси зображення за Лапласом вихідного сигналу:
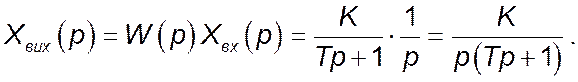 (1)
(1)
Оригінал вихідного сигналу можна знайти, користуючись теоремою розкладення в випадку однократного нульового полюса:
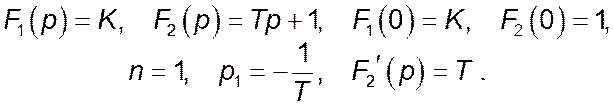 (2)
(2)
Отже, перехідна функція має вигляд
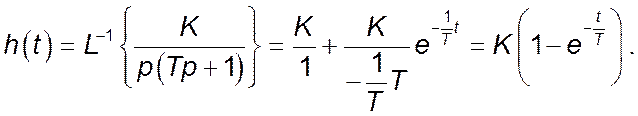 (3)
(3)
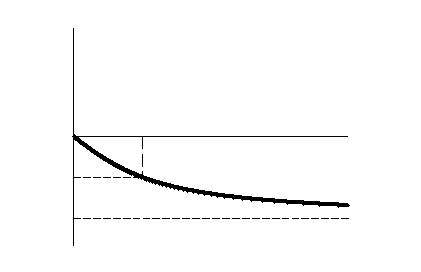
Перехідна характеристика зображена на рисунку 3.
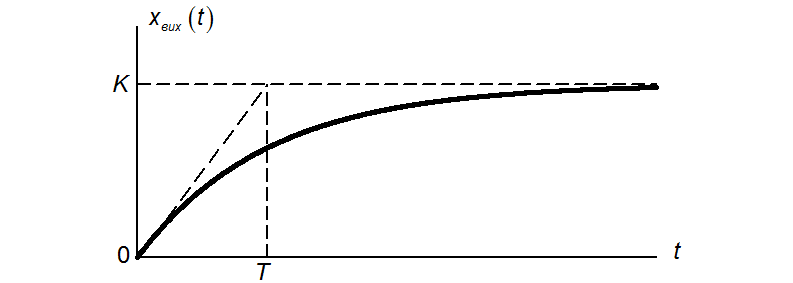
При ![]() перехідна характеристика досягає
приблизно 63,2 % від значення K, при
перехідна характеристика досягає
приблизно 63,2 % від значення K, при ![]() приблизно 86,5 %, при
приблизно 86,5 %, при ![]() приблизно 95,0 %, при
приблизно 95,0 %, при ![]() приблизно 98,2 %.
приблизно 98,2 %.
Виконавши заміну p на ![]() , отримаємо
комплексний коефіцієнт передачі:
, отримаємо
комплексний коефіцієнт передачі:
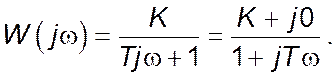
Амплітудно-частотна характеристика ![]() може
бути побудована за виразом:
може
бути побудована за виразом:
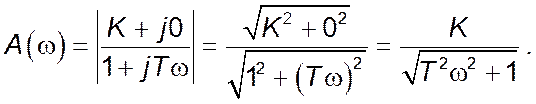
Фазово-частотна характеристика ![]() може
бути побудована за виразом:
може
бути побудована за виразом:
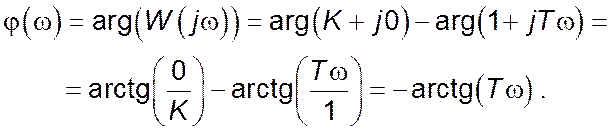
Дійсна частина комплексного коефіцієнту передачі:
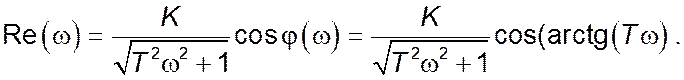
Уявна частина комплексного коефіцієнту передачі:
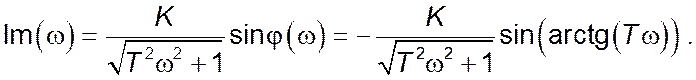
 |
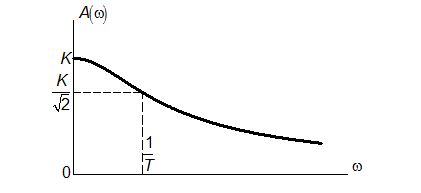
Амплітудно-частотна характеристика Фазова-частотна характеристика
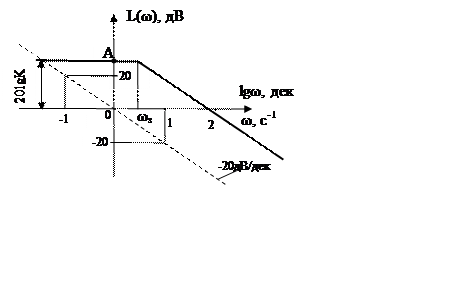
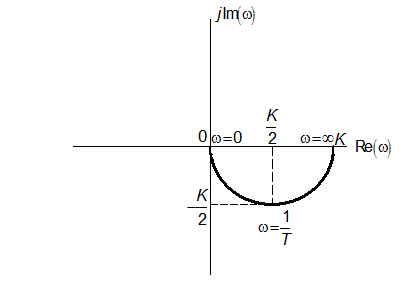
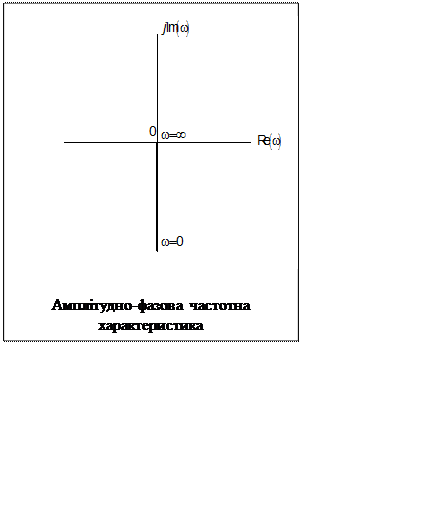
Амплітудно-фазова частотна характеристика
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
За формою АФЧХ простої аперіодичної ланки являє собою півколо радіусом, який дорівнює К/2.
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
простої аперіодичної ланки 1 –го порядку описується виразом
L(ω) = 20lgK-20lg![]() , являє собою
ламану лінію, яка проходить горизонтально через точку А[0; 20lgK], а при чаcтоті
, являє собою
ламану лінію, яка проходить горизонтально через точку А[0; 20lgK], а при чаcтоті 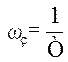 змінює кут нахилу на -20
дВ/дек.
змінює кут нахилу на -20
дВ/дек.
Аперіодична диференціююча ланка
Рівняння динаміки в операційній формі і функція передачі аперіодичної диференціюючої ланки:
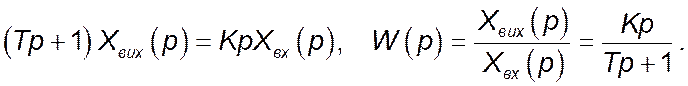
Зображення за Лапласом вхідного сигналу ![]() :
:
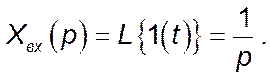
Звідси зображення за Лапласом вихідного сигналу:
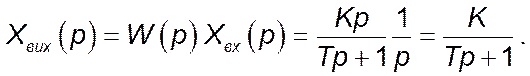
Оригінал вихідного сигналу можна знайти, користуючись теоремою розкладення в випадку простих полюсів:
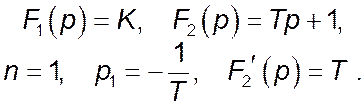
Отже, перехідна функція має вигляд
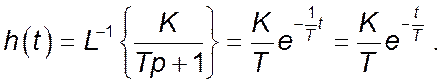
Перехідна характеристика зображена на рисунку.
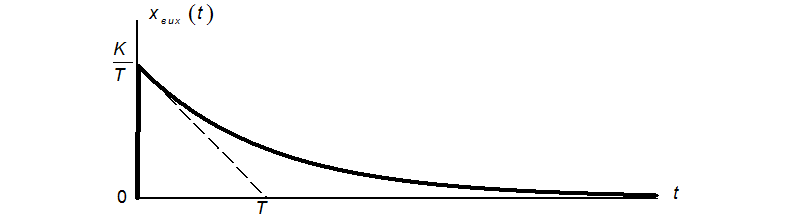
При ![]() перехідна характеристика досягає
приблизно 36,8 % від значення
перехідна характеристика досягає
приблизно 36,8 % від значення ![]() , при
, при ![]() - 13,5 %, при
- 13,5 %, при ![]() - 5,0 %, при
- 5,0 %, при ![]() - 1,8 %.
- 1,8 %.
Виконавши заміну p на ![]() , отримаємо
комплексний коефіцієнт передачі:
, отримаємо
комплексний коефіцієнт передачі:
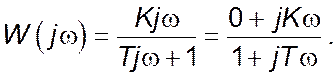
Амплітудно-частотна характеристика ![]() може
бути побудована за виразом:
може
бути побудована за виразом:
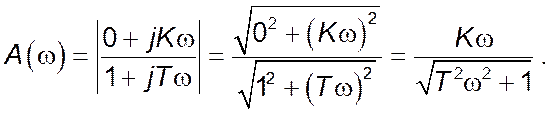
Фазово-частотна характеристика ![]() може
бути побудована за виразом:
може
бути побудована за виразом:
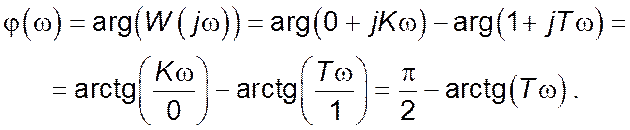
Дійсна частина комплексного коефіцієнту передачі:
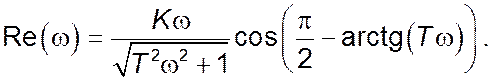
Уявна частина комплексного коефіцієнту передачі:
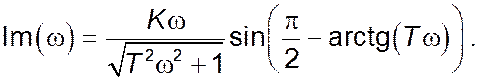
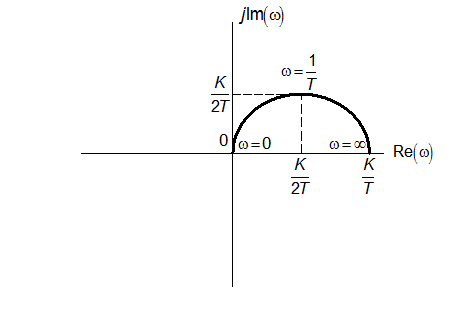 |
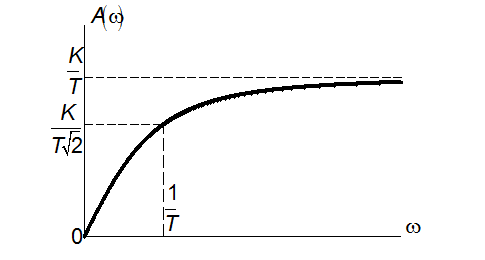 Амплітудно-частотна
характеристика
Амплітудно-частотна
характеристика 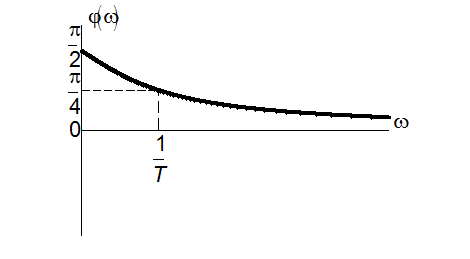
Фазово-частотна характеристика
 |
Амплітудно-фазова частотна характеристика
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
Як і для АФЧХ простої аперіодичної ланки, амплітудно-фазова частотна характеристика аперіодичної диференціюючої ланки за формою являє собою півколо, але з радіусом, який дорівнює К/2Т.
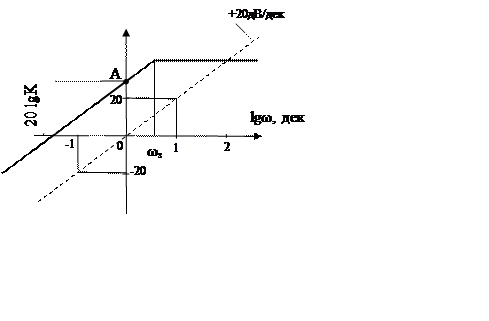
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
аперіодичної диференціюючої ланки описується виразом L(ω) = 20lgKω-20lg![]() , являє собою
ламану лінію, яка проходить через точку А[0; 20lgK] під кутом +20 дВ/дек , при чаcтоті
, являє собою
ламану лінію, яка проходить через точку А[0; 20lgK] під кутом +20 дВ/дек , при чаcтоті 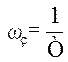 зменшує кут нахилу на 20
дВ/дек і надалі стає горизонтальною.
зменшує кут нахилу на 20
дВ/дек і надалі стає горизонтальною.
Аперіодична інтегруюча ланка
Рівняння динаміки в операційній формі і функція передачі аперіодичної інтегруючої ланки:
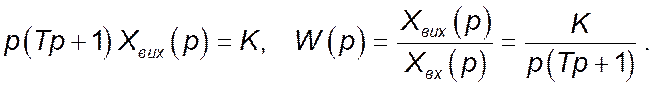
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.