Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 4

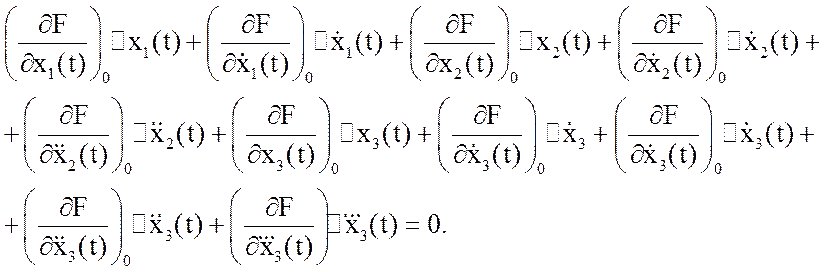
Це рівняння, як і вихідне, описує той же динамічний процес у тій же системі керування. Всі часткові похідні являють собою постійні коефіцієнти, оскільки в них замість змінних підставлені їхні числові значення в сталому режимі. По суті, це рівняння являє собою суму перших ступенів різних змінних з відповідними коефіцієнтами. Таке рівняння є лінійним.

Відмінність його від вихідного нелінійного полягає в наступному:

Лінійне рівняння є наближеним , оскільки воно отримане в результаті відкидання в розкладанні Тейлора членів вищого порядку малості.

Невідомими функціями часу є не самі змінні х₁(t),х₂(t),х₃(t) і їхні похідні, а прирісти Δх₁(t), Δх₂(t), Δх₃(t) і т.д. Таке рівняння називається рівнянням у приростах (у варіаціях).

З отриманого виразу видно, що лінеаризація зводиться до одержання повного диференціала функції при заданих сталих значеннях змінних. Це можливо лише для функцій, що диференціюються, тобто таких, які у всіх точках мають кінцеві похідні. Функції, що не диференціюються, в такий спосіб лінеаризовувати не можна, існують інші способи лінеаризації, які будуть розглянуті далі.

Форми запису диференціальних рівнянь. Функція передачі.

Розглянемо простий варіант, у якому є одна вхідна величина х₁ й одна вихідна х₂.

Припустимо, що вихідне рівняння має вигляд:

.

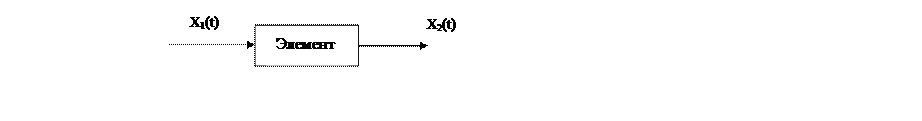У лінеаризованому вигляді:

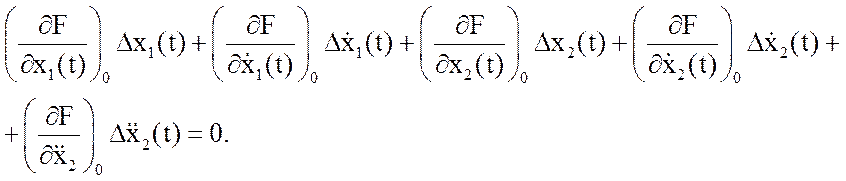
Уведемо позначення постійних коефіцієнтів:

.

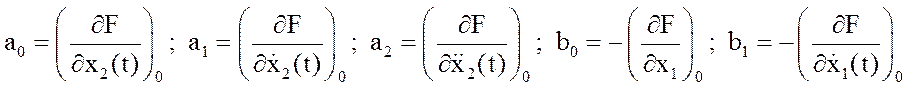Після цього перейдемо до стандартної форми запису. Пам’ятаючи завжди, що рівняння динаміки записано у приростах, для більш стислої форми відкинемо позначку Δ:

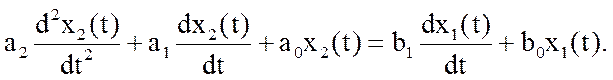
Маючи на увазі, що х₁ є вхідною величиною, а х₂  – вихідною, у загальному виді рівняння може бути записано:

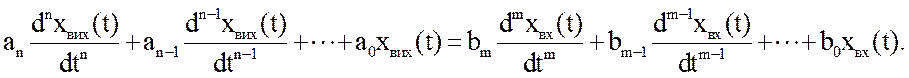
Диференціальне рівняння може бути записане в операторній формі:

де р =  – оператор диференціювання.

Операторна форма не міняє його сутності, воно залишається диференціальним. У сталому режимі, коли х_вх = const, х_вих = const , p=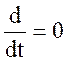 , одержуємо рівняння статики:

а₀х_вих = b₀х_вх,

звідки:

,

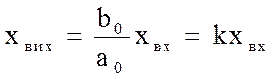де k = 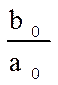– коефіцієнт передачі (посилення), що визначає крутість статичної характеристики.

Аналітичне рішення диференціальних рівнянь, особливо високого порядку, пов'язане з певними математичними труднощами, тому для полегшення цього завдання використовують спеціальні перетворення (наприклад, Лапласа або Карсона-Хевісайда), які дозволяють перейти від диференціальних рівнянь до алгебраїчних. При цьому у вихідних рівняннях здійснюється заміна реальних змінних і їхніх похідних відповідними зображеннями.

У вихідних рівняннях незалежної змінною є час t, а в їх зображеннях - комплексна змінна p=c+jω.

Пряме перетворення Лапласа, тобто перехід від оригіналу до зображення здійснюється за допомогою інтеграла Лапласа:

.

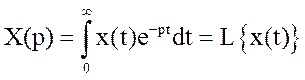Для багатьох функцій існують таблиці перетворень Лапласа (див. відповідну таблицю).

Формули прямого і оберненого перетворення за Лапласом

№ п/п	Оригінал	Зображення
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Практичний перехід від диференціальних рівнянь до їхніх зображень по Лапласу здійснюється без яких-небудь обчислень. Формально, при нульових початкових умовах, перетворення здійснюється шляхом заміни оригіналів функції х(t) їхніми зображеннями Х(р), а символів диференціювання 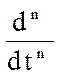 позначенням оператора Лапласа рⁿ. Операція диференціювання оригіналу функції відповідає операції множення її зображення на комплексне число р:

,

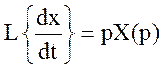 операція інтегрування оригіналу функції відповідає операції поділу її зображення на р:

.

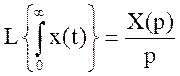З огляду на вищесказане, запишемо вихідне рівняння, використовуючи перетворення Лапласа:

.

Така форма запису називається операційною формою. Рівняння в операційній формі по природі є алгебраїчним, рішенням такого рівняння є зображення змінної у часі величини, а не сама величина.

Рішенням алгебраїчного рівняння є зображення по Лапласу вихідної величини:

.

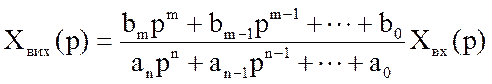Для визначення оригіналу можна скористатися або таблицями зворотних перетворень, або шляхом обчислення відповідного інтеграла зворотного перетворення Лапласа:

.

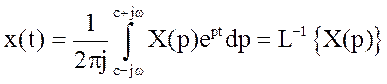Дріб, що знаходиться в правій частині зображення по Лапласу вихідної величини, являє собою відношення зображень вихідної і вхідної величин (при нульових початкових умовах), називається функцією передачі W(p).

.

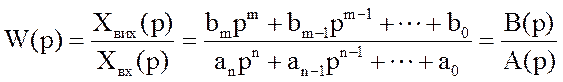Знаменник функції передачі прирівняний до нуля називається характеристичним рівнянням:

,

воно визначає перехідну складову протікання процесу. У сталому режимі, тобто при р=0, функція передачі W(0) чисельно дорівнює коефіцієнту передачі k:

.

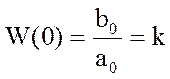Статичні і динамічні і характеристики.

Рівняння статикивідбиває в аналітичній формі зв'язок між вихідною й вхідною величинами в сталому режимі, яке можна отримати шляхом підстановки в рівняння динаміки значення р=0.

Графічне зображення залежності вихідної величини від вхідної в сталому режиміназивається статичною характеристикою.

Перехідною функцією h(t) називається аналітичний опис зміни вихідної величини у часі при одиничній стрибкоподібній зміні вхідної величини при нульових початкових умовах. Перехідна функція відбиває реакцію елементу або системи в цілому на одиничний ступінчастий вплив при нульових початкових умовах, що по суті являє собою перехідний процес, який виникає в елементі при одиничному стрибку сигналу на вході (х_вх(t) = 0 при t0;  х_вх(t) = 1 при t > 0).

Перехідна функція може бути отримана шляхом рішення диференціального рівняння класичним методом або, використовуючи перетворення Лапласа, операційним методом.