Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 22

Підставивши, у відповідне рівняння одержимо на площині А₁,А2 крапку С. У цій крапці виконується умова  

Всі три корені отриманого рівняння в крапці З,  тобто є речовинними й рівними між собою.

У загальному випадку в системі 3-го порядку корінь характеристичного рівняння можуть бути:

Рівними речовинними (у розглянутій крапці З).

Різними речовинними.

Один речовинний і два комплексних сполучених.

У площині коефіцієнтів характеристичного рівняння А₂, А₁ границя області, для якої корінь будуть різними речовинними, визначаються з умови рівності нулю дискримінанта.

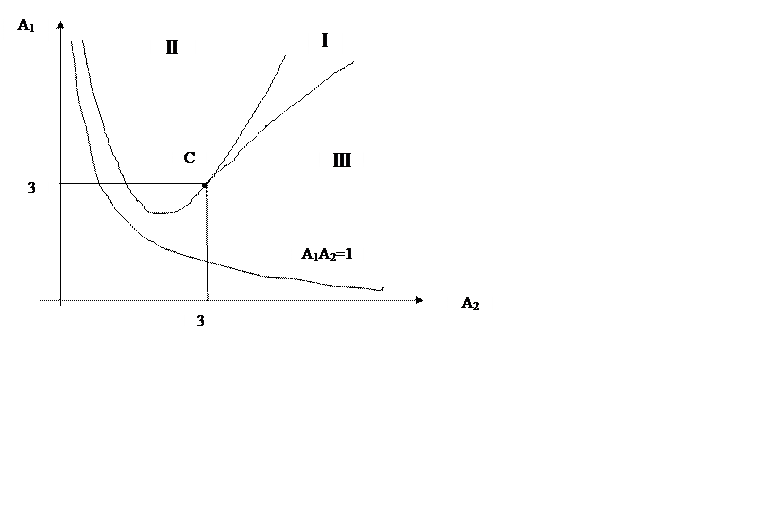
Підставляючи в зазначене вираження різні значення А₁ й А₂, одержимо криві РЄ й CF. Усередині області (I), обмежене кривій ЕCF дискримінант позитивний, всі корінь для неї речовинні. За межами цієї області дискримінант негативний, тому один корінь речовинний, а два інших - комплексні сполучені.

Варто нагадати, що якщо в площині розподілу корінь найближчим до мнимої осі буде речовинний корінь, ступінь стійкості  аперіодична, якщо ж ближче всіх розташована пара комплексних сполучених корінь, то ступінь стійкості коливальна. Отже, істотне значення має взаиморасположение речовинного й пари комплексних сполучених корінь.

Розглянемо граничний випадок, коли речовинний і пари комплексних корінь   перебувають на тому самому відстані від мнимої осі,

 т. е.     

 У цьому випадку характеристичне рівняння буде мати вигляд:

Cледовательно: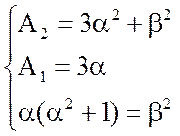

Вирішуючи спільно отриману систему рівнянь:

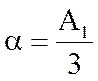
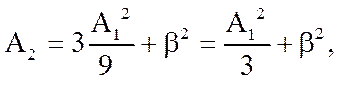
 звідки

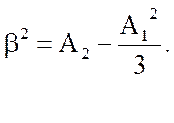
Підставляючи значення   й   в 3-і рівняння системи

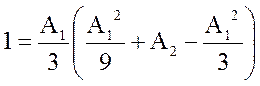
В остаточному підсумку одержимо рівняння:

У площині коефіцієнтів А₂,А₁ це рівняння відображається кубічною параболою ВР поділяюча область стійкості поза межами площини обмеженій кривій ЕС, на дві області, одна йз яких (II) відповідає тому розташуванню корінь, у якому найближчим до мнимої осі є речовинний корінь, а інша (область III) відповідає розташуванню корінь, у якому найближчими є пара комплексних корінь.

Таким чином, Диаграммма Вышнеградского, що представляє собою сукупність кривих ВР, РЄ, CF розбиває область стійкості площини коефіцієнтів А₂,А₁ системи 3-го порядку на три подобласти (I, II, III), кожної з яких відповідають певний вид корінь характеристичного керування і їх взаиморасположение на комплексній площині корінь.

Взаиморасположение корінь і вид перехідного процеса для кожної з областей представлені на малюнках:

Область Й:

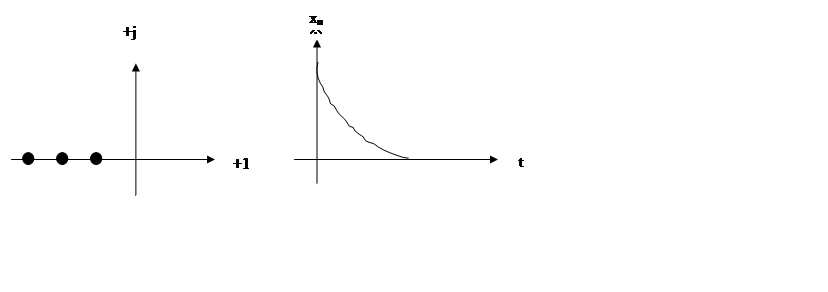
Область II:

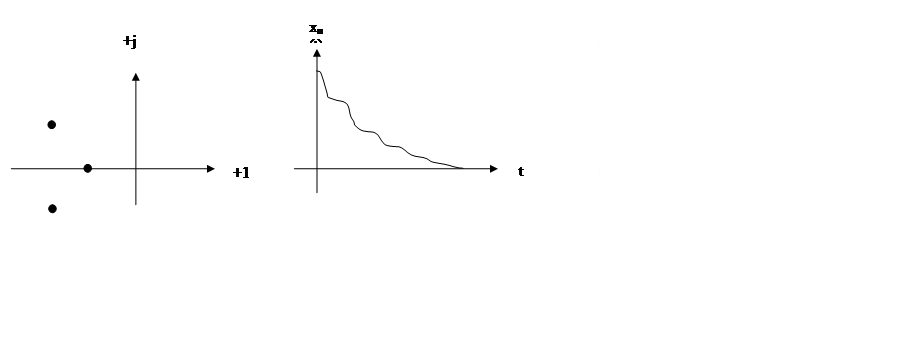
Область III:

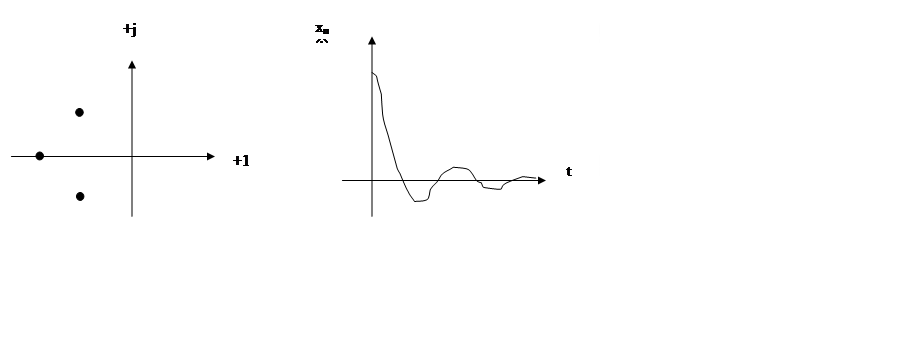
По діаграмі Вышнеградского можна судити лише про характер перехідного процеса, але не можна висловити певного судження про інші характеристики (часу процесу керування t_у, загасанні, і т.д.).

У зв'язку із цим діаграма була вдосконалена нанесенням на неї додаткових ліній нормованого ступеня стійкості h_o і ступеня колебательности  μ.

Визначивши значення безрозмірних коефіцієнтів А₂,А₁ по відповідних формулах і скориставшись діаграмою Вышнеградского, доповненої лініями h_o й  μ, неважко визначити ступінь стійкості й ступінь колебательности.

При цьому ступінь стійкості h й її нормоване значення h_o зв'язані залежністю 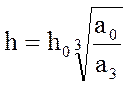      (приводиться без доказу, більш докладно див.  стор. 215-223).

Частотні оцінки якості керування

Оцінки якості по частотних властивостях замкнутих систем.

Під частотними оцінками якості будемо розуміти такі оцінки, які базуються на деяких частотних властивостях як розімкнутих, так і замкнутих систем.

Частотні оцінки замкнутих систем найбільше повно розроблені відносно оцінки запасу стійкості. Запас стійкості може бути виражений різним способом, залежно від того, яким критерієм скористатися. Так, наприклад, якщо використається критерій стійкості Михайлова, запас стійкості відповідає радіусу окружності «заборонної зони», у яку не повинен заходити годограф Михайлова.

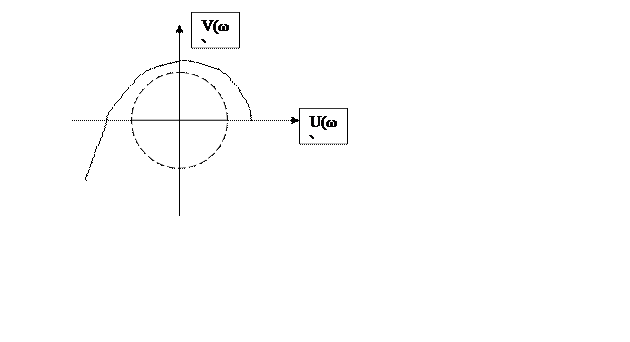Оцінка якості керування по ВЧХ замкнутої системи

Будемо думати, що перехідний процес у САУ викликаний стрибком впливу, що задає, в. У загальному випадку речовинна частотна характеристика (ВЧХ) Р(ω) може мати вигляд:

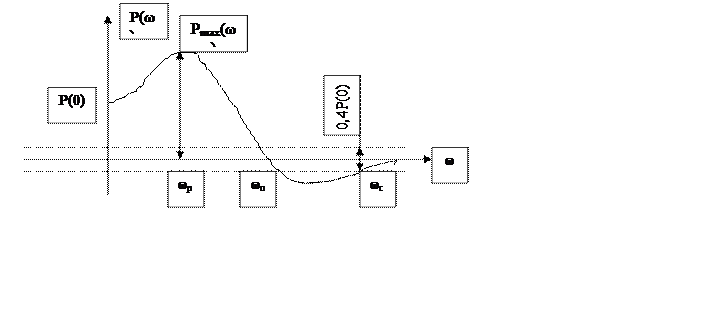
Інтервал частот , у якому , називається інтервалом позитивності, інтервал частот  називається інтервалом істотних частот, якщо при    стає менше деякої досить малої величини .

Впливом іншої частини ВЧХ (при ) на якість процесу керування можна зневажити. Якщо ж при ω>ω_п виявляється, що < ,те при оцінці якості процесу керування можна брати до уваги тільки інтервал позитивності .

Сформулюємо ряд положень, що визначають взаємозв'язок ВЧХ і перехідної характеристики САУ.

Якщо ВЧХ P(?) обмежена по модулі на всьому діапазоні істотних частот, то перехідна характеристика також обмежена по модулі.

Якщо P(ω) при деякій частоті ω_p необмежено зростає, то в системі виникають незатухаючі коливання із частотою ω_p.

Якщо ВЧХ P(ω)  може бути представлена у вигляді суми окремих характеристик 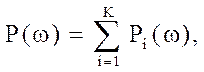 то перехідний процес відповідний  P(ω) може бути отриманий як сума перехідних процесов для кожного    

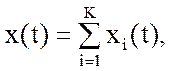
 де 

.

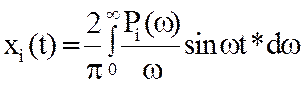Якщо ВЧХ зв'язані співвідношенням то відповідні їм перехідні процеси будуть також зв'язані співвідношенням

Ніж ширше ВЧХ (чим більшу площу вона займає), тим швидше загасає перехідний процес.

Сталого значення керованої величини дорівнює значенню Р(ω) при нульовій частоті, тобто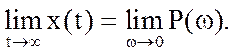

Початкове значення перехідної характеристики дорівнює кінцевому значенню ВЧХ 

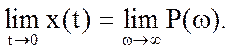
Якщо ВЧХ є позитивною незростаючою функцією, тобто  >0; і 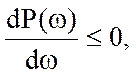  при 0<ω<ω_c, те перерегулювання σ,% не перевищує 18% від сталого значення .

Якщо ВЧХ являє собою монотонну убутну функцію (тобто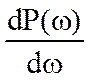 <0) в області істотних частот, то перехідний процес також монотонним, без перерегулювання. Час перехідного процесу, тобто час керування,  > .

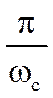У випадку незростаючої ВЧХ час керування  укладений у межах    < < .

Перехідний процес буде коливальним, якщо є значення P(?)>P(0).