Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 15

Логарифмічний критерій стійкості.

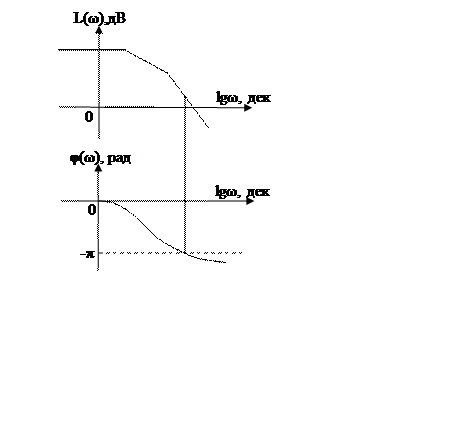
У відповідності до критерію стійкості Найквіста, в стійких замкнених системах при значенні аргументу АФЧХ розімкненої системи φ(ω)=- π, значення модуля W(jω) повинне бути менше одиниці, тобто А(ω)<1, а логарифмічна амплітудно-частотна характеристика  розімкненої системи (ЛАЧХ) L(ω)=20 lg А(ω)<0.

Якщо побудувати ЛАЧХ і ЛФЧХ для розімкненої системи, то неважко встановити їх взаємозв’язок, який забезпечує стійкість системи автоматичного керування у замкненому стані.

Будемо розглядати лише системи, які є стійкими у розімкненому стані.

На першому рисунку при частоті, при якій значення ЛФЧХ φ(ω) стає рівним –π, значення ЛАЧХ L(ω)>0. Це означає, що АФЧХ розімкненої системи перетинає дійсну вісь в інтервалі значень за межами , тобто охоплює критичну точку С, тому замкнена система буде нестійкою.

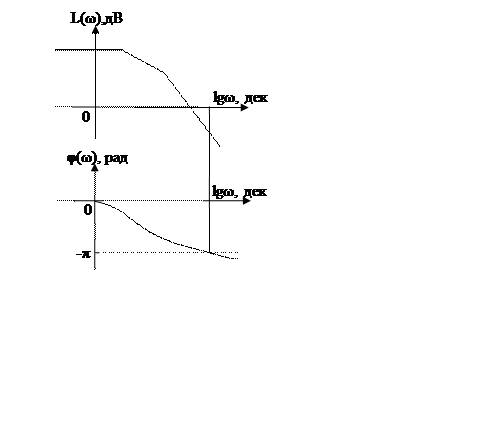На другому рисунку при  частоті, при якій ЛФЧХ φ(ω) відповідає тій же умові, ЛАЧХ L(ω)<0, тому АФЧХ розімкненої системи перетинає дійсну вісь в інтервалі значень від (-1) до 0, що відповідає стійкості замкненої системи керування.

Замкнена система керування буде абсолютно стійкою, якщо при частоті, при якій ЛФЧХ перетинає горизонтальну лінію –π, ЛФЧХ має додатне значення.

У випадку умовної стійкості вигляд ЛФЧХ має інший вигляд:

Частота, при якій ЛАЧХ перетинає вісь абсцис, називають частотою зрізу ω_зр, формулювання логарифмічного критерію стійкості змінюється:

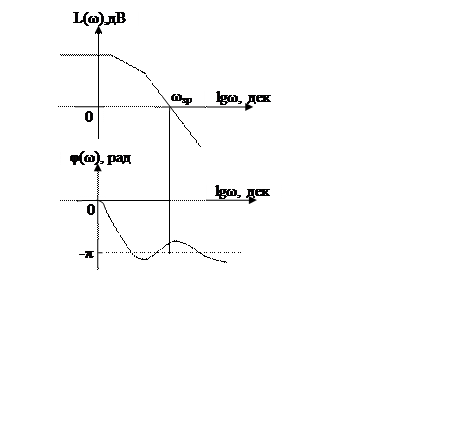Умовна стійкість забезпечується, якщо кількість перетинів ЛФЧХ φ(ω)значень –π до частоти зрізу ω_зр парне.

Нестійкі системи у розімкненому стані не розглядаються.

Особливості стійкості систем з запізненням.

При наявності в системі автоматичного керування елементів запізнення виникає  необхідність визначення граничних значень часу запізнення, при яких система втрачає стійкість, оскільки такі ланки є джерелом збурень, що в істотній мірі впливають на фазові зсуви сигналів, отже на стійкість.

Розглянемо розімкнену систему автоматичного керування, яка містить ланку чистого (транспортного) запізнення:

Функція передачі такої системи

W(p) = W_o(p) ∙W_τ(p)= W_o(p) e^-pτ,

де W_о(p) – функція передачі частини системи без запізнення,

W_τ(p)=e^-pτ – функція  передачі ланки чистого запізнення,

τ – час запізнення.

Функція передачі замкненої системи має вигляд:

Φ(р)=.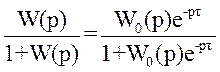

Характеристичне рівняння замкненої системи:

=0.

Таким рівнянням можна користуватися для досліджень стійкості системи за допомогою будь-яких критеріїв. Але при аналізі характеристичного рівняння такого вигляду виникають певні математичні труднощі, тому більш зручним є використання критерію стійкості Найквіста, для якого не потрібно визначати функцію передачі для замкненої системи.

Комплексний коефіцієнт передачі розімкненої системи при наявності елемента чистого запізнення:

W(jω) = W_o(jω) ∙W_τ(jω)= А_o(ω) e^jφ(ω) А_τ(ω) e^-jωτ,

а оскільки значення амплітудно-частотної характеристики ланки чистого запізнення А_τ(ω)  для всіх частот дорівнює одиниці, то:

W(jω) = А_o(ω) e^{j(φ(ω)-ωτ)}.

Аналізуючи отриманий результат,  можна зробити висновок, що наявність ланки чистого запізнення не впливає на модуль вектора АФЧХ, але змінює фазовий зсув в напрямку руху годинникової стрілки на кут, що дорівнює –ωτ.

Розглянемо випадок, коли АФЧХ розімкненої системи перетинає коло одиничного радіуса в одній точці.

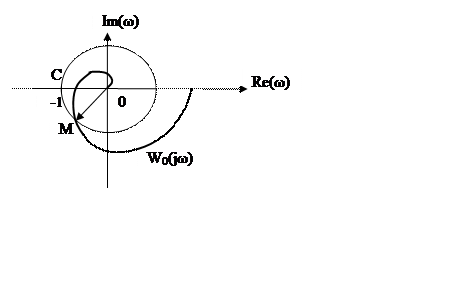
Позначимо літерою М точку перетину АФЧХ розімкненої частини системи W_o(jω), яка не має запізнення з колом одиничного радіуса. Ця точка відповідає конкретній частоті ω_м, при якій значення ФЧХ дорівнює φ(ω_м). Наявність в системі ланки чистого запізнення повертає вектор ОМ в напрямку руху годинникової стрілки на кут, величина якого залежить від значення часу запізнення. При деякому значенні цього часу τ_кр можливе виконання рівності:

φ(ω_м)- ω_мτ_кр=-π,

звідки                                                                  τ_кр=.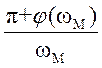

Побудова областей стійкості. D-розбивка

            При дослідженні САУ часто виникає необхідність встановити вплив параметрів системи на її стійкість. Для рішення цього завдання виконують побудову областей стійкості, тобто, областей значень параметрів при яких система є стійкою.

            Розрізняють побудову областей стійкості в площині значень одного параметра й у площині двох параметрів.

            Для побудови таких областей необхідно у просторі їхніх значень нанести лінії, що відповідають межі стійкості. Тоді область, обмежена цими лініями буде являти  собою область стійкості.

            При побудові областей стійкості можна використати будь-які критерії стійкості, як аналітичні, так і графоаналітичні.

            У більше широкому плані поставлене завдання можна розглядати як окремий випадок виділення областей значень параметрів системи, які забезпечують однаковий розподіл коренів характеристичного рівняння в комплексній площині.

            Області значень параметрів системи з однаковою кількістю коренів характеристичного рівняння в правій  півплощині комплексної площини розподілу коренів називається D-областями, а сама розбивка простору значень параметрів називається D-розбиттям.

            Якщо в правій півплощині комплексної площини розподілу коренів є l-корінь, то область значень для такого розподілу корінь позначається D(n-l), де n-порядок характеристичного рівняння,  отже, загальна кількість коренів. Якщо всі n коренів перебувають у лівій півплощині (система стійка), то відповідна область значень параметрів системи для цього розподілу позначається відповідно D(n)і є областю стійкості. Загальна кількість D-областей   n + 1: (D(n), D(n – 1),…....D (0)).

            Для побудови D-областей, як вказувалося вище, можна користуватися будь-якими критеріями стійкості, але найбільш універсальним є приватний метод, запропонований. Соколовим О. О в 1940 р., який надалі був розвинутий в роботах Неймарка Ю. І.