Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 21

Якщо в процесі D- розбивки в характеристичному рівнянні замкнутої системи замінити оператор Лапласа р на jω, і прирівняти до нуля речовинну й мниму частини, що містять обоє конструктивних параметра  й , одержимо рівняння координат основної кривої D-розбивки, що є границею стійкості й відображенням мнимої осі комплексної площини розподілу корінь характеристичного рівняння на площині предметів  й .

Якщо ж у характеристичному рівнянні  замінити оператор р не величиною  jw, а р=-h+jw, де h-задана ступінь стійкості, а потім повторити побудова основної кривої D-розбивки, то отримана крива відобразить на площині параметрів   і   не мниму вісь, а вертикальну пряму, паралельну їй і зрушену від її вліво на відстань  h. Ця крива обмежує область, у якій ступінь стійкості вище заданої.

Якщо комплексних корінь характеристичного рівняння в загальному виді записати

те, беручи до уваги, що м= одержуємо L₁= Отже, якщо в характеристичне рівняння замкнутої системи замість р підставити не  (-h+jw), а (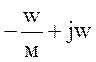 )= 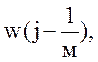виконати необхідні операції по визначенню рівняння основної кривої D-розбивки, те отримана в такий спосіб крива на площині конструктивних параметрів  і   відобразить два промені проведені на площині розподіли корінь й обмежить область із заданим ступенем колебательности м.

Розглянуті криві D-розбивки на площині параметрів  і   зображені на малюнку.

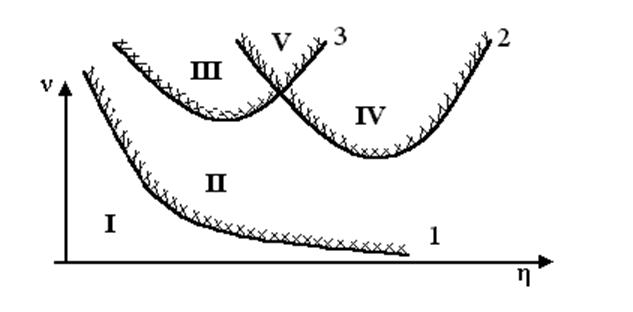На малюнку:

 крива 1 - границя стійкості (р=jw);

 крива 2 - границя заданого ступеня стійкості p = -h+j?);

крива 3 – границя заданого ступеня колебательности  ).

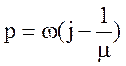Отримані криві розбивають простір можливих значень конструктивних параметрів САУ на 5 областей:

1. - область нестійкості, характеристичне рівняння замкнутої системи має корінь розташовані праворуч від мнимої осі в комплексній площині розподілу корінь.

2. - область стійкості, але зі ступенем стійкості менше заданої, і ступенем колебательности більше заданої, і ступенем колебательности більше заданої. Корінь характеристичного рівняння розташовані у відповідній області 2 комплексної й площини корінь.

3. - область стійкості зі ступенем стійкості менше заданої, і ступенем колебательности менше заданої. Корінь характеристичного рівняння перебувають в області 3 площини корінь.

4. - область зі ступенем стійкості більше заданої, і ступенем колебательности теж більше необхідної. Корінь на площині корінь у відповідній області 4.

5. - область у якій повністю виконуються вимоги в плані забезпечення необхідного ступеня стійкості й ступені колебательности. Характеристичне рівняння системи має всіх корінь, розташовані в області 5 площини корінь.

Зв'язок між кореневими оцінками й прямими показниками якості керування

Як указувалося вище, кореневі оцінки не є всебічними оцінками, вони характеризують як тільки певні сторони якості керування.

Так, ступінь стійкості h визначає швидкість загасання процесу, тобто час керування ty. Визначимо залежність ty від h.

Якщо найближчий корінь речовинний р_i=-h, то відповідному цьому кореню складова перехідного процеса

Будемо вважати, що наприкінці перехідного процесу  (5% первісного значення С_h). Отже наприкінці перехідного процесу через час t=ty маємо:

 звідки 

Логарифмуючи ліву й праву частини, одержуємо

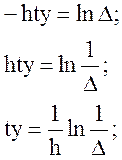
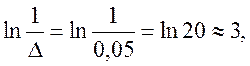
т. е.                                                                 

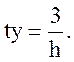
Якщо найближчих корінь комплексні сполучені  відповідним цим корінням складова перехідного процесу

Поклавши  наприкінці перехідного процесу при t= ty, одержимо трансцендентне рівняння

Визначаючи верхню границю перехідного процесу при  одержимо, як і раніше 

Отже, і в цьому випадку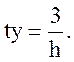             

Іншими словами абсолютно неважливо, які по характері корінь, речовинн або комплексні, визначають ступінь стійкості h. В обох випадках час керування ty визначаються однієї й тією же залежністю від h.

Варто нагадати, що перехідний процес має коливальну складову лише при наявності хоча б однієї пари комплексних сполучених корінь.

Припустимо, що є пара комплексних корінь.

  де μ = .

Відповідній цій парі корінь складова перехідного процесу

Визначимо зв'язок ступеня колебательности μ с загасанням амплітуди коливань  за один період, тобто зі ступенем загасання .

Предположим, що коливальна складова перехідного процесу системи, що відповідає зазначеній парі комплексних корінь має вигляд:

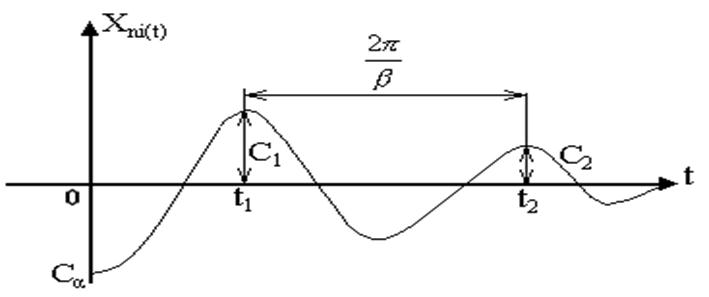У момент t, амплітудне значення 

Перехід колива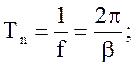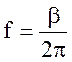нь        де Т_n -період коливань, з;  f – циклічна частота, Гц;  β - мнима частина комплексних корінь (кругова частота коливань).

Через період, тобто в момент t₂, амплітудне значення

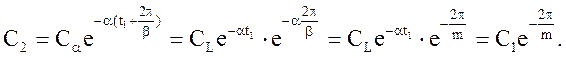
Загасання (ступінь загасання) за один період  

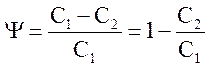
Підставляючи значення З₂, одержимо :

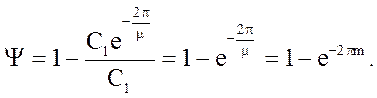
де m - кореневий показник колебательности

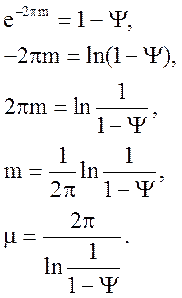
Звичайно, у САУ допускається загасання за період  не менш, ніж 90-98%, що відповідає діапазону μ від 2,72 до 1,57, а m від 0,37 до 0,64.

На закінчення необхідно підкреслити, що ступінь стійкості h визначає однозначно час керування ty, а ступінь колебательности ? і кореневий показник колебательности m - загасання коливань.

Діаграма Вишеградського

Використання діаграми Вышнеградского для оцінки якості процесу керування дозволяє графічно наближено визначити ступінь стійкості h і ступінь колебательности μ для систем третього порядку.

Порядок побудови діаграми полягає в наступному.

Нехай характеристичне рівняння замкнутої системи 3 ^го порядки має вигляд:

Приведемо його до нормованого виду, розділивши всі члени на

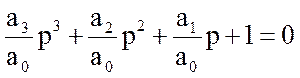
Позначимо:

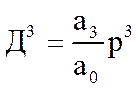,  тобто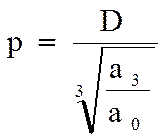

Після указаной підстановки одержимо:

де

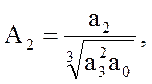
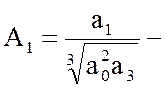            безрозмірні коефициенты.

Відповідно до критерію стійкості Вышнеградского границя стійкості визначається з рівняння    (А₁>0; А₂>0). У площині коефіцієнтів А₁,А₂ це рівняння відображається у вигляді гіперболи, асимптотами якої є осі координат, простір расположеное вище гіперболи є областю стійкості.