Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 13

an-1	an-3	an-5	an-7	……
an	an-2	an-4	an-6	……
0	an-1	an-3	an-5	……
0	an	an-2	an-4	……
0	0	an-1	an-3	……
0	0	an	an-2	……

Система автоматичного керування буде стійкою, якщо при виконанні необхідної умови стійкості (a_і>0), головний визначник матриці Гурвіца і всі його діагональні мінори додатні.

Критерій стійкості Вишнєградського.

Використовується тільки для систем 3 – го порядку, характеристичне рівняння якої має вигляд:

a₃p³₊ a₂p²+ a₁p+a₀=0.

Для стійкості систем 3 -  го порядку необхідно і достатньо, щоби при додатності всіх коефіцієнтів характеристичного рівняння добуток середніх коефіцієнтів був більше добутку крайніх, тобто: a₃>0; a₂>0; a₁>0; a₀>0; a₁∙ a₂> a₀ ∙a₃.

Цей критерій є частковим випадком критерію стійкості Гурвіца, тому як визначник матриці Гурвіца має вигляд

            ,

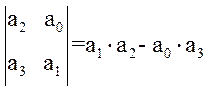то для стійкості системи потрібно щоби виконувалася вимога його додатності:

>0,

або:

,

що повністю співпадає з формулюванням критерію стійкості Вишнєградського.

Графічні критерії стійкості.

Критерій стійкості Михайлова.

З метою обґрунтування критерію, який був сформульований у 1936 році, розглянемо характеристичний поліном замкненої системи n – го порядку:

N(p) = a_npⁿ₊ a_n-1p^n-1+………….+a₀.

Підставимо в цей поліном p = jω.

N(jω) = a_n (jω) ⁿ₊ a_n-1 (jω) ^n-1+………….+a₀.

Виділимо в ньому дійсну та уявну частини:

N(jω) = X(ω) +jY(ω) = |N(ω)|∙e^jψ(ω),

де дійсна частина X(ω) = a₀- a₂ ω²+ a₂ ω²+ a₄ ω⁴- a₆ ω⁶…,

    а уявна частина Y(ω) = a₁ω - a₃ ω³+ a₅ ω⁵- a₇ ω⁷+…,

    модуль поліному |N(ω)| = ,

    аргумент поліному φ(ω) = arctg.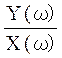

 Змінюючи параметр ω від 0 до ∞, побудуємо у комплексній площині множину векторів N(jω) і, поєднавши між собою їх кінці, отримаємо так званий годограф Михайлова.

Сформулюємо теорему: характеристичне рівняння не буде мати коренів у правій півплощині комплексної площини розміщення коренів характеристичного рівняння, якщо повний приріст аргументу ψ характеристичного поліному N(jω) при зміні ω від 0 до ∞, буде дорівнювати n∙π/2, де n – степінь полінома.

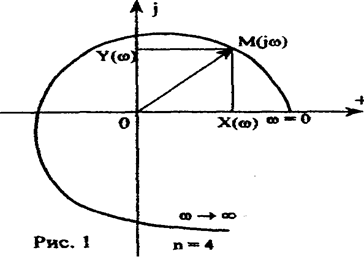Запишемо характеристичний поліном N(jω) у вигляді:

N(jω) = a_n(jω – p₁) (jω – p₂) (jω – p₃) ∙∙∙(jω – p_n),

де р_і – корені характеристичного рівняння.

Кожен співмножник, що позначений у дужках, являє собою комплексне число. При перемноженні комплексних чисел їх модулі перемножуються, а аргументи додаються. Тому загальний кут повороту Δφ_N(ω)  вектора N(jω) при зміні ω від 0 до ∞, дорівнюватиме сумі кутів повороту окремих співмножників Δφ_і(ω), що записані у дужках, тобто:

Δφ_N (ω)   = Δφ₁(ω) + Δφ₂(ω) + Δφ₃(ω) + Δφ₄(ω) + ∙ ∙ ∙ + Δφ_n(ω).

Визначимо кути повороту окремих співмножників в залежності від типу коренів.

Нехай корінь р₁ є дійсне від’ємне число, р₁ = -α₁ (α₁>0). Перший співмножник характеристичного поліному N(jω)  матиме вигляд (jω + α₁), тобто це є комплексне число з модулем |jω + α₁)| =  та аргументом φ₁(ω) = arctg. При зміні ω від 0 до ∞ аргумент φ₁(ω) зміниться від 0 до π/2, тобто приріст аргументу даного співмножника Δφ₁(ω) = π/2- 0 = π/2.

Якщо припустити, що всі інші корені характеристичного рівняння теж є дійсними від’ємними числами, то загальний кут повороту вектора N(jω) дорівнюватиме Δφ_м(ω) = n∙π/2.

Припустимо, що корінь р₂ є дійсне додатне число, р₂ = α₂. Другий співмножник характеристичного поліному N(jω)  матиме вигляд (jω – α₂), тобто це є комплексне число з модулем |jω – α₂)| =  та аргументом φ₂(ω) = -arctg. У такому випадку при зміні ω від 0 до ∞ аргумент φ₁(ω) зміниться від 0 до (-π/2), тобто приріст аргументу даного співмножника Δφ₁(ω) = (-π/2)- 0 = - π/2.

З отриманого можна зробити висновок, що кожний дійсний від’ємний корінь збільшує загальний кут повороту вектора М(jω)  на π/2, а кожний додатний корінь зменшує його на π/2.

Розглянемо вплив комплексних спряжених коренів з від’ємною та додатною дійсними частинами. Нехай 3-й та 4-й корені є комплексними спряженими з від’ємною дійсною частиною: р_3,4 = -α₃jβ₃, тому відповідні співмножники характеристичного поліному N(jω)  матимуть вигляд (jω +α₃-jβ₃)∙(jω + α₃+jβ₃). Модулі кожного з співмножників дорівнюють |(jω +α₃-jβ₃)|= =, а |(jω + α₃+jβ₃)| =. Аргументи відповідно: φ₃(ω) = arctg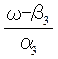,      φ₄(ω) = arctg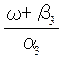. При зміні ω від 0 до ∞ аргумент φ₃(ω) зміниться від γ₃ = arctg 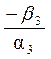 до π/2, φ₄(ω) від γ₄ = arctg  до π/2, тобто загальний приріст аргументів обох векторів Δφ_3,4(ω) = Δφ₃(ω) + Δφ₄(ω) =      = (π/2 - γ₃ )+ (π/2 - γ₄) = π/2 + arctg  + π/2 - arctg  = 2∙ π/2. Іншими словами, кожний з двох спряжених комплексних коренів з від’ємною дійсною частиною, як і один дійсний від’ємний корінь, збільшує загальний кут повороту вектора N(jω)  на π/2. Неважко показати, що кожний з двох спряжених комплексних коренів з додатною дійсною частиною, наприклад для   р_5,6 = α₅jβ₅, як і один дійсний додатний корінь, зменшує загальний кут повороту вектора N(jω)  на π/2, тобто  Δφ_5,6(ω) = - 2∙ π/2. Таким чином, наявність коренів з від’ємною дійсною частиною приводить до збільшення аргументу комплексного поліному N(jω) на величину π/2, а з додатною дійсною частиною до зменшення на ту ж величину π/2.

Нехай кількість коренів характеристичного рівняння у правій на півплощині дорівнює l; завдяки їм, зміна аргументу дорівнюватиме -l∙π/2, решта (n-l) коренів, що знаходяться у лівій півплощині, змінять аргумент на величину (n-l)∙π/2.

Сумарний приріст кута:

Δφ_м(ω) = (n-l)∙π/2 + (-l∙π/2) = n∙ π/2 - l∙π,

Тобто якщо l = 0, то Δφ_м(ω) = n∙ π/2, що і потрібно було доказати.

Для стійкості системи автоматичного керування необхідно і достатньо, щоби вектор комплексного поліному N(jω), кінець якого при зміні ω від 0 до ∞ описує криву(годограф)  Михайлова, мав кут повороту n∙ π/2.