Більш поширене інше формулювання критерію Михайлова: Для стійкості системи автоматичного керування необхідно і достатньо, щоби при зміні ω від 0 до ∞ годограф Михайлова пройшов послідовно у додатному напрямку n квадрантів.
При тому слід пам’ятати, що взагалі ω являє собою деякий штучний параметр, який за своєю фізичною суттю не є частотою.
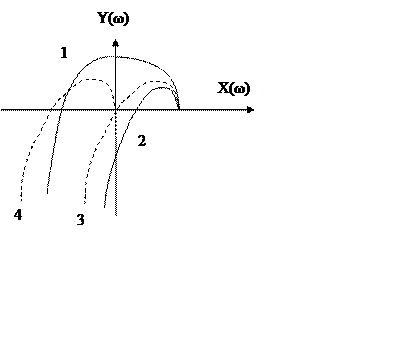
На рисунку зображені криві Михайлова для різних за стійкістю систем керування 3 –го порядку. Як видно з рисунка, у відповідності до критерію стійкості Михайлова годограф 1 відповідає стійкій системі, 2 – нестійкій, а 3 та 4 – системам, які знаходяться на межі стійкості. Причому, значення ω, при якому годограф 3 проходить через початок координат, відповідає саме частоті незатухаючих коливань, характеристичне рівняння у даному випадку має принаймні одну пару чисто уявних кореня з нульовою дійсною частиною.
 |
Критерій стійкості Найквіста.
На відміну від попередніх випадків, критерій стійкості Найквіста дозволяє робити висновки щодо стійкості замкнених систем по вигляду АФЧХ розімкненої системи.
Будемо вважати, що функція передачі розімкненої системи має вигляд:
,
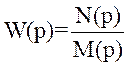де N(p),M(p) – відповідно чисельник та знаменник функції передачі. При тому слід пам’ятати, що в мінімально фазових системах порядок чисельника m не перевищує порядку знаменника n.
При підстановці р =jω в W(p) отримаємо комплексний коефіцієнт передачі
,
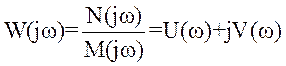де U(ω), V(ω) – дійсна та уявна частини комплексного коефіцієнту передачі.
Якщо змінювати ω в межах -∞<ω<+∞, то отримаємо повну АФЧХ як дзеркальне відображення характеристик отриманих при зміні ∞ в межах -∞<ω<0 та 0<ω<+∞. Оскільки m≤n, то при частоті ∞→0 модуль W(jω) , буде наближатися до нуля, тобто АФЧХ розімкненої системи має закінчуватися в початку системи координат.
Сформулюємо вимоги до амплітудно-фазової частотної характеристики розімкненої системи, при виконанні яких cсистема автоматичного керування в замкненому стані буде стійкою.
Спочатку розглянемо стійкі статичні розімкнені системи, тобто такі, у яких корені характеристичного рівняння знаходяться у лівій півплощині.
Знаменник функції передачі замкненої системи керування F(р):
F(р)=1+W(p)=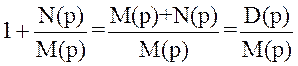
,
де М(р) – характеристичний поліном розімкненої системи,
D(p) – характеристичний поліном замкненої системи.
Зробимо заміну р=jω:
F(jω)=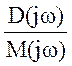
.
Варіюючи ω від -∞ до +∞, визначимо приріст аргументу
ΔφF(ω)= φD(ω)-φM(ω).
Якщо всі корені характеристичного рівняння замкненої системи n – го порядку М(р)=0 знаходяться у лівій півплощині (система стійка), то, у відповідності до критерію стійкості Михайлова, загальний приріст аргументу характеристичного полінома замкненої системи φD(ω) повинен складати n∙π/2, тобто:
φD(ω)= n∙π/2.
Оскільки, як було умовлено, розглядаються стійкі системи у розімкненому стані, то загальний приріст аргументу характеристичного полінома розімкненої системи φM(ω) теж повинен складати n∙π/2, тобто:
ΦM(ω)= n∙π/2.
Таким чином, загальний приріст аргументу комплексного полінома F(jω):
ΔφF(ω)= n∙π/2- n∙π/2=0.
Це означає, що годограф F(jω) не повинен охоплювати початок координат.
АФЧХ W(jω) відрізняється від полінома F(jω) на 1. Тому краще користатися годографом амплітудно-фазової частотної характеристики розімкненої системи W(jω).
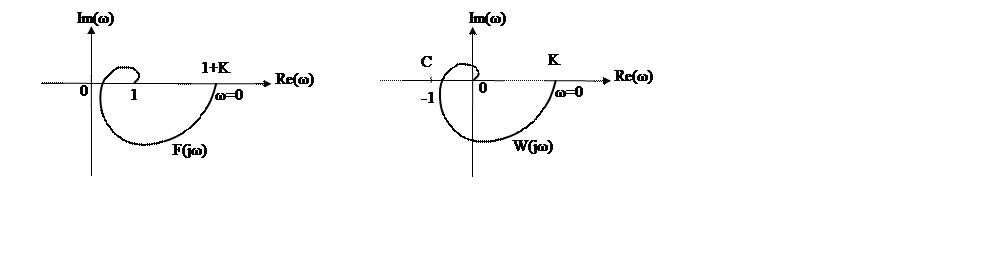
Розглянемо відображення на комплексній площині годографів F(jω) і W(jω). Як видно з рисунка, обидві криві ідентичні, якщо не враховувати зсув однієї з них по відношенню до початку координат на одиницю. На рисунках показано, що при ω=0 початкове значення обох кривих теж відрізняються на 1, при тому зрозуміло, що літерою К позначений коефіцієнт передачі розімкненої системи.
З рисунка випливає,
що для того , щоби стійка система у розімкненому стані була стійкою у
замкненому стані, необхідно і достатньо аби АФЧХ розімкненої системи W(jω) не охоплювала критичну точку С з координатами 
.
Якщо W(jω) проходить через точку
С, замкнена система буде знаходитися на межі стійкості, це відповідає
встановленню незатухаючих коливань. Цей факт випливає з того, що при перетині
АФЧХ W(jω) точки С виконується рівняння:
W(jω) = -1+j0,
тому
1 + W(jω) = 0.
Тобто комплексний характеристичний поліном замкненої системи F(jω)=1+ W(jω) дорівнює нулю. Якщо цей поліном можна записати у вигляді:
F(jω)=an(jω-p1)( jω-p2)…..( jω-pn),
тому рівність нулю полінома можливе лише при наявності хоча б одного уявного кореня рі з нульовою дійсною частиною, тобто рі= jω, а це означає знаходження замкненої системи на межі стійкості.
Якщо розімкнена система знаходиться на межі стійкості, вимоги до АФЧХ розімкненої системи для забезпечення стійкості замкненої системи не змінюються, лише змінюється вигляд АФЧХ.
Визначимо вимоги до АФЧХ W(jω), якщо розімкнена система нестійка і l коренів характеристичного рівняння знаходяться у правій півплощині.
Пам’ятаючи про те, l коренів, що розташовані у правій півплощині, при зміні ω від -∞ до ∞ дають приріст аргументу характеристичного полінома (- l∙π), а (n-l) коренів характеристичного рівняння, що знаходиться у лівій півплощині – (+n∙π), тому загальний приріст буде:
ΔφF(ω)= φD(ω)-φM(ω)=n∙π-(( n-l) π-l∙π)=l∙2π.
Це означає, що для того, щоби нестійка у розімкненому стані система автоматичного керування була стійкою у замкненому стані, необхідно і достатньо аби крива F(jω) охоплювала початок координат у додатному напрямку l раз. По відношенню до АФЧХ розімкненої системи критерій Найквіста у такому випадку можна сформулювати таким чином:
Для того, щоби
нестійка у розімкненому стані система автоматичного керування була стійкою у
замкненому стані, необхідно і достатньо аби крива АФЧХ розімкненої системи W(jω) охоплювала критичну точку С з координатами l разів за напрямком годинникової
стрілки.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.