Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 3

Графік залежності керованої величини h  від зовнішнього впливу Q_в в астатичних системах має вигляд:

 Астатичні системи мають високу статичну точність керування, але, при цьому, в таких системах у порівнянні зі статичними підвищується час перехідного процесу, коливальність процесу керування, мають місце значні динамічні відхилення керованої величини від сталого значення.

По наявності додаткового джерела енергії розрізняють системи керування прямої й непрямої дії. Так, у розглянутій статичній системі робота по переміщенню регулювального органа здійснюється за рахунок сили, що виштовхує поплавок, тобто за рахунок енергії об'єкта. Таку систему керування варто віднести до систем прямої дії. В астатичній системі регулювальний орган переміщується за допомогою двигуна Д, якому для його роботи, як і для вимірювальної схеми та підсилювачу П, необхідні додаткові незалежні джерела енергії. У цьому випадку маємо систему керування непрямої дії.

По наявності в системі елементів, що перетворюють безперервну інформацію в дискретну форму, системи керування діляться на безперервні та дискретні системи. Дискретні системи містять хоча б один елемент, вихідна величина якого приймає дискретні значення при плавній зміні вхідної величини. Існують різні способи дискретизації безперервної інформації за допомогою різних релейних елементів (квантування за рівнем), імпульсних елементів (квантування за часом), кодоімпульсних модуляторів (квантування за рівнем і за часом). При цьому функціональна схема повинна містити специфічні елементи, що дозволяють перетворювати характер інформації й обробляти перетворену інформацію по певному алгоритму. Наприклад:

На функціональній схемі прийняті позначення:

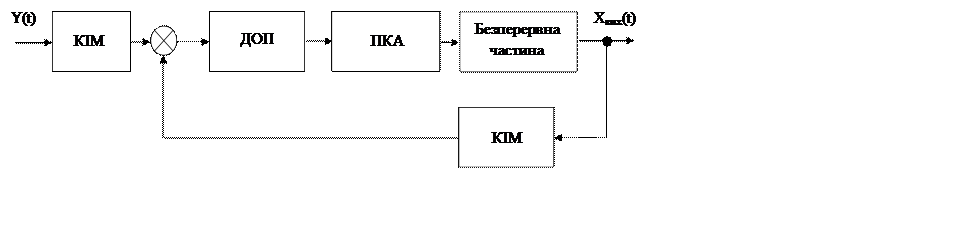КІМ - кодоімпульсний модулятор;

ДОП - дискретний обчислювальний пристрій;

ПКА - перетворювач код-аналог;

Y(t) - завдання;

X_вих(t) - керована величина.

Якщо безперервна величина представлена у вигляді якого-небудь цифрового коду, то такі дискретні системи прийнята називати цифровими, у структурі цих систем звичайно є аналого-цифрові (АЦП) і цифро-аналогові (ЦАП) перетворювачі й цифровий обчислювальний пристрій (ЦОП).

По наявності нелінійних елементів системи діляться на лінійні й нелінійні системи. При цьому якщо в системі є хоча б один нелінійний елемент, то така система називається нелінійною. До нелінійних елементів відносять елементи системи, у яких у сталому режимі вихідна величина не прямо пропорційна вхідній величині.

По наявності місцевих зворотних зв'язків розрізняють одноконтурні й багатоконтурні системи керування.

Залежно від числа керованих величин системи бувають одномірні й багатомірні. При цьому багатомірні системи можуть бути системами зв'язаного й незв'язаного керування.

По функціональному  призначенню системи класифікуються як системи автоматичного керування температурою, тиском, вологістю і т.і.

По виду енергії, яка використовується для керування, розрізняють електричні, пневматичні, гідравлічні, механічні й т.д. системи керування.

Математичне моделювання лінійних систем керування.

Лінеаризація нелінійних диференціальних рівнянь динаміки САУ.

Математичний опис, необхідний для дослідження процесів керування, виконується у вигляді диференціальних, інтегральних або алгебраїчних рівнянь.

Динамічні процеси в інерційних системах й їхніх елементах описуються диференціальними або інтегральними рівняннями, що називають рівняннями динаміки, оскільки відбивають зміна в часі зміна координат стану елементів з урахуванням швидкості, прискорення й т.д. (1-я, 2-я … похідні).

Безінерційні елементи, як у перехідному, так й у сталому режимі, описуються алгебраїчними рівняннями, називаними рівняннями статики, оскільки відбивають стале співвідношення вхідних і вихідних величин.

Якщо параметри елементів зосереджені (у цьому випадку координати стани є як тільки функціями часу), то рівняння динаміки є звичайним диференціальним рівнянням. Системи з розподіленими параметрами описуються рівняннями в частинних похідних.

У загальному випадку диференціальні рівняння нелінійні, але при малих відхиленнях координат системи від стану рівноваги нелінійні рівняння можна приблизно замінити лінійними. Ця процедура заміни нелінійного рівняння лінійним називається лінеаризацією.  Чим менше відхилення координат від стану рівноваги, тим точніше лінеаризоване рівняння описує реальний процес.

При складанні математичного опису будь-якої складної системи її попередньо представляють у вигляді сукупності окремих елементів взаємозалежних між собою, установлюють фізичний зміст вхідних і вихідних величин.

Розглянемо якийсь елемент системи автоматичного керування, на  який впливають одночасно дві вхідних величини (х₁(t); х₂(t)), в результаті чого змінюється вихідна величина х₃(t).

 

Припустимо, що для розглянутого елемента складене диференціальне рівняння, що виявилося нелінійним.

.

Крапки над позначенням вхідних і вихідних  змінних означають похідну, а їхня кількість - порядок похідній.

 З огляду на складності аналізу нелінійних рівнянь, а також той факт, що в процесі керування всі вхідні й вихідні координати мало відхиляються від деяких сталих значень, лінеаризація представляється доцільної.

Допустимо, що сталий процес у системі має місце при деяких постійних значеннях  х₁₀, х₂₀, х₃₀, тобто х₁(t)|₀=x₁₀; х₂(t)|₀=x₂₀; х₃(t)|₀=x₃₀, а .

Тоді, з огляду на те, що в сталому режимі всі похідні змінних дорівнюють нулю, рівняння приймає вид:

.

Позначимо значення змінних у динаміку:

х₁(t) = х₁₀ + Δх₁(t);  = 0+Δ;

х₂(t)  = х₂₀ + Δх₂(t); = 0+Δ;   = 0+Δ;

х₃(t)  = х₃₀ + Δх₃(t);  = 0+Δ;      = 0+Δ;    = 0+Δ.

Розкладемо нелінійну функцію  у кратний ряд Тейлора:

,

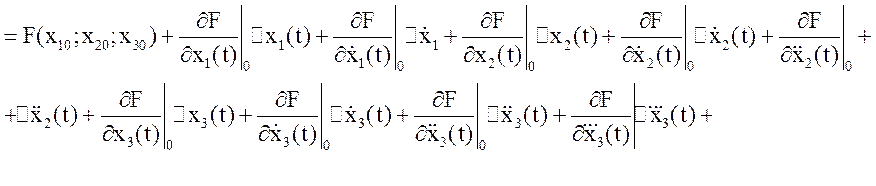
де Δх₁(t);  Δх₂(t);  Δх₃(t);   - приріст відповідних змінних;

У рівнянні прийняті  позначення виду 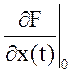, які варто розуміти як значення часткової похідної функції F по х при значеннях змінної х(t)|₀ у сталому режимі.

Віднімаючи рівняння сталого режиму і відкидаючи члени вищого порядку малості, одержимо: