З огляду на
перераховані положення відносно виду ВЧХ й її зв'язку з
перехідними характеристиками , неважко визначити
основні показники якості керування: час керування ty, перерегулювання σ,%, що
встановилася помилку керування ![]() .
.
Оцінка якості керування по АЧХ замкнутих систем
Як частотні оцінки можна використати різні значення частот, що визначають вид АЧХ замкнутої системи.
Розглянемо АЧХ стійкої замкнутої коливальної системи
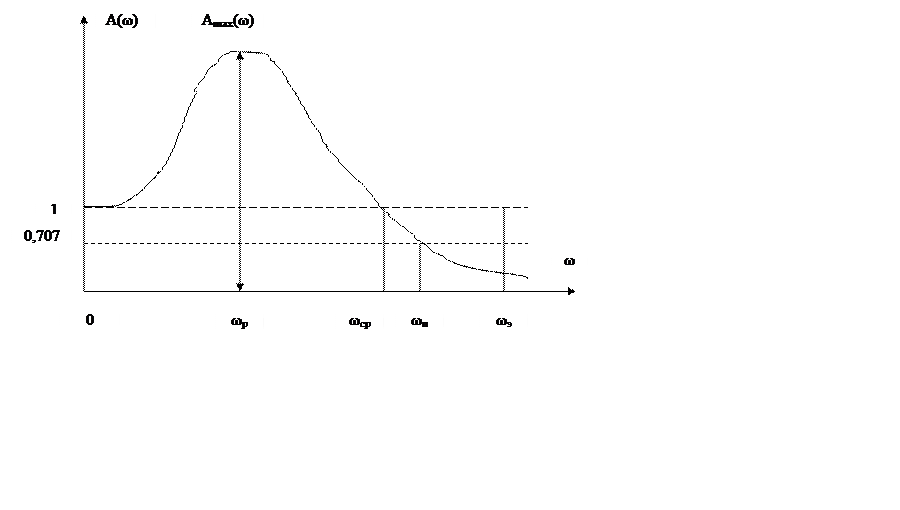
На графіку прийняті позначення:
ωp- резонансна частота, що відповідає піку АЧХ;
ωср- частота зрізу відповідній умові А(ωcр)=1;
ωп-частота, що відповідає верхній границі смуги пропущення, обумовлена з умови А(ωп)=0,707;
ωэ-эквивалентная
частота смуги пропущення, обумовлена по вираженню
ωэ =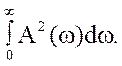
Еквівалентна частота смуги пропущення являє собою підставу прямокутника, висота якого дорівнює одиниці, а площа дорівнює площі під кривою квадрата А(?).
Оскільки резонансна частота замкнутої системи ωp у багатьох випадках близька до частоти зрізу розімкнутої системи ωcp і відповідає частоті коливань у замкнутій системі, час досягнення першого максимуму на перехідній характеристиці може бути визначене по наближеній залежності
tм 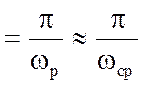
Якщо перехідний процес у системі закінчується через 1-2 коливання, то час керування tу можна визначити
tу= (1÷2) 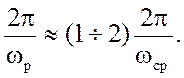
Необхідне значення ωp визначається по АЧХ замкнутої системи, а ωcp – по крапці перетинання окружності одиничного радіуса із центром на початку координат з АФЧХ розімкнутої системи.
Оцінки якості по АФЧХ розімкнутих систем.
При використанні
критерію стійкості Найквиста
запас стійкості можна визначити
по видаленню АФЧХ
розімкнутої системи від критичної крапки ІЗ![]() Із цією метою
вводяться поняття запасу стійкості по модулі
й запасу стійкості по фазі.
Із цією метою
вводяться поняття запасу стійкості по модулі
й запасу стійкості по фазі.
Запас стійкості по модулі
визначається відстанню від крапки перетинання АФЧХ
розімкнутої системи з речовинною віссю до крапки З![]()
Для випадку
умовної стійкості, зображеного
на малюнку, запас стійкості по модулі визначається
розташуванням крапок
а й d, величинами, вираженими
звичайно в децибелах 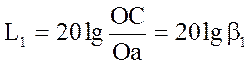 й
й 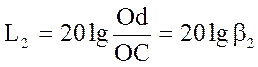 .
.
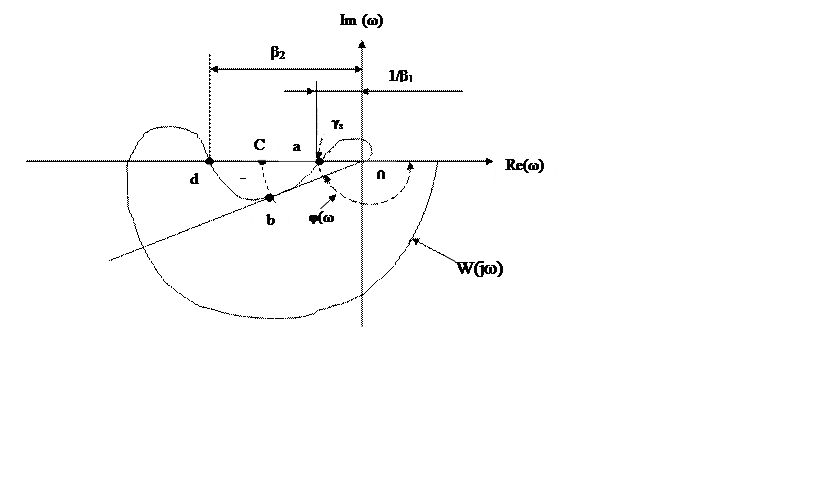
Запас стійкості по модулі тим більше, чим більше L1 й L2, у добре демпфированых системах ці величини становлять приблизно 6÷20dв, що відповідає 2?10 у лінійному масштабі.
У випадку
абсолютної стійкості зміст
має тільки величина ![]() тому
що
тому
що ![]() .
.
Фізичний зміст запасу стійкості по модулі полягає в тому, що він показує, у скільки разів можуть зміниться значення модуля АФЧХ (коефіцієнта передачі) розімкнутої системи до втрати стійкості.
впливи, Що Обурюють, що приводять до зміни модуля комплексного коефіцієнта передачі W(j? ) без зміни фазових зрушень, називаються збурюваннями по модулі.
Аналіз малюнка
показує, що розглянута система може втратити стійкість не тільки при зменшенні L1 й L2
(при переміщенні крапок a й d уздовж
осі абсцис убік крапки З![]() але й при повороті всіх
векторів W(jω) по годинній стрілці на кут γз (у крапку C
але й при повороті всіх
векторів W(jω) по годинній стрілці на кут γз (у крапку C![]() попадає крапка b).
попадає крапка b).
Запасом стійкості по
фазі називається кут ![]() з=180º+
з=180º+![]() (ω),
де
(ω),
де ![]() (ω) - аргумент комплексного
коефіцієнта передачі розімкнутої системи при частоті, для якої значення АЧХ дорівнює одиниці.
(ω) - аргумент комплексного
коефіцієнта передачі розімкнутої системи при частоті, для якої значення АЧХ дорівнює одиниці.
Запас стійкості по фазі визначає,
на який кут по годинній
стрілці можливий поворот векторів АФЧХ
розімкнутої системи до втрати стійкості. У
добре демпфированых системах запас стійкості по фазі становить
30º![]() ÷60?.
÷60?.
впливи, Що Обурюють, що змінюють зрушення по фазі без зміни модуля(j? ) називаються збурюваннями по фазі.
До збурювань по модулі варто віднести всі ті збурювання, які, у результаті їхньої дії, змінюють коефіцієнти передачі окремих елементів системи. Найпоширенішими збурюваннями по фазі є збурювання, що приводять до змін чистого запізнювання в системах керування.
Недоліком розглянутих оцінок є те, що для визначення запасу стійкості необхідно знаходити два числа: βз й γз. Ні те, ні інше окремо, ні обоє разом ніяк не визначають однозначно чисельно хоча б один з основних прямих показників якості керування. Щодо цього більш зручно оцінювати якість керування по частотному показнику колебательности.
Частотний показник колебательности
Розглянемо АФЧХ розімкнутої системи:
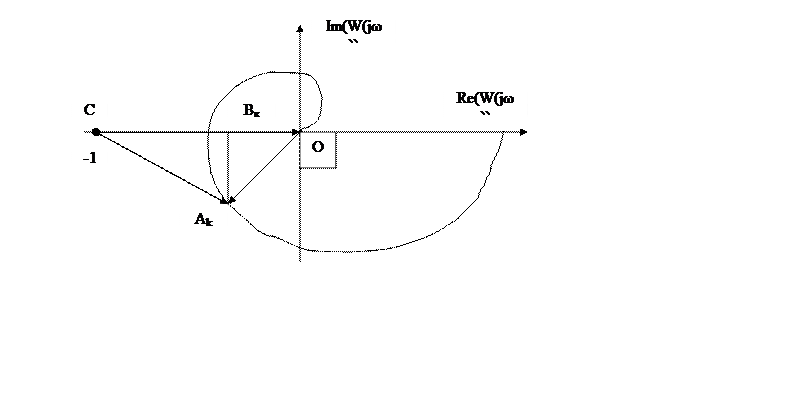
На малюнку ![]()
Розглянемо відносини: 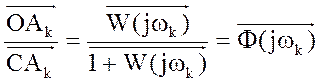 ,
де
,
де ![]() вектор АФЧХ
замкнутої системи. АЧХ замкнутої системи А(?)
являє собою модуль АФЧХ.
вектор АФЧХ
замкнутої системи. АЧХ замкнутої системи А(?)
являє собою модуль АФЧХ.
А(w)=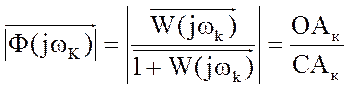
Відношення 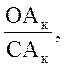 будучи
начением АЧХ
замкнутої системи, однозначно залежить від ступеня стійкості.
Чим ближче АФЧХ розімкнутої системи підходить до
крапці З, тим
менше відрізок Сак і більше відрізок ОАk,
а отже, тим більше максимум зазначеного відношення. Якщо АФЧХ
пройде через крапку
З, то довжина відрізка Сак стає рівної до нуля, а значення А(ω)- нескінченності. При
цих умовах система буде на границі стійкості, у ній виникнуть незатухаючі коливання.
будучи
начением АЧХ
замкнутої системи, однозначно залежить від ступеня стійкості.
Чим ближче АФЧХ розімкнутої системи підходить до
крапці З, тим
менше відрізок Сак і більше відрізок ОАk,
а отже, тим більше максимум зазначеного відношення. Якщо АФЧХ
пройде через крапку
З, то довжина відрізка Сак стає рівної до нуля, а значення А(ω)- нескінченності. При
цих умовах система буде на границі стійкості, у ній виникнуть незатухаючі коливання.
Із сказаного
випливає що максимум відносини А(ω)=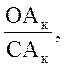 характеризує колебательность системи.
характеризує колебательность системи.
Частотним показником колебательности М називається максимальне значення АЧХ замкнутої системи при початковій ординаті, рівній одиниці, т.е являє собою відносну висоту резонансного піка.
Розглянемо більш докладно частотний показник колебательности як оцінку якості.
Для судження про частотний показник колебательности М замкнутої системи на комплексній площині W(j?) варто нанести лінію відповідному заданому значенню М=const.
Думаємо, що комплексний коефіцієнт передачі розімкнутої системи представлена у вигляді W(j?) = U(?)+j(?), де U(?) і V(?) - значення речовинної й мнимої частин відповідно.
Тоді з вищенаведеного малюнка випливає, що
ОАк=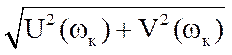
Сак=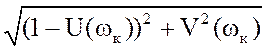
Отже:
М2=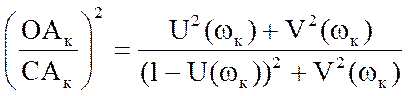
Або інакше:
М2(1-U(ωк)))2+М2V2(ωк) =U2(ωк) +V2(ωк)
Розрив дужки, одержимо
М2-2М2U(ωк) +M2U2(ωк) +M2V2(ωк) =U2(ωк) +V2(ωк);
(М2-1)U2(ωк) +(M2-1)V2(ωк) -2M2U(ωк) = - M2.
Розділивши почленно на М2-1:
U2(ωк)
+V2(ωк) 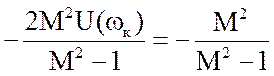

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.