Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 17

Повертаючись до розглянутого приклада, припустимо, що досліджується вплив на стійкість САУ коефіцієнта підсилення підсилювача К_у й постійної часу об'єкта Т_об.

Характеристичний поліном розглянутої САУ має вигляд:

F(p)=Т_имТ_обр³+(Тім+Т_об)р²+р+К_уК_имК_об=Т_об(Т_имр³+р²)+К_уК_имК_об+р+Т_имр².

У цьому виразі можна прийняти позначення:

μ=Т_об;        М(р) =Т_имр³+р²;

ν=К_у;      N(р) =К_имК_об;

                  Z(р) =р+Т_имр²,

де μ і ν - параметри, вплив яких на стійкість САУ досліджується;

 М(р) і N(p) - поліноми, що є співмножниками μ і ν відповідно;

Z(р) - поліном, що не містить ні μ, ні ν.

Здійснивши заміну р=jω, одержимо:

F(jω)= μ M(jω)+ ν N(jω)+Z(jω)=U(ω) +j(ω),

F (jω) є комплексним багаточленом, у дійсну U(ω) і уявну частину V(ω) якого лінійно входять параметри μ і ν.

У загальному вигляді дійсна й уявна частини можуть бути записані в такий спосіб:

U(ω)=μM₁(ω)+νN₁(ω)+Z₁(ω);

V(ω)=μM₂(ω)+νN₂(ω)+Z₂(ω);

Коливальній границі стійкості відповідає проходження годографа Михайлова через початок координат комплексної площини, тобто рівність нулю дійсної й уявної частин комплексного характеристичного полінома. Отже:

μM₁(ω)+νN₁(ω)+Z₁(ω)=0;

μM₂(ω)+νN₂(ω)+Z₂(ω)=0;

            Визначення параметрів μ і ν здійснюють шляхом рішення системи рівнянь:

μ = 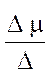;     ν = ,

де                                                   ;

;

.

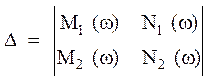
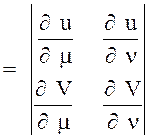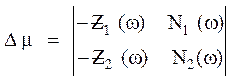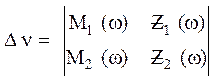            У нашому прикладі, після підстановки р =jω, характеристичної поліном, з урахуванням того, що Т_об=μ, а К_у=ν здобуває вид:

F(jω)=μ(-jТ_имω³–ω²⁾ +νК_имК_об+(jω-тімω²⁾ =μ(-ω²⁾ +νК_имК_об–Т_имω²+j(μ(Тімω²)+ω);

U(ω)=μ∙ (-ω²⁾ +ν∙ К_имК_об–Т_имω²=0;

V(ω)=μ∙ ω(-Тімω²⁾ +ν∙ 0+ω=0,

де можна позначити:

M₁(ω) = -ω²;              N₁(ω) = Кім К_об;       Z₁(ω) = -Тім ω²;

M₂ (ω) = -Тім ω³;       N₂ (ω) = 0;                 Z₂ (ω) = ω;

отже:

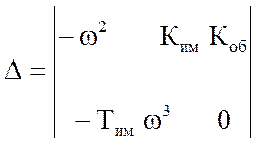= Кім К_об Тім ω³;

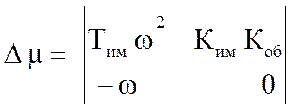= Кім К_об ω;

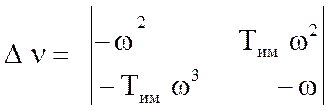=ω³+Тім²ω⁵=ω³(1+Тім² ω²⁾;

μ= = ;

ν =  = ;

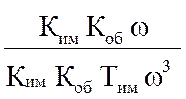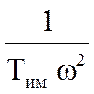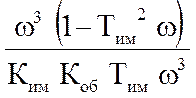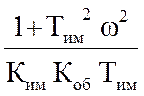 Змінюючи ω від - до + , можна розрахувати й  побудувати в  площині параметрів  μ, ν основну криву D- розбивки, що є коливальною границею стійкості.

Основна крива доповнюється двома особливими прямими, рівняння яких виходять у результаті дорівнюючи до нуля коефіцієнтів при нульовій і старшій похідній характеристичного полінома,т.е:

       Кім К_об · К_у= 0,

Тім Т_об = 0,

звідки:

К_у = ν = 0,

   Т_об = μ  = 0.

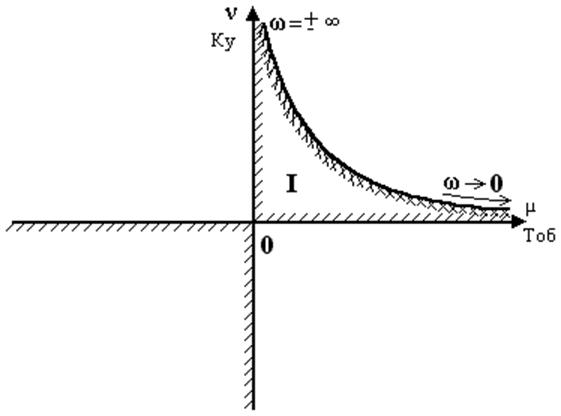
На малюнку представлена основна крива D-розбивки й дві особливі прямі співпадаючі з осями координат. Основна крива штрихується подвійним штрихуванням, оскільки обходиться двічі, будучи парною функцією ?.

Правила штрихування:

Спочатку штрихується основна крива D-розбивки, а потім особливі прямі.

Основна крива штрихується ліворуч при збільшенні ω від - до + , якщо > 0;           а  праворуч, якщо < 0. Оскільки при ω = 0 визначник  міняє свій знак на протилежний, те основна крива обходиться двічі, отже двічі заштриховується;

Особливі прямі до крапки перетинання з основної кривої штрихуються одиночним штрихуванням таким чином, щоб їхні штрихування й штрихування основній кривій були спрямовані друг до друга або в різні сторони.

У розглянутому прикладі крива D-розбивки дозволяє відразу визначити область стійкості. Область, обмежена заштрихованими усередину лініями (область I) є областю стійкості, і це твердження не вимагає додаткової перевірки.  Визначення зазначеної області здійснювалося, виходячи з первісного положення про те, що основна крива D-розбивки є границею коливальної стійкості й саме тому, відповідно до критерію стійкості Михайлова, речовинна й мнима частини характеристичного полінома прирівнювалися до нуля.

D-розбивка по двох конструктивних параметрах можна здійснити, використовуючи які-небудь інші критерії стійкості. Розглянемо можливість застосування критерію Гурвица.

У характеристичному рівнянні розглянутої як приклад системи

Т_имТ_обр³+(Тім+Т_об)р²+р+К_обК_имК_у=0

варьируемыми параметрами є =Т_об; =К_у, інші параметри фіксовані.

Система 3-го порядку, відповідно до  критерію Вышнеградского, перебуває на границі стійкості при рівності добутків середніх і крайніх коефіцієнтів характеристичного рівняння, тобто:

(Тім+Т_об)1=К_обК_имК_уТ_имТ_об ,

звідки:

К_у= =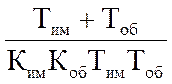

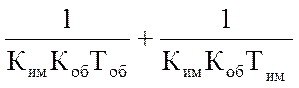
Графік залежності К_у=f(Т_об), що представляє собою геометричну суму гіперболи й прямої лінії, паралельної осі абсцис, є основної кривої D-розбивки.

Рівняння особливих прямих, як і вказувалося вище, перебувають із умови рівності нулю коефіцієнтів при старшій і нульовій похідній характеристичного рівняння. У цьому випадку, рівняння особливих прямих перебувають із умов:

Т_имТ_об=0;

     К_уК_имК_об=0,

звідки:

Т_об = μ  = 0,

К_у = ν = 0.

Ці прямі збігаються з віссю ординат і віссю абсцис відповідно.

Для системи 3-го порядку такий підхід набагато простіше, ніж розглянутий вище, але при цьому виникають певні утруднення у виділенні області стійкості шляхом штрихування основної кривої D-розбивки й особливих прямих.

Якість керування.

Стійкість САУ характеризує можливість виконання поставленой перед системою завдання керування в принципі, але не дає відповіді на питання про якість її виконання. Стійкі САУ працездатні, але проте необхідно, щоб процес керування здійснювався при забезпеченні певних якісних показників.

У стійких САУ перехід від одного сталого стану до іншого сталого стану, залежно від значень конструктивних параметрів системи може происходств за різний інтервал часу. Характеризуватися різними динамічними й статичними (сталими) помилками, здійснюватися монотонно або з  певною кількістю коливань щодо нового сталого стану.

Зазначені властивості, як і деякі інші, у цілому визначають якість процеса керування. При всьому їхньому різноманітті можна виділити трохи найбільш істотних, які з найбільшою повнотою визначають якість керування майже для всіх САУ.