Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 20

У реальних САУ вплив, що задає, в, як правило, відмінно від нуля, отже, і . Тому всі основні показники якості керування можуть бути визначені по основних формулах, наведеним на початку роздягнула.

Как показано вище, у статичних системах, що стежать, стала помилка в абсолютних одиницях виміру

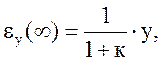
а в статичних стабілізуючих системах

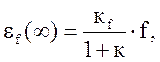
де в и f – вхідні впливи у відповідних режимах.

Коефіцієнти, що коштують при вхідних змінних у и f  у правій частині зазначених виражень, що визначають тангенс кута нахилу статичних характеристик  і  прийнято називати коефіцієнтом статизма або просто статизмом.

Відносна величина сталої помилки 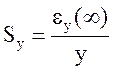  або 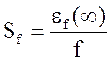  називається коефіцієнтом статизма системи по відповідному каналі.

При цьому коефіцієнті статизма системи щодо впливу, що задає, визначається вираженням:

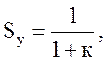
який чисельно дорівнює сталій помилці у відносних одиницях виміру (частках).

Той же коефіцієнт щодо впливу, що обурює

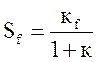
Непрямі оцінки якості керування

Прямі показники якості керування, як указувалося вище, визначаються безпосередньо по графіках перехідних характеристик. Природно, що для побудови цих графіків необхідно або вирішити відповідні диференціальні рівняння динаміки, або побудувати їх за результатами проведення натурного експерименту. І перше, і друге виконати часто буває досить важко, а іноді й неможливим у силу відсутності необхідних апаратур або за умовами технології, що регламентує проведення необхідних експериментів.

У зв'язку із цим в інженерній практиці широке застосування знаходять непрямі оцінки якості, які характеризують певні якісні показники процеса керування. Вони не є всестороними оцінками якості керування, а визначають лише окремі його сторони.

Кореневі оцінки якості

До непрямих оцінок якості ставляться кореневі, частотні, інтегральні. Розглянемо ті непрямі оцінки, які використаються при рішенні завдань синтезу систем керування.

Перехідна характеристика САУ, по якій визначаються розглянуті вище прямі основні показники якості, є результатом рішення рівняння динаміки. Характер отриманого рішення для системи n-го порядку визначаються власними параметрами, тобто коефіцієнтами рівняння. Однак деякі коефіцієнти рівняння однозначно пов'язані з коріннями характеристичного рівняння, що повністю визначає перехідну складову процесу.

Нагадаємо, що якщо характеристичне рівняння системи n-го порядку має S речовинних виду р_і=-α_і й (n – S) /2 пара комплексних сполучених  корінь типу р_к=- α_до jω_до перехідна складова (складова, що визначає вільний рух системи).

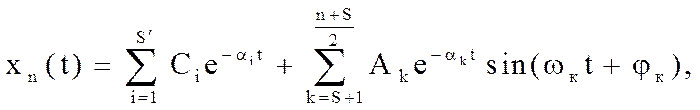
де: С_і, A_к, _до – постійними, обумовленими початковими умовами,

        n - порядок системи.

Наведене вираження свідчить про те, що х_n (t) являє собою суму експонент і сиусоид, кожна з яких  при α_i>0, α_до>0 (у стійких системах).

Неважко прийти до висновку про те, що кожна зі складових убуває тим швидше, чим більше за абсолютним значенням α_i  й α_к. Іншими словами, чим далі розташоване коріння характеристичного рівняння від мнимої осі, тим швидше загасає перехідний процес. При цьому, довше всіх буде загасати складова, обумовлена найближчим до мнимої осі коренем. Саме цим коренем визначається загальний час перехідного процесу системи  цілком.

Відстань до найближчого кореня від мнимої осі називається ступенем стійкості h.

Якщо найближчий до мнимої осі корінь речовинний, то ступінь стійкості аперіодична, якщо пари комплексних сполучених, то ступінь стійкості коливальна.

Зазначена відстань визначає запас стійкості й час загасання процесу, але ніяким образом не відбиває колебательность.

Колебательность процесу визначається наявністю комплексних сполучених корінь і співвідношенням мнимої й речовинної частин цих корінь.

Для оцінки колебательности користуються кореневою оцінкою, називаною ступенем колебательности μ.

Тангенс половинного кута ув'язненого між променями,проведеними з початку координат таким чином, щоб всіх корінь характеристичного рівняння замкнутої системи не виходили за межі площини обмеженої цими променями називається ступенем колебательности  μ.

Розглянемо комплексну площину розташування корінь стійкої системи 5-го порядку.

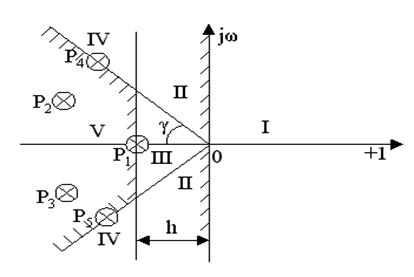Проведемо вертикальну пряму через найближчий до мнимої осі корінь (Р₁) і два промені через комплексних сполучених корінь таким чином, щоб всі коріння перебували в площині, обмеженої цими променями.

Нехай чисельні значення корінь будуть:

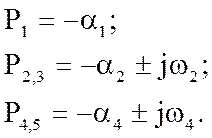
У цьому випадку ступінь стійкості

Ступінь колебательности

μ=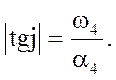

Часто як коренева оцінка колебательности системи використають кореневий показник колебательности .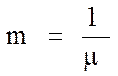

Мнимая вісь, вертикальна пряма й два промені розбиває весь простір можливих значень корінь на 5 областей.

Припустимо, що отримані значення h і м є гранично припустимими. У цьому випадку, область 1, як область розташування корінь для нестійких систем, не може задовольняти необхідною вимогою в плані стійкості.

Розташування корінь в області 2 свідчить про те, що ступінь колебательности перевищує необхідну, а ступінь стійкості менше припустимої, хоча в принципі система стійка.

Знаходження всіх корінь в області 3 забезпечує системі необхідну колебательность, але не задовольняє вимогам припустимого ступеня стійкості.

Область 4 характеризується задоволенням необхідних вимог у забезпеченні заданого ступеня стійкості, але визначає неприпустимо високий ступінь колебательности.

Область 5 - єдина область розташування всіх корінь, що задовольняє  необхідним вимогам у плані забезпечення необхідних як ступеня стійкості, так і ступеня колебательности.

Ця область розташована ліворуч від вертикальної лінії й обмежена двома лугами (границі області заштриховані).

Області із заданими значеннями h й μ можна виділити не тільки в площині розподілу корінь характеристичного рівняння.

Використовуючи D-розбивку на площині двох параметрів  й , можна виділити на цій площині області, у яких забезпечуються задані h й μ.