Другие предметы \ Теория автоматического управления

Теорія лінійних систем. Математичне моделювання лінійних систем керування. Типові динамічні ланки, страница 16

D-розбиття по одному параметру.

            Розбивка простору всіх значень деякого конструктивного параметра γ на області з однаковим розподілом коренів характеристичного рівняння в комплексній площині називається D-розбивкою по одному параметру.

            Якщо необхідно з'ясувати, як впливає на стійкість САУ якийсь конструктивний параметр γ, що лінійно входить у коефіцієнт характеристичного рівняння замкнутої системи, то зазначене рівняння можна представити у вигляді:

Н (р) + γ G (р) = 0,

деН (р) – многочлен, що не містить γ;

G (р) – многочлен, що є співмножником γ.

З цього рівняння знаходимо γ:

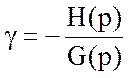
По фізичному змісту γ є дійсним числом, всі можливі його значення розташовуються на числовій осі (лінії). Побудова D-областей зручніше й наочніше проводити на площині, тому параметр γ краще розглядати як якесь комплексне число S =γ+ j λ, у якого дійсна частина γ по суті своїй є величиною, що досліджується.

Тому, після здійснення заміни р=јώ, одержимо γ у вигляді комплексного числа з дійсною частиною U (ω) і уявної V (ω):

γ = - 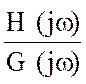 = U (ω) + j (ω).

Для комплексного числа S:

γ = U (ω);

λ = V (ω).

Змінюючи значення ω від - до + , ­­можна розрахувати та відобразити  в комплексній площині величину S у вигляді кривої, яка поділить всю площину на декілька областей, серед яких може знаходитися і область стійкості.


Як конкретний приклад розглянемо систему автоматичного керування

структурна схема якої:


На схемі позначено:

у(р) - завдаючий вплив (завдання);

ε(р) – помилка керування;

μ(р) – керуючий вплив;

х(р) – керована величина;

Кп – коефіцієнт підсилення підсилювача;

Квм – коефіцієнт передачі виконавчого механізму;

Твм – постійна часу виконавчого механізму;

Коб – коефіцієнт передачі об'єкта;

Тоб – постійна часу об'єкта;

р - оператор Лапласа.

Функція передачі замкненої системи:

Ф (р) =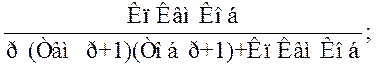

Характеристичне рівняння:

р (Твм р + 1)(Тоб р + 1) + Кп Квм Коб = 0.

Припустимо, що досліджується вплив коефіцієнта підсилення підсилювача Кп на стійкість САУ, тобто, γ = Кп, всі інші параметри відомі.

Розкривши дужки, одержимо:

Твм Тоб р3 + (Твм + Тоб) р2 + р + Кп Квм Коб = 0.

Введемо запропоновані вище позначення:

Н (р) = Твм  Тоб р3 + (Твм + Тоб) р2 +р;

                                          G (р) = Квм Коб

У нашому прикладі, після відповідної постановки одержуємо:

Н (jω) = - (Твм + Тоб) ω2 + jω (1 - Твм Тоб ω2);

                                         G (jω) = Квм Коб;

γ = Кп =

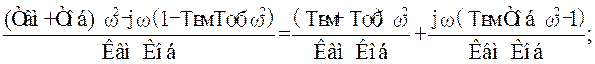
де

U(ω) = 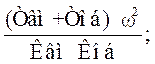      V(ω) =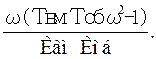


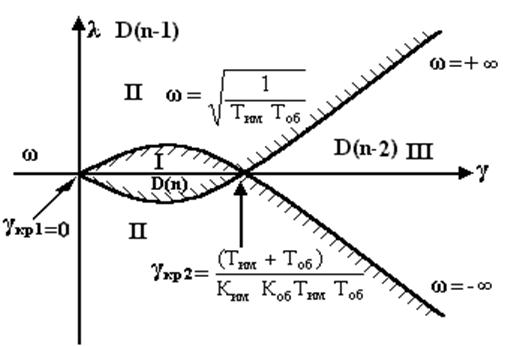При зміні ω від - до + одержуємо числові значення U(ω) і V(ω), використовуючи які, будуємо відповідний графік у комплексній площині.

Отримана крива, що розмежовує всю комплексну площину на три області (I, II, III),  називається основною кривою D-розбиття.

Якщо крива D-розбиттяобмежує деяку область значень параметрів γ, при яких система стійка, то сама крива в  площині параметра γ є межею стійкості.

У площині розподілу коренів  характеристичного рівняння межею стійкості є уявна вісь, яку, з метою наочного відображення необхідного розташування коренів для забезпечення стійкості,  за звичай штрихують ліворуч при зростанні значень ω на цій осі. Тому криву D-розбиттятакож варто заштрихувати ліворуч при збільшенні ω від  - до + .

Із трьох отриманих областей тільки одна (I) має штрихування спрямоване усередину, тому саме для області I кількість корінь у правій напівплощині буде мінімальним; ця кількість може бути не рівною 0, тобто система буде нестійка.

 Для оцінки,  чи є область I областю стійкості, необхідно скористатися будь-яким критерієм стійкості при підстановці в характеристичне рівняння будь-якого значення γ у межах від γ1 до γ2. Якщо виявиться, що система стійка, то область I є областю стійкості. Перехід через криву D-розбиттяіз заштрихованої області в не заштриховану відповідає зменшенню кількості коренів у лівій півплощині на одиницю. В D-області I значення параметра Кп = γ обмежені точками перетину основної кривої D-розбиття з віссю абсцис. У цих точках λ = V(ω)=0, тому:

V(ω) = 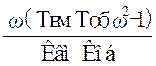=0 при  ω1=0;  ω2,3 = ± ;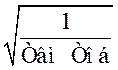

а отже:

γ1 = Кп1 = U(ω1) = 0,

γ2 = Кп2 = U(ω2,3) =.

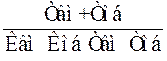У даному прикладі при зміні значень коефіцієнта підсилення підсилювача від Кп1  до Кп2  система стійка.

Визначення області стійкості, тобто D-розбиттяпо одному параметру, можна здійснити й іншими способами, наприклад, скориставшись будь-яким критерієм стійкості.

Так, у нашому прикладі характеристичне рівняння має вигляд:

р(Твм р+1)(Тоб р+1)+КпКвмКоб= Твм Тоб р3+ (Твм+Тоб) р2+ р+ КпКвмКоб= 0,

яке при Кп1 = 0  перетвориться до виду:

р(Твм р+1)(Тоб р+1)=0.

Корені цього рівняння відповідно:

р1=0;   р2 =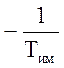 <0;   р3= 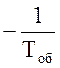<0,

тобто два корені (р2 і р3) розташовані в лівій півплощині комплексної площини, а р1 – на початку координат.

Очевидно, що при Кп1 = 0 система перебуває на межі стійкості, це значення Ку1 є нижнім граничним значенням коефіцієнта підсилення підсилювача.

Верхнє граничне значення Кп2 неважко визначити, скориставшись аналітичним критерієм Вишнєградського. Із цією метою розглянемо  вищенаведене характеристичне рівняння.

Для системи 3-го порядку знаходження САУ на межі стійкості забезпечується при рівності добутків середніх і крайніх коефіцієнтів, тобто:

(Твм+Тоб)1=ТвмТобКп2КвмКоб,

звідки:

Кп2 =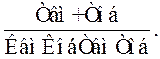

Таким чином, при зміні Кп від 0 до значення 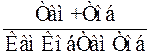 система стійка, що повністю збігається з отриманим вище  результатом D-розбиття при використанні частотного методу.

D-розбиття в площині двох параметрів.

Для побудови області стійкості в площині 2-х параметрів зручно скористатися критерієм стійкості Михайлова.

Будемо  думати, що обоє досліджувані  параметра μ і ν лінійно входять у коефіцієнти характеристичного полінома замкнутої системи.

F(p)=μМ(р) +νN(p)+Z(p)

Скачать файл