![]() – корені рівняння
– корені рівняння ![]() ,
, ![]() .
.
В залежності від виду зображення за Лапласом вихідного сигналу необхідно використовувати той чи інший спосіб отримання перехідної функції. Оберненим перетворенням за Лапласом із заздалегідь визначених таблиць користуються, як правило, коли зображення за Лапласом вихідного сигналу нескладне. А теоремою розкладення користуються, як правило, коли зображення за Лапласом вихідного сигналу являє собою поліном другого, третього або більш високого степеня.
Частотні характеристики типових динамічних ланок
Виконавши в функції передачі W(p) заміну оператора Лапласаp
на ![]() , отримуємо
комплексний коефіцієнт передачі:
, отримуємо
комплексний коефіцієнт передачі:
![]()
Маючи на увазі, що амплітудно-частотна характеристика (АЧХ) ![]() являє собою модуль комплексного
коефіцієнта передачі W(jω) і дорівнює квадратному
кореневі із суми квадратів його уявної та дійсної частин, вона може бути
побудована за виразом:
являє собою модуль комплексного
коефіцієнта передачі W(jω) і дорівнює квадратному
кореневі із суми квадратів його уявної та дійсної частин, вона може бути
побудована за виразом:
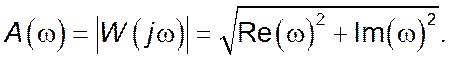
Пам’ятаючи про те, що фазово-частотна характеристика (ФЧХ)![]() є аргумент комплексного коефіцієнта
передачі W(jω) і як для
будь-якого комплексного числа дорівнює арктангенсу відношення уявної та дійсної
частин, то може бути побудована за виразом:
є аргумент комплексного коефіцієнта
передачі W(jω) і як для
будь-якого комплексного числа дорівнює арктангенсу відношення уявної та дійсної
частин, то може бути побудована за виразом:
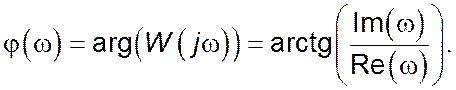
Амплітудно-фазова частотна характеристика будується у комплексній площині
за формулою, якою визначається комплексний коефіцієнт передачі ![]() одним з двох способів: маючи значення
одним з двох способів: маючи значення
![]() і
і ![]() ,
або маючи значення
,
або маючи значення ![]() і
і ![]() .
.
Дійсна частина комплексного коефіцієнту передачі:
![]()
Уявна частина комплексного коефіцієнту передачі:
![]()
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ) здебільшого будується спрощеним способом не як точна, а наближена. Таку характеристику називають асимптотичною ЛАЧХ.
Алгоритм побудови асимптотичної ЛАЧХ полягає в наступному. Спочатку
знаходять розташування вихідної точки А. Для цього потрібно в вибраній системі
координат при ω=1 встановити перпендикуляр до осі абсцис, на якому відкласти
відрізок ОА = 20 lg K, де K – коефіцієнт передачі ланки. Через точку А треба провести пряму лінію
з відповідним кутом нахилу: для простої ланки 0 дВ/дек; для
диференціюючої ланки + 20 дВ/дек; для інтегруючої ланки
–20 дВ/дек. Проведена пряма лінія являє собою ЛАЧХ для
низьких частот, яка при певних значеннях частот змінює кут нахилу. Ці частоти 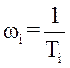 , де Ті – сталі часу
поліномів (Тір+1). При тому, якщо відповідний поліном знаходиться у
чисельнику функції передачі (для ланок з введенням похідної), то кут нахилу збільшується
на 20 дВ/дек, якщо
ж поліном знаходиться у знаменнику (для аперіодичних ланок 1 – го порядку), кут
нахилу зменшується на 20 дВ/дек. У коливальної ланки в знаменнику функції передачі знаходиться поліном 2 – го порядку (Т2р2
+ 2dTp + 1), тому при частоті
, де Ті – сталі часу
поліномів (Тір+1). При тому, якщо відповідний поліном знаходиться у
чисельнику функції передачі (для ланок з введенням похідної), то кут нахилу збільшується
на 20 дВ/дек, якщо
ж поліном знаходиться у знаменнику (для аперіодичних ланок 1 – го порядку), кут
нахилу зменшується на 20 дВ/дек. У коливальної ланки в знаменнику функції передачі знаходиться поліном 2 – го порядку (Т2р2
+ 2dTp + 1), тому при частоті 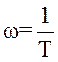 для цієї ланки кут нахилу
вищезгаданої прямої треба зменшити на 40 дВ/дек.
для цієї ланки кут нахилу
вищезгаданої прямої треба зменшити на 40 дВ/дек.
Проста ідеальна ланка
Рівняння динаміки в операційній формі і функція передачі простої ідеальної ланки:
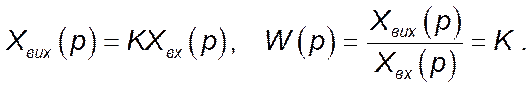
Зображення за Лапласом вхідного сигналу (одиничного стрибка) ![]() :
:
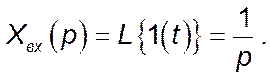
Звідси зображення за Лапласом вихідного сигналу:
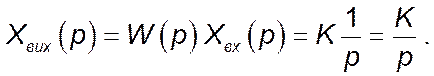
Оригінал вихідного сигналу (перехідну функцію ![]() )
можна знайти, користуючись оберненим перетворенням за Лапласом із заздалегідь
визначених таблиць:
)
можна знайти, користуючись оберненим перетворенням за Лапласом із заздалегідь
визначених таблиць:
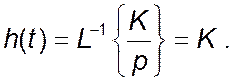
Перехідна характеристика зображена на рисунку. Вона являє собою пряму лінію, яка розташована паралельно осі абсцис на відстані K від неї.
 |
![]()
Амплітудно-частотна характеристика ![]() може
бути побудована за виразом:
може
бути побудована за виразом:
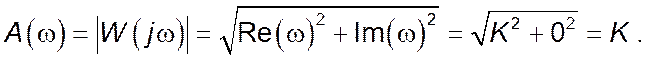
Фазово-частотну характеристику ![]() можна
побудувати за виразом:
можна
побудувати за виразом:
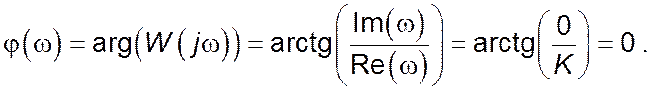
Амплітудно-фазова частотна характеристика будується у комплексній площині
за формулою, якою визначається комплексний коефіцієнт передачі ![]() одним з двох способів: маючи значення
одним з двох способів: маючи значення
![]() і
і ![]() ,
або маючи значення
,
або маючи значення ![]() і
і ![]() .
.
Дійсна частина комплексного коефіцієнту передачі:
![]()
Уявна частина комплексного коефіцієнту передачі:
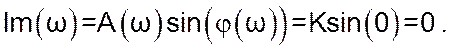

Амплітудно-частотна характеристика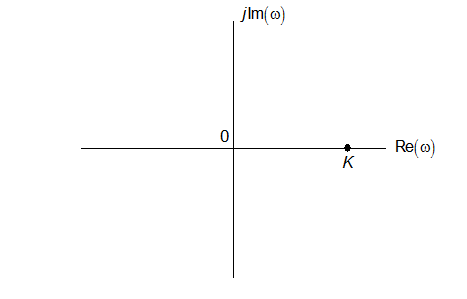
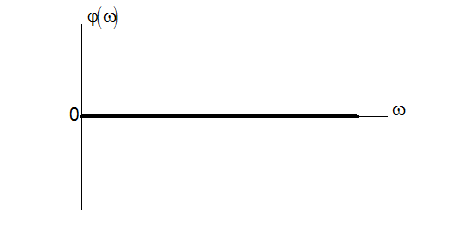 Фазово-частотна
характеристика
Фазово-частотна
характеристика
Амплітудно-фазова частотна характеристика
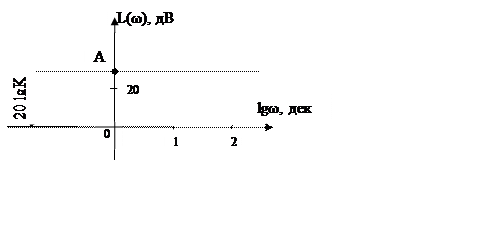
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ) описується виразом: L(ω) = 20lgK, являє собою горизонтальну пряму лінію, яка зміщена відносно осі абсцис на величину 20lgK.
Ідеальна інтегруюча ланка
Рівняння динаміки в операційній формі і функція передачі ідеальної інтегруючої ланки:
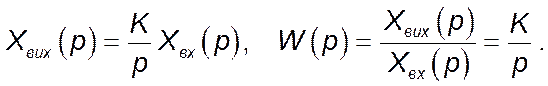
Зображення за Лапласом вхідного сигналу ![]() :
:
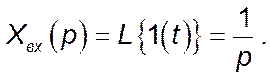
Звідси зображення за Лапласом вихідного сигналу:
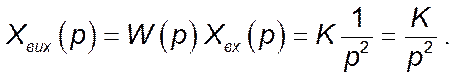
Перехідну функцію ![]() можна знайти,
користуючись оберненим перетворенням за Лапласом із заздалегідь визначених
таблиць:
можна знайти,
користуючись оберненим перетворенням за Лапласом із заздалегідь визначених
таблиць:
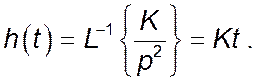
Перехідна характеристика зображена на рисунку. Вона являє собою пряму
лінію, яка виходить з початку координат і розташована під кутом ![]() до осі абсцис.
до осі абсцис.
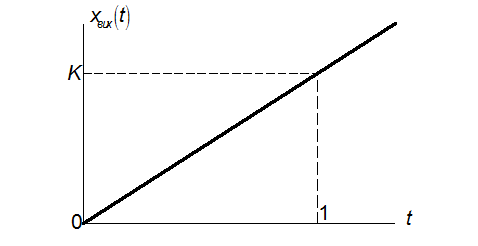
Виконавши заміну p на ![]() , отримаємо
комплексний коефіцієнт передачі:
, отримаємо
комплексний коефіцієнт передачі:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.