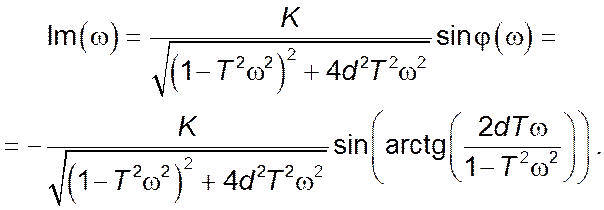
 |
 |
|
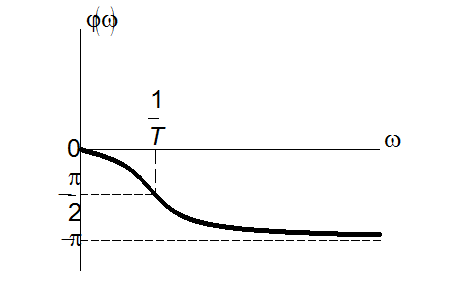
Фазово-частотна характеристика
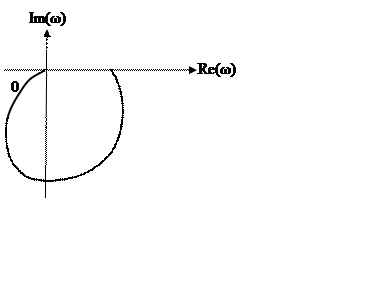 |
Амплітудно-фазова частотна характеристика
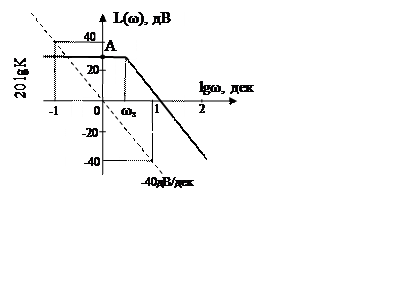
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ) простої
коливальної ланки описується виразом L(ω) = 20lgK-20lg![]() , являє собою ламану
лінію, яка горизонтально проходить через точку А[0; 20lgK], а при частоті
, являє собою ламану
лінію, яка горизонтально проходить через точку А[0; 20lgK], а при частоті 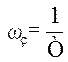 змінює кут нахилу
зразу на -40 дВ/дек і при високих частотах має кут нахилу -40 дВ/дек.
змінює кут нахилу
зразу на -40 дВ/дек і при високих частотах має кут нахилу -40 дВ/дек.
Ланка чистого запізнення
Рівняння динаміки і функція передачі ланки чистого запізнення в операційній формі мають вигляд (де t – час чистого запізнення):
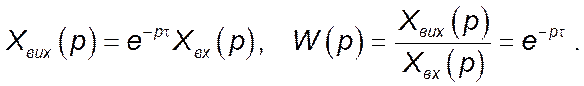
Зображення за Лапласом вхідного сигналу ![]() :
:
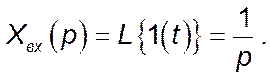
Звідси зображення за Лапласом вихідного сигналу:
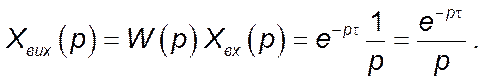
Оригінал вихідного сигналу можна знайти, користуючись оберненим перетворенням за Лапласом із заздалегідь визначених таблиць:
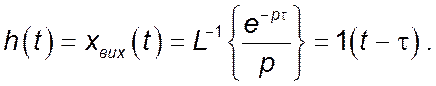
Перехідна характеристика зображена на рисунку.

Виконавши заміну p на ![]() , отримаємо
комплексний коефіцієнт передачі (користуючись формулою Ейлера):
, отримаємо
комплексний коефіцієнт передачі (користуючись формулою Ейлера):
![]()
Амплітудно-частотна характеристика ![]() :
:
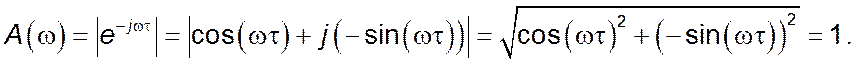
Фазово-частотна характеристика ![]() :
:
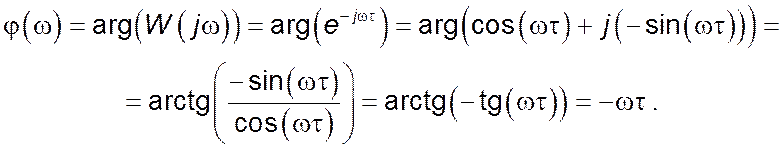
Дійсна частина комплексного коефіцієнту передачі:
![]()
Уявна частина комплексного коефіцієнту передачі:
![]()

Амплітудно-частотна характеристика
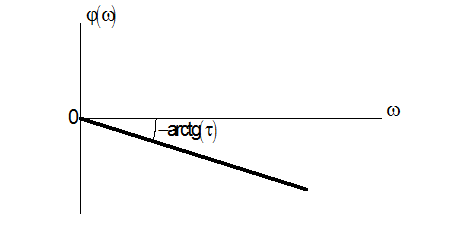
Фазово-частотна характеристика
 |
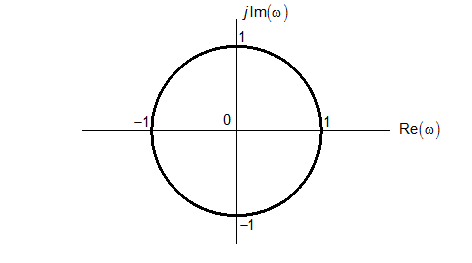
Амплітудно-фазова частотна характеристика
Логарифмічна амплітудно-частотна характеристика (ЛАЧХ)
Амплітудно-фазова частотна характеристика ланки чистого запізнення являє собою коло одиничного радіуса.
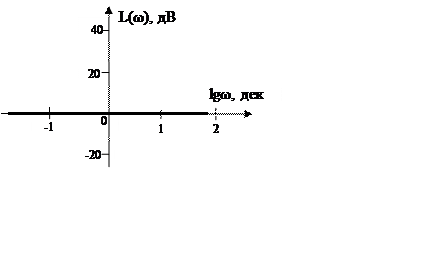
Оскільки А(ω)=1, то логарифмічна амплітудно-частотна
характеристика (ЛАЧХ) ланки
чистого запізнення L(ω) = 0 і являє собою пряму лінію, яка співпадає
з віссю абсцис.
Види з’єднань динамічних ланок.
Утворюючи ту чи іншу систему автоматичного керування, динамічні ланку можуть бути з’єднані між собою різними способами. Розрізняють послідовне та паралельне з’єднання. При послідовному з’єднанні вхідний сигнал послідовно проходить через всі ланки. При паралельному з’єднанні можливі два варіанти: перший, коли один вхідний сигнал подається на входи всіх ланок, а всі їхні вихідні сигнали додаються на суматорі (прямий зв'язок), другий, коли вихідний сигнал якоїсь ланки, або певна його частина, знову проступає на її вхід (зворотний зв’язок). При тому, цей сигнал може додаватися до основного або відніматися (відповідно додатний або від’ємний зворотний зв'язок).
Розглянемо визначення еквівалентної функції передачі структури при послідовному з’єднанні динамічних ланок:
Значення функцій передачі окремих ланок:
 |

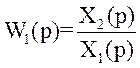 ;
; 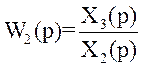 ;
; 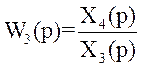 .
.
Еквівалентна функція передачі всієї структури при послідовному з’єднанні
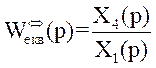 .
.
Якщо чисельник та знаменник одночасно помножити на Х2(р), Х3(р), то отримаємо:
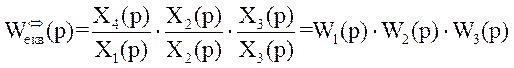 ,
,
тобто, при послідовному з’єднанні динамічних ланок еквівалентна функція передачі такої структури дорівнює добутку функцій передачі окремих елементів:
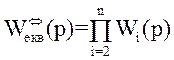 .
.
При паралельному з’єднанні (прямий зв’язок) структурна схема виглядає так:
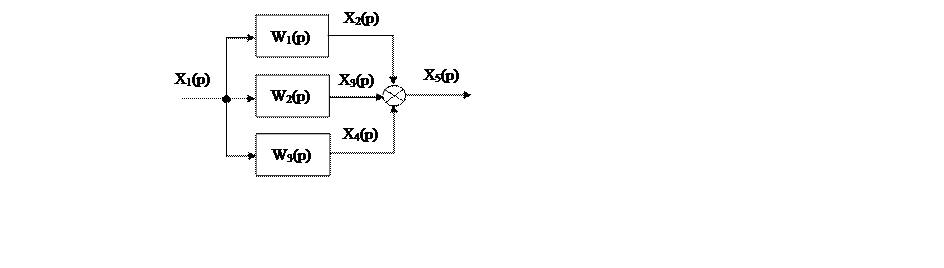
Вихідний сигнал структури являє собою суму вихідних сигналів окремих ланок:
Х5(р) = Х2(р) + Х3(р) + Х4(р),
а еквівалентна функція передачі такої структури:
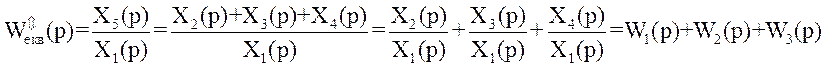 ,
,
іншими словами при паралельному з’єднанні еквівалентна функція передачі дорівнює сумі функцій передачі окремих елементів:
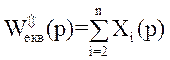 .
.
При зворотному зв’язку, де одна ланка охоплює зворотним зв’язком іншу, структурна схема має вигляд:
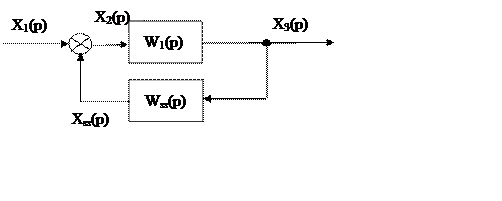 |
Еквівалентна функція передачі такої структури :
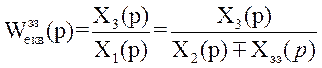 .
.
Поділивши чисельник і знаменник на Х3(р), отримаємо:
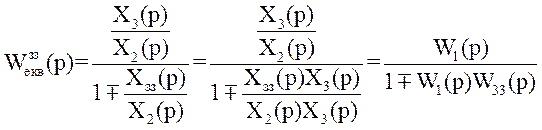 .
.
В останній формулі знак «плюс» вибирається для від’ємного зворотного зв’язку, а «мінус» для додатного. Таким чином, при наявності зворотного зв’язку еквівалентна функція передачі являє собою дріб, в чисельнику якої записана функція передачі ланки, яка охоплена зворотним зв’язком, а у знаменнику функція передачі ланки, яка її охоплює.
Різновиди функцій передачі систем керування.
Розглянемо просту одноконтурну систему, яка складається з об’єкта керування та керуючої частини.
 |
Wзб(p) – функція передачі об’єкта керування по каналу збурення;
Wоб(p) – функція передачі об’єкта керування по каналу керування;
Wкч(p) – функція передачі керуючої частини;
f(p) – збурення;
Y(p) – завдаючий вплив (завдання);
U(p) – керуючий вплив;
Х(р) – координата стану об’єкта керування;
ε(р) = Y(p) - Х(р) – помилка керування;
В запропонованій системі можна виділити дві вхідних дії: завдання Y(p) та збурення f(p) і дві вихідних координати – координату стану об’єкта Х(р), помилку керування ε(р).
Функція передачі за визначенням може бути записана тільки для однієї вхідної та однієї вихідної величини, при тому вважають, що інші вхідні величини відсутні, тобто дорівнюють нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.