Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы

Министерство образования и науки Российской федерации

Федеральное агентство по образованию

Саратовский государственный технический университет

Балаковский институт, техники, технологии и управления

МОДЕЛИРОВАНИЕ СИСТЕМ НА МИКРОУРОВНЕ

Методические указания к выполнению курсовой работы

по дисциплине «Моделирование систем» для студентов специальности 220201 заочной формы обучения

Одобрено

редакционно-издательским советом

Балаковского  института техники,

технологии и управления

Балаково 2010

- овладение навыками расчетов согласно теории систем с распределенными параметрами;

- знакомство с уравнениями и специальными функциями математической физики.

УКАЗАНИЯ ПО СОСТАВЛЕНИЮ И ОФОРМЛЕНИЮ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ

В расчетно-пояснительной записке даются подробные данные к работе и отражают все пункты задания на курсовую работу. Рекомендуется следующее содержание расчетно-пояснительной записки:

Введение

1. Исходные данные.

2. Постановка краевой задачи.

3. Расчет выходной распределенной величины:

4. Оценка динамических свойств объекта моделирования

                Заключение                                                                                                       

Список использованных источников                                                            

Приложение А                                                                                                 

Пояснительная записка должна быть выполнена на листах формата А4, с большим штампом на первом листе и малыми на последующих в соответствии со следующими требованиями.

1) Оформление основного текста:

- Формат шрифта - Times New Roman,

- Размер шрифта – 14;

- Интервал полуторный;

- Выравнивание – по ширине;

- Отступ – 1,25.

2) Оформление заголовков:

- Заголовки разделов печатаются заглавными буквами, номер раздела без точки, выравнивание по ширине с отступом 1,25. Каждый раздел начинается с нового листа.

- Содержание, введение, заключение, список используемых источников заглавными буквами по центру.

- Заголовки подпунктов выполняется строчными буквами. Точка ставится только после указания раздела, к которому относится подпункт. Заголовок подпункта в тексте выделяется пробелами. Исключение составляет, когда подпункт идет сразу после наименования раздела.

- После всех заголовков точка не ставится.

3) Оформление таблиц: таблицы необходимо сопровождать тематическими заголовками, иметь свой номер со сквозной нумерацией.

4) Рисунки должны иметь сквозную нумерацию с тематическим заголовком.

5) Оформление Приложения с графической частью согласно приложениям данного методического указания.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1 Основы теории систем с распределенными параметрами

Модели на микроуровне описываются дифференциальными уравнениями с частными производными, а объекты моделирования представляют собой системы с распределенными параметрами (СРП), состояние которых описывается функциями нескольких аргументов, зависящих как от времени, так и от пространственных координат. Пространственно-временными характеристиками описываются физические поля различной природы: электромагнитное и температурное поле, поля деформаций, скоростей, давлений и т.д.

В качестве наглядного примера рассмотрим процесс сушки и перемещения сырья на ленточном конвейере (рис.1.1).

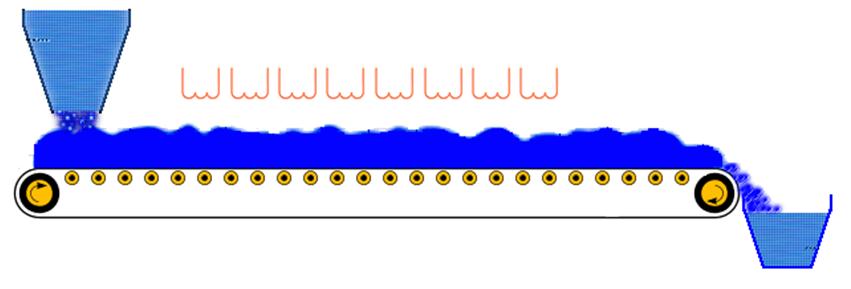
Рис.1.1 - Процесс сушки и перемещения сырья на ленточном

                конвейере

В процессе сушки нагревателями, установленными сверху, материал неравномерно прогревается как по высоте на одном и том же сечении, так и по длине конвейера. Поэтому в данном случае, описывая температуру сырья необходимо говорить о системе с распределенными параметрами, так как температуры материала зависит как от времени t, так и от пространственных координат (х и у).

          Рассматривая техническое устройство, его также можно представить в виде системы, состоящей из множества взаимосвязанных элементов. При этом один или несколько элементов могут являться объектами с распределенными параметрами. Например, мембрана или струна соответственно в мембранных или струнных датчиках.   

На практике состояние любого технического объекта управления в силу конечных геометрических размеров описывается функцией Q(x,t), зависящей как от времени t, так и от вектора пространственных координат х. В том случае, если зависимость функции Q от х пренебрежимо мала, то такой объект может рассматриваться как система с сосредоточенными параметрами (ССП) и рассматриваться с позиции ТАУ. В противном случае применение методов ТАУ к СРП может привести к существенным погрешностям и потерям качественных особенностей функционирования объекта (системы).

Основным отличием СРП от ССП заключается в используемом математическом аппарате:

– СРП описываются дифференциальными уравнения в частных производных (ДУЧП);

– ССП описываются обыкновенными дифференциальными уравнениями.

Далее описаны основные модели объектов и систем управления с распределенными параметрами, на основании методики, изложенных Бутковским и Рапопорт [6,15].

1.1 Базовые уравнения систем с распределенными параметрами

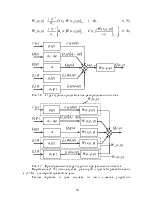
Большинство распределенных объектов описывается уравнением вида:

  ,                                                                                                                 (1.1)

где     Q(x,t) - функция состояния (выход объекта СРП);

D – открытая часть замкнутой области Ď, не содержащая границ;

f(x,t) – известная функция, характеризующая внешнее воздействие

              на процесс (вход объекта СРП);

L – некоторый заданный оператор.

Оператор  L может представлять собой:

– линейную функцию Q;

– частные производные от Q по х и t различных порядков;

– интегральный оператор Q по х и t.

Конкретный вид определяется содержанием описываемого процесса.

Если f(x,t) =0, то уравнение (1.1) называется однородным.

Если f(x,t) ≠0, то уравнение - неоднородное.

Для получения единственного решения уравнение (1.1) надо дополнить начальными условиями, которые описываются некоторым линейным оператором следующего вида:

x  Ď, t=0,                                                                                                                        (1.2)

где     Q₀(x) – начальная функция, описывающая искомую функцию Q в

                      замкнутой области Ď в начальный момент времени t=0.

Если Q₀(x)=0, то начальные условия (1.2) называются нулевыми, иначе – ненулевыми.

Условие (1.2) необходимо, но недостаточно для выделения единственного решения (1.1), что является принципиальной особенностью СРП по сравнению с системой сосредоточенными параметрами (ССП). Полная система соотношений должна содержать граничные условия для Q(x,t), которые характеризуют взаимодействие Q(x,t) с внешней средой для момента времени  на границе области ∂Ď. Граничные условия в общем виде описываются выражением: