Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 10

f(x,t) – объёмная плотность источника примеси, кг·м^-3·с^-1.

При условии постоянства коэффициента диффузии D коэффициент а определяется из выражения:

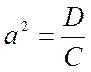,                                                                                               (2.58)

где     D – коэффициент диффузии, м²/с;

          C – коэффициент пористости.

          Коэффициент пористости можно рассчитать следующим образом:

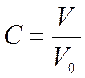,                                                                                                (2.59)

где     V – объем пор, внутри которых может происходить диффузия, м³;

          V₀ – полный объем, м³.

Если среда не пористая, то коэффициент С=1, а коэффициент а²=D.

В качестве начальных условий задается распределение плотности диффундирующего вещества вдоль рассматриваемой полой трубки в начальный момент времени:

.                                                                         (2.60)

Граничные условия могут быть заданы в следующей форме [18, с.25]:

1) На границах полой трубки концентрация диффундирующего вещества поддерживается постоянной (в частности равной нулю) (граничные условия 1 рода):

;                                                                          (2.61)

.                                                                          (2.62)

2) Граничные плоскости трубки непроницаемы (граничные условия 2 рода):

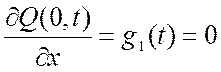;                                                                             (2.63)

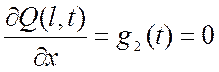.                                                                             (2.64)

3) Граничные плоскости полунепроницаемы, причем диффузия через эти плоскости происходит по закону Ньютона для конвективного теплообмена (граничные условия 3 рода):

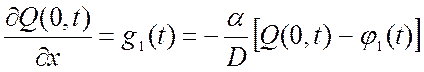,                                                (2.65)

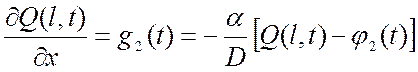,                                               (2.66)

где     φ₁(t), φ₂(t)  – плотность диффундирующего вещества в окружающей среде по оба конца трубки;

          α – коэффициент проницаемости на концах.

Пример.

Поставить краевую задачу для процесса диффузии взвешенных частиц с учетом оседания, предполагая, что скорость частиц, вызываемая силой тяжести, постоянна, а плотность частиц зависит только от высоты z и от времени t. Записать граничное условие, соответствующее непроницаемой перегородке.

Функция Q(x,t), описывающая плотность взвешенных частиц в трубке определяется уравнением:

,

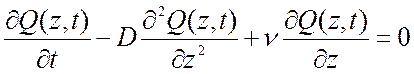где     z>0;

t>0;

D – коэффициент диффузии, м²/с;

ν – скорость оседания частиц, м/с.

Граничное условие сформулированному условию записывается в виде:

.

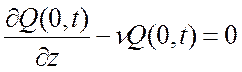2.7 Уравнения линий передач

Рассмотрим кабель длиной l, находящийся под током. Кабель имеет следующие параметры, отнесенные к единице длины провода:

– активное сопротивление R, Ом/м;

– индуктивность L, Гн/м;

– емкостное сопротивление C, Ф/м;

– проводимость изоляции G, (Ом·м)^-1.

Напряжение U и ток I в каждый момент времени t в любой точке х могут быть найдены из следующих уравнений:

 1) Уравнение телефона:

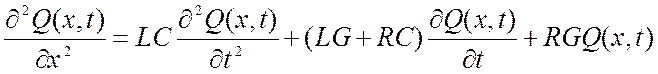,                  (2.67)

где     Q(x,t)=U(x,t) или Q(x,t)=I(x,t).

2) Уравнение телеграфа (телеграфное уравнение) при условии пренебрежимо малых значений индуктивности и проводимости L=G=0:

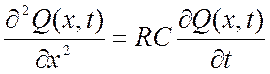.                                                                      (2.68)

3) Уравнение радио (при малых значениях активного сопротивления и проводимости R=G=0):

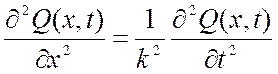,                                                                     (2.69)

где     k²=1/(LC).

Во всех уравнениях в качестве выходной распределенной величины могут рассматриваться как напряжение U(x,t), так и ток I(x,t).

Для уравнений телефона и радио, которые содержат вторую производную по времени t, необходимо задание начальных условий в виде самой распределенной величины в начальный момент времени вдоль всей линии, так и ее производной по времени t. Рассмотрим их расчет.

Пусть вдоль линии задано распределение напряжения и тока:

;                                                                      (2.70)

.                                                                       (2.71)

Тогда:

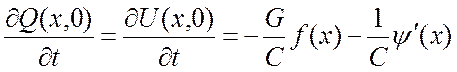;                                              (2.72)

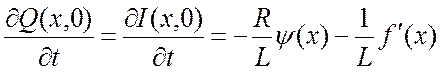.                                             (2.73)

Граничные условия могут задаваться в различных вариантах. Рассмотрим самые распространенные, для одного из конца кабеля (линии), например х=l.

1) На конце включена батарея с постоянной электродвижущей силой Е, В:

.                                                                             (2.74)

2) Конец линии находится под синусоидальным напряжением с частотой ω:

.                                                                  (2.75)

3) Конец линии заземлен:

.                                                                              (2.76)

4) Конец провода изолирован:

.                                                                                (2.77)

5) В начале и в конце линии включены приемники с омическим сопротивлением R₀ и  R_l  и самоиндукцией L₀ и L_l:

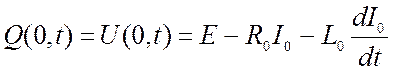;                                                    (2.78)

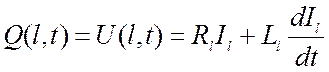,                                                             (2.79)

где     Е – электродвижущая сила батареи, В;

          I₀, I_l – сила тока в начале и в конце линии, А.

6) В начале и в конце линии включены разделительные конденсаторы емкостью С₀ и С_l:

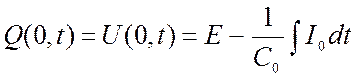;                                                         (2.80)

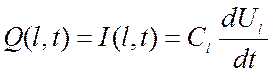,                                                                     (2.81)

где     U_l – напряжение на конце линии.

Пример 1.

Линия передачи длиной 1000 км находится изначально в установившемся режиме с потенциалом 1200 В на передающем конце (х=0) и 1100 В на приемном конце (х=l=1000). Приемный конец линии внезапно заземляется, а на источнике сохраняется потенциал 1200 В. Сформулировать краевую задачу для потенциала  в линии передач, предполагая индуктивность и проводимость изоляции пренебрежимо малыми.

Так как L=G=0, используем телеграфное уравнение вида:

,

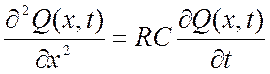где     0≤х≤ 1000.

Начальные  условия (начальное установившееся напряжение) описываются уравнением вида:

.

Граничные условия задаются в виде:

, .

Пример 2.

Найти силу тока I(x,t) в проводе длиной l, по которому течет переменный ток, если утечка тока отсутствует, а омическим сопротивлением и проводимостью можно пренебречь. Предполагается, что начальный ток в проводе (при t=0) равен нулю, а начальное напряжение задается формулой: