Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 16

Для однородного цилиндра длиной l, равномерно нагретого в начальный момент времени, поставить краевую задачу об определении его температуры. При этом его торцы считать теплоизолированными, на внутренней поверхности происходит конвективный теплообмен по закону Ньютона с окружающей средой нулевой температуры, а на внешней – с окружающей средой, температура которой изменяется по косинусоидальному закону.

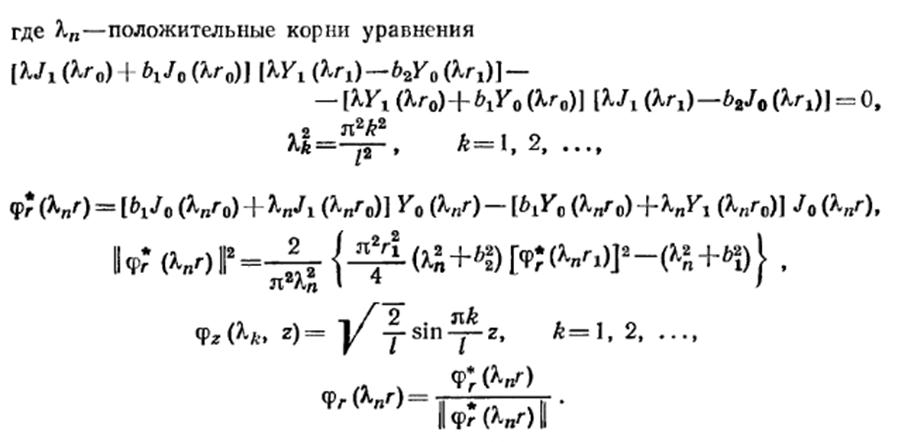
Примечание.

          В качестве расширенного задания (по желанию) осуществить моделирование рассматриваемого процесса с использование программного продукта Elcut. Его бесплатная студенческая версия распространяется свободно в сети Интернет. Справочная система (русская, как и вся программа) содержит все необходимые теоретические сведения и подробные алгоритмы построения моделей и их исследования. Пример такого моделирования приведен на образце Плаката №3.

ЛИТЕРАТУРА

1.  Бицадзе А.В. Сборник задач по уравнениям математической физики. / А.В.Бицадзе,  Д.Ф.Калиниченко. 2-е изд., доп. – М. Наука, 1985. – 312 с.

2. Боголюбов А.Н. Задачи по математической физике: учеб. пособие. – М.: изд-во МГУ, 1998. – 350с.
3.  Будак Б.М. Сборник задач по математической физике: Учеб. пособие/ Б.М.Будак, А.А.Самарский, А.Н.Тихонов. - 4-е изд. - М.: Физматлит, 2004. - 688 с.

4.  Бутковский А.Г. Методы управления системами с распределенными параметрами. / А.Г.Бутковский. – М.: Наука, 1975. – 568 с.

5.  Бутковский А.Г. Структурная теория распределенных систем. / А.Г.Бутковский. – М.: Наука, 1977. – 320 с.

6.  Бутковский А.Г. Характеристики систем с распределенными параметрами. / А.Г.Бутковский. – М.: Наука, 1979. – 224 с.

7.  Власов В.В. Физика в уравнениях математической физики / Доклады 5 Рос. науч.конференции «Векторная энергетика в технических, биологических и социальных системах», Саратов, СООО «АН ВЭ», 2002, с.3-11

8.   Кузнецов А.В. Методы математической физики: Учеб. пособие / Яросл. гос. ун-т. - Ярославль, 2004. – 200с.

9.   Мефедова Ю.А. Моделирование систем управления: Учебно-методическое пособие. – Саратов: СГТУ, 2011.

10.  Полянин А.Д. Справочник по линейным уравнениям математической физики. /А.Д.Полянин. – М.: Физматлит, 2001. – 576с.

11.  Рапопорт Э.Я. Анализ и синтез систем автоматического управления с распределенными параметрами: Учеб. пособие / Э.Я.Рапопорт. – М.: Высш.шк., 2005. – 292 с.: ил.

12.  Сборник задач по уравнениям математической физики. / под ред. В.С.Владимирова. – 3-е изд., исправл. – М.:Физматлит, 2001. – 288 с.

13. Тихонов А.Н., Самарский А.А. Уравнения математической физики: Учеб. пособие для ун-тов.- 4-е изд., испр.- М.:Наука, 1972.- 735 с

ПРИЛОЖЕНИЯ

1 Пример оформления листа перед графической частью с примерным наименованием плакатов.

ПРИЛОЖЕНИЕ А

(обязательное)

Графическая часть

1 Исходные данные и идентификация краевой задачи                             

2 Расчёт статической характеристики                                                        

3 Расчёт динамической характеристики                                                    

2 Примерный вид плакатов

3 Свойства дельта-функции при вычислении интегралов

Вид стандартизирующей функции со всеми возможными комбинациями:

Общее решение для расчета выходной распределенной величины:

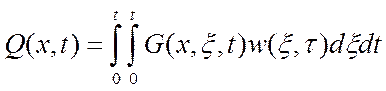
Составляющие решения:

4 Таблица интегралов, производных и преобразований лапласа

Функция	Производная	Интеграл

	1

СОДЕРЖАНИЕ

УКАЗАНИЯ ПО СОСТАВЛЕНИЮ И ОФОРМЛЕНИЮ ЗАПИСКИ

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1 Основы теории систем с распределенными параметрами

1.1 Базовые уравнения систем с распределенными параметрами

1.2 Уравнения гиперболического типа

1.3 Уравнения параболического типа

1.4 Уравнения эллиптического типа

1.5 Начальные условия в краевой задаче 

1.6 Граничные условия в краевой задаче 

1.7 Основное соотношение «вход – выход»

1.8 Функция Грина

1.9 Стандартизирующая и передаточная функции

1.10 Типовые распределенные блоки

1.11 Структурное моделирование распределенного блока

2 Основные уравнения математической физики

2.1 Уравнения поперечных колебаний струны

2.2 Уравнения продольных колебаний стержня

2.3 Уравнения крутильных колебаний стержня

2.4 Уравнение колебаний мембраны

2.5 Уравнение распределения температуры в стержне

2.6 Уравнение диффузии

2.7 Уравнения линий передач

Вопросы для самопроверки.

ПРИМЕР ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ

1 Исходные данные

2 Постановка краевой задачи

3 Расчёт выходной распределенной величины

4 Оценка динамических свойств объекта моделирования

ВАРИАНТЫ ЗАДАНИЙ

ЛИТЕРАТУРА

ПРИЛОЖЕНИЯ

1 Пример оформления листа перед графической частью

2 Примерный вид плакатов

3 Свойства дельта-функции при вычислении интегралов

4 Таблица интегралов, производных и преобразований Лапласа

МОДЕЛИРОВАНИЕ СИСТЕМ НА МИКРОУРОВНЕ

Методические указания к выполнению курсовой работы

по дисциплине «Моделирование систем» для студентов специальности 220201 заочной формы обучения

Составил:             Мефедова Юлия Александровна

                                        Рецензент             Т.Н. Скоробогатова

Редактор              

Корректор           

Подписано в печать		Формат 60х84 1/16
Бумага   тип.	Усл. печ. л. 2,5	Уч.-изд.л. 2,5
Тираж    100     экз.	Заказ	Бесплатно

Саратовский государственный технический университет

410054, г.Саратов, ул.Политехническая, 77

Копипринтер БИТТиУ, 413840, г.Балаково, ул. Чапаева, 140