Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 15

1	;     ;   a > 0
2	,
3	,
4
5	, μn – положительные корни уравнения:
6

Вариант 2.9

Пусть стержень длиной lпогружают в горячую воду до тех пор, пока температура во всех его точках не достигнет 80⁰С. В момент времени t=0 его боковую поверхность теплоизолируют, а его оба конца вставляют в лед при 0⁰С. Сформулировать и решить краевую задачу для вычисления температуры стержня после выполнения сформулированных условий.

1	;     ;   a ≠ 0
2
3
4
5
6

Вариант 2.10

Поставить и решить краевую задачу определения температурного поля одномерного однослойного шара радиусом R. В начальный момент времени температурное поле подчиняется закону F(r). Шар помещен в среду, температура которой изменяется по синусоидальному закону, при этом теплообмен на поверхности подчиняется закону Ньютона.

1	;     ;   a ≠ 0;
2
3
4
5	, μk – расположенные в порядке возрастания положительные корни уравнения:
6

Вариант 2.11

Для тонкого однородного стержня длиной l, равномерно нагретого в начальный момент времени и теплоизолированного на боковой поверхности, поставить и решить краевую задачу об определении его температуры. При этом температура на одном его конце х=0 поддерживается постоянной и равной начальной температуре, а на другом его конце х= l происходит конвективный теплообмен по закону Ньютона с окружающей средой, температура которой изменяется по синусоидальному закону.

Вариант 2.12

Линия передачи длиной 800 км находится изначально в установившемся режиме с потенциалом 6100 В на передающем конце (х=0) и 6000 В на приемном конце (х=l=1000). Приемный конец линии внезапно заземляется, а на источнике сохраняется потенциал 6100 В. Сформулировать краевую задачу для потенциала  в линии передач, предполагая индуктивность и проводимость изоляции пренебрежимо малыми.

1	;     ;   a ≠ 0
2
3
4
5
6

Вариант 2.13

Найти силу тока I(x,t) в проводе длиной l, по которому течет переменный ток, если утечка тока отсутствует, а омическим сопротивлением и проводимостью можно пренебречь. Предполагается, что начальный ток в проводе (при t=0) равен нулю, а начальное напряжение задается формулой:

.

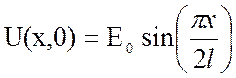Левый конец провода (х=0) изолирован, а правый конец (х=l) заземлен.

1	, ,  a ≠ 0
2	,
3	,
4
5
6

Вариант 2.14

Сформулировать и решить краевую задачу о колебаниях однородной струны (0<x<l), закрепленной на одном конце и свободной на другом, под действием внешней непрерывно распределенной силы с плотностью g(x,t)=Asin(ωt), где ω≠(kπa/t) (k=1,2…). Начальное отклонение струны принять нулевым, а начальную скорость равной некоторой заданной величине.

1	, ,  a ≠ 0
2	,
3	,
4
5
6

Вариант 2.15

Сформулировать и решить краевую задачу о вынужденных колебаниях прямоугольной мембраны (0≤х≤l₁, 0≤y≤l₂), если в начальный момент времени t=0 отклонение точек мембраны от плоскости xOy равно нулю, а ее начальная скорость некоторой заданной величине. Мембрана закреплена неподвижно на плоскостях (0,у) и (х,0) и свободна на других плоскостях. Внешнее воздействие на мембрану описывается плотностью силы g(x,y,t)=A·sin(B·t).

1	;     ;    ;   a > 0
2	Q(x,y,0) = Q0(x,y);
3	Q(0,y,t) = g1 (у,t);          ;         ;
4
5	;;;
6

Вариант 2.16

Сформулировать и решить краевую задачу о вынужденных колебаниях прямоугольной мембраны (0≤х≤l₁, 0≤y≤l₂), если в начальный момент времени t=0 отклонение точек мембраны от плоскости xOy равно нуля, а ее начальная скорость некоторой заданной величине. Мембрана закреплена неподвижно на плоскостях (0,у) и (l₁,y) и свободна на других плоскостях. Внешнее воздействие на мембрану описывается плотностью силы g(x,y,t)=A·sin(B·t).

1	;     ;    ;   a > 0
2	Q(x,y,0) = Q0(x,y);
3	Q(0,y,t) = g1 (у,t);          Q(l1,y,t) = g2 (y,t); ;         ;
4
5	; ;   ;
6

Вариант 2.17

Поставить и решить краевую задачу определения температурного поля диска радиусом R. В начальный момент времени диск нагрет равномерно. На радиусе R температура диска изменяется по синусоидальному закону Θ·sin(D·t). Боковая поверхность диска теплоизолирована.

1	;     ;   a ≠ 0
2
3	,
4
5
6

Вариант 2.18

Поставить и решить краевую задачу определения температурного поля диска радиусом R. В начальный момент времени температурное поле диска подчиняется закону F(r). На радиусе R температура диска поддерживается неизменной и равной Θ. Внешнее воздействие на диск описывается синусоидальным законом А·sin(D·t).

1	;     ;   a ≠ 0
2
3
4
5	, μk – положительные корни уравнения:
6

Вариант 2.19

Сформулировать и решить краевую задачу о вынужденных колебаниях кольцевой мембраны, упруго закрепленной на внешнем и внутреннем радиусах под действием внешней плотности силы g(r,t)=A·sin(B·t). В начальный момент времени смещения кольцевой мембраны отсутствует, но она обладает некоторой заданной начальной скоростью.

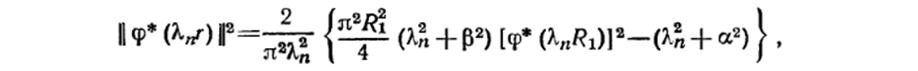
Вариант 2.20