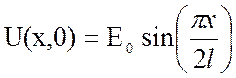Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 11

.

Левый конец провода (х=0) изолирован, а правый конец (х=l) заземлен.

Так как R=G=0 выбираем уравнение радио:

,

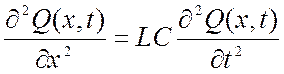где     Q(x,t)=I(x,t) – распределенная токовая величина;

          L – индуктивность, приведенная к единице длины, Гн/м;

          C – емкость, приведенная к единице длины, Ф/м.

          Начальные условия имеют вид:

,

.

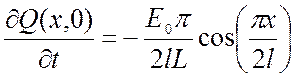          Граничные условия задаются в виде:

,

.

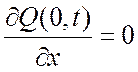Описанные примеры формулировок краевых задач могут быть использованы для постановки собственных задач.

Далее рассмотрен пример выполнения моделирования объекта в распределенных параметрах.

Вопросы для самопроверки.

1) Как записывается краевая задача в общем виде?

2) Что называется начальной функцией?

3) Что описывают граничные условия?

4) Как по внешнему виду определить уравнения гиперболического, параболического и эллиптического типов?

5) Какие процессы описывают уравнения гиперболического, параболического и эллиптического типов?

6) Какие начальные условия записывают для уравнения гиперболического типа?

7) Как выглядят начальные условия для уравнений эллиптического типа?

8) Как записываются граничные условия для первой, второй и третьей краевых задач?

9) Что собой представляет функция Грина и стандартизирующая функция?

10) Какие выделяют типовые распределенные блоки?

11) Как рассчитывается передаточная функция паралелльно соединенных блоков?

12) Почему последовательное соединение называется некоммутативным?

ПРИМЕР ВЫПОЛНЕНИЯ КУРСОВОЙ РАБОТЫ

1  Исходные данные

Поставить и решить краевую задачу для колебания струны, жестко закрепленной на концах под действием внешней силы плотностью А·sin (Bt). Считать, что в начальный момент времени струна выпуклая (описывается синусоидальным законом), а начальная скорость нулевая.

1	, , ,  a ≠ 0
2	,
3	,
4
5
6

Примечание: Размеры, материал моделируемого объекта выбираются самостоятельно. Также определяются самостоятельно все величины в функциях входного воздействия, начальных и граничных условиях.

2   Постановка краевой задачи

Рассмотрим технический объект, в котором в качестве отдельного элемента можно выделить струну (0<x<2), жестко закрепленную на концах. В начальный момент времени струна смещена в положение согласно рис.3.1 и данное смещение описывается выражением 0,01·sin(πx/l). Натяжение струны T₀ составляет 0,2 Н. Начальной скоростью струна не обладает.

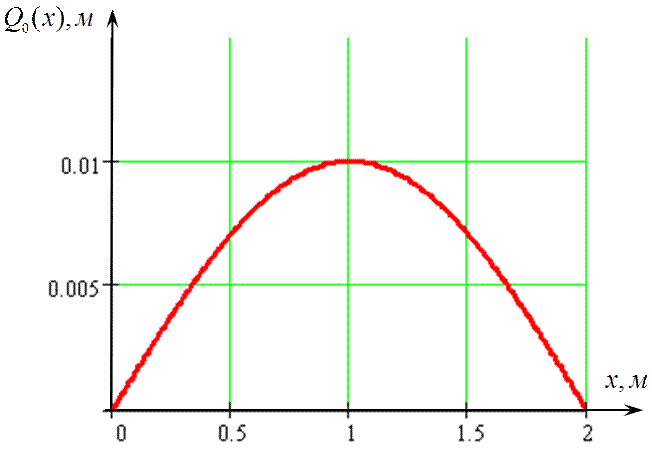
Рис.3.1 – Начальное смешение струны

Колебания струны осуществляется под действием внешней непрерывно распределенной силы с плотностью g(x,t)=0,01·sin(0,1t) Н/м, график которой представлен на рис.3.2.

Материал струны медь, диаметр d=2 мм.

Сформулируем краевую задачу для данного условия.

Функция Q(x,t), описывающая поперечные смещения струны определяется уравнением:

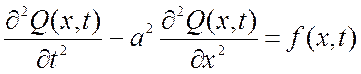.                                                           (3.1)

Данное уравнение одномерное гиперболического типа (содержащее вторые производные по времени t и пространственной координаты х).

Опишем параметры, входящие в данное уравнение.

Волновая скорость струны определяется выражением:

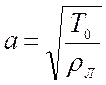 ,                                                                                              (3.2)

где     Т₀ – сила натяжения струны, Н;

          ρ_Л – линейная плотность (масса, приходящаяся на единицу длины струны), кг/м.

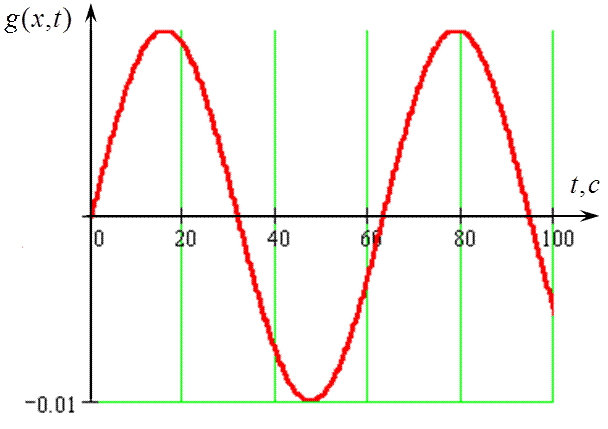
Рис.3.2 – Плотность внешней силы

Рассчитаем линейную плотность струны:

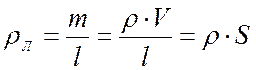,                                                                          (3.3)

где     m – масса струны, кг;

          l – длина струны, м;

          V – объем струны, м³;

          S – площадь поперечного сечения струны, м².

Для струны круглого сечения, площадь:

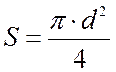                                                                                               (3.4)

или с учетом численных значений:

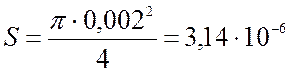           м².

          Плотность меди ρ=8,9·10³ кг/м³ (см. Приложение)

          Тогда линейная плотность струны:

кг/м.

Волновая скорость струны согласно (3.2):

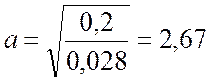м/с.                                                                          

          Входное воздействие (удельная сила) f(x,t), м/с² – это сила, действующая на единицу массы струны, которая через известную линейную плотность внешней силы g(x,t), Н/м определяется через линейную плотность:

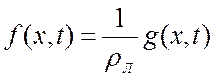.                                                                                (3.5)

С учетом известных значений, имеем:

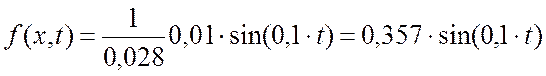.                                (3.6)

Поскольку концы струны закреплены, имеем нулевые граничные условия вида:

;                                                                                  (3.7)

.                                                                                  (3.8)

Начальные условия представляются в виде:

- начальное смещение струны:

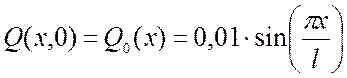;                                                             (3.9)

- начальная скорость струны:

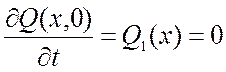.                                                                              (3.10)

Согласно Приложению для выбранного уравнения гиперболического типа стандартизирующая функция имеет вид:

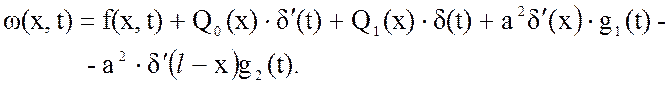                         (3.11)

С учётом входного воздействия (3.6), принятых начальных (3.9),(3.10) и граничных (3.7),(3.8) условий стандартизирующая функция принимает вид:

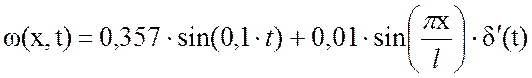.                                (3.12)

Функция Грина (см.Приложение):

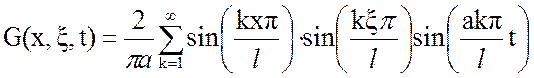.                                                                                                       (3.13)

Передаточная функция (см.Приложение):

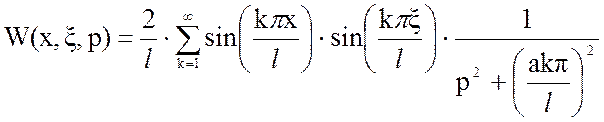.                      (3.14)

3 Расчёт выходной распределенной величины

Идентификация исходного уравнения позволяет перейти к расчету распреде­ленной выходной величины, являющейся функцией как пространственной, так и временной координаты и рассчитываемой как пространственно-временная компози­ция от произведения функции Грина и стандартизирующей функции:

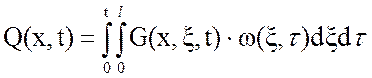.                                                       (3.15)

Выходная распределенная величина Q(x,t) находится как сумма двух составляющих:

Q(x,t)=Q₁(x,t) + Q₂(x,t),                                                                      (3.16)

где     Q₁(x,t) и Q₂(x,t) – первая и вторая составляющие выходной