Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 5

– входной сигнал ω(ξ,τ) распределенный;

– выходной сигнал Q(x^**_k,t) сосредоточенный скалярный (в одной точке x^**₁) или векторный (в нескольких фиксированных m точках x^**_k, k=1,2…m).

Такой блок может использоваться в системах управления, когда формируется сигнал обратной связи датчиком, снимающим показания в одной или нескольких точках. Или когда сосредоточенный выход ξ-блока рассматривается как  интегральная оценка функции состояния, например, ее среднее значение.

Функция состояния подобного блока описывается выражением (1.31), но для фиксированных значений x^**_k:

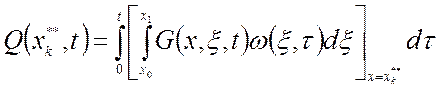.                                                 (1.46)

Передаточная функция переходного ξ-блока находится путем подстановки фиксированных значений x^**_k:

.                                              (1.47)

В терминах передаточных функций ξ-блок выглядит согласно рис.1.5.

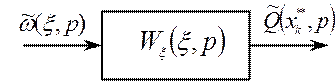
Рис.1.5 – Переходной ξ-блок в терминах передаточных функций

3) Блок, для которого

– входной управляющий сигнал представляет собой пространственной воздействие  φ(ξ) при фиксированном характере изменения входного сигнала во времени υ(τ);

– выходной сигнал Q(x,t) распределенный.

Рассмотрим примеры таких блоков.

а) Начальные и граничные условия нулевые, входное воздействие только по внутреннему пространственном управлению φ(ξ)=f₁(ξ) с фиксированным законом υ(τ)=u(τ), который принимает один из двух вариантов:

– скачкообразное изменение входного сигнала при τ=0:

;                                                                                   (1.48)

– импульсное воздействие на входе блока в фиксированный момент времени τ=t^*:

.                                                                       (1.49)

В этом случае стандартизирующая функция имеет один из следующих видов:

;                                                                                    (1.50)

.                                                                       (1.51)

Тогда согласно (1.31) выходной сигнал соответственно:

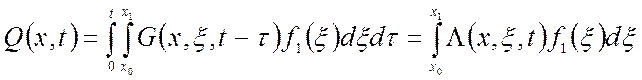 ,                (1.52)

где    Λ(х,ξ,t) – интеграл по времени от функции Грина, который по

аналогии с ССП можно назвать переходной функцией объекта.

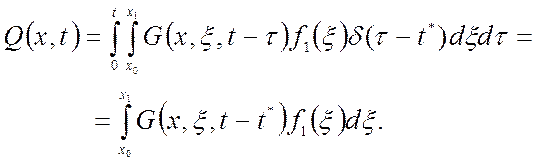                                   (1.53)

В преобразованиях Лапласа выходной сигнал соответственно:

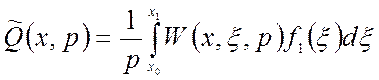;                                                                (1.54)

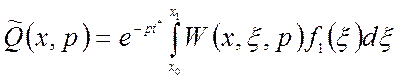.                                                   (1.55)

б) Задача, в которой управляющее воздействие формируется ненулевыми начальными условиями при отсутствии всех прочих воздействий. Например, могут быть следующие варианты записи стандартизирующей функции (1.32):

;                                                                         (1.56)

;                                                                        (1.57)

.                                                                          (1.58)

В выражении (1.58), напомним, Q₁ есть производная функции состояния по времени t.

Выходной сигнал для рассмотренных случаев:

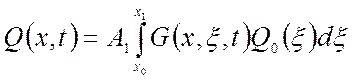          ;                                                         (1.59)

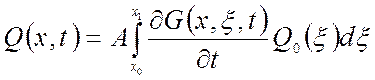;                                                       (1.60)

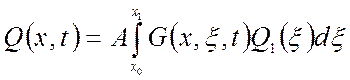.                                                          (1.61)

В преобразованиях Лапласа выходная величина соответственно:

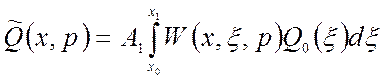;                                                     (1.62)

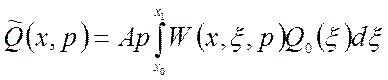;                                                     (1.63)

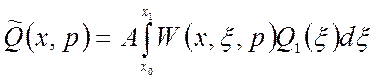.                                                      (1.64)

Для блоков данного типа передаточная функция W(x,ξ,p) никак не упрощается и является функцией трех переменных.

4) Переходной хξ-блок, для которого:

- входной сигнал  ω(ξ,τ)  представляет собой сосредоточенное внешнее воздействие υ(τ) с фиксированным законом φ(ξ)  пространственного распределения;

- выходной сигнал Q(x^**_k,t) сосредоточенный скалярный (в одной точке x^**₁) или векторный (в нескольких фиксированных m точках x^**_k, k=1,2…m).

То есть данный блок обладает свойствами рассмотренных ранее х-блока и ξ-блока.

Передаточная функция хξ-блока рассчитывается из выражения:

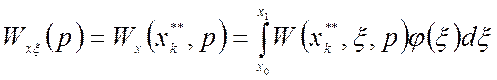.                                     (1.65)

Более подробно о данном типе блока в литературе [15,16].

5) Статический блок, для которого передаточная функция W(x,ξ) не зависит от параметра р. По аналогии с сосредоточенными системами, блок является «безынерционным».

Выходной сигнал статического блока с распределенным входным сигналом будет также являться распределенным:

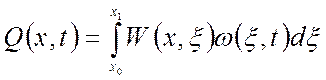.                                                              (1.66)

Функция состояния статического блока с сосредоточенным входным сигналом будет соответственно сосредоточенная и определяться выражением:

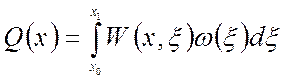.                                                                   (1.67)

Таким образом, рассмотрены все возможные частные случаи блоков с распределенными параметрами.

1.11 Структурное моделирование распределенного блока

Используя рассмотренные частные случаи, осуществим структурное моделирование объекта СРП с выходным распределенным сигналом Q(x,t) для которого стандартизирующая функция представляется в виде суммы, учитывающей входное возмущение, начальные распределения и граничные воздействия по формуле (1.32) с учетом (1.33) и (1.34).

Пусть входное воздействие можно представить в виде:

.                                                                (1.68)

То есть рассматривается частный случай сосредоточенного воздействия υ(τ) с фиксированным законом φ(ξ)  пространственного распределения.

Аналогично представим последние два слагаемых в стандартизирующей функции (1.32), в которые входят граничные условия:

,                                                                        (1.69)

,                                                                        (1.70)

где     φ₀(ξ), φ₁(ξ) согласно (1.33) и (1.34) в зависимости от вида граничных условий определяются выражениями:

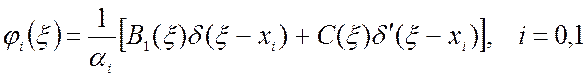                          (1.71)

или

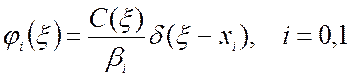.                                                          (1.72)

          С учетом введенных обозначений запишем стандартизирующую функцию в преобразованиях Лапласа: