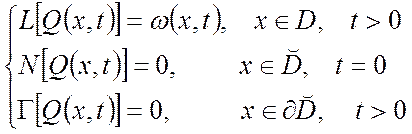(1.25)
Система (1.25) называется стандартной формой базовой задачи (1.1)-(1.3), а функция ω=(x,t) – стандартизирующей функцией.
Используя стандартизирующую функцию, существенно упрощается основное соотношение «вход-выход»:
.
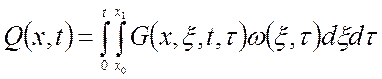(1.26)
Выражение (1.26) называется интегральной формой описания СРП, позволяющее находить решение путем вычисления интеграла по пространственной и временной переменным от произведения функции Грина G(x,ξ,t,τ) и стандартизирующей функции ω(x,t). Необходимо отметить, что при подстановке в интеграл (1.26) стандартизирующей функции, выходные аргументы х, t должны быть заменены на входные переменные ξ, τ.
С учетом введенных понятий линейный распределенный блок в общем виде можно представить согласно рис.1.2.
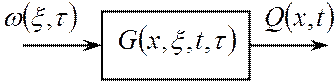
Рис.1.2 – Линейный распределенный блок
Понимать рисунок следует следующим образом. Реакция выходной величины Q(x,t) распределенного блока на входное воздействие ω(ξ,τ) однозначно определяется его функцией Грина G(x,ξ,t,τ).
В дальнейшем будем рассматривать краевую задачу (1.15)-(1.18) в которой коэффициенты А, А1, В1, С, С1, α0, α1, β0, β1 постоянны и В1, С, С1, не зависят от времени:
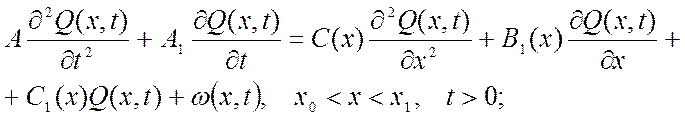(1.27)
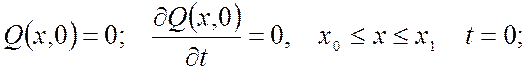(1.28)
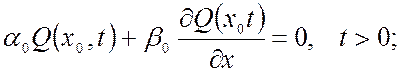(1.29)
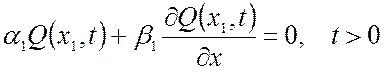. (1.30)
На основании (1.19), аналогично выражению (1.26) решение этой задачи принимает вид:
.
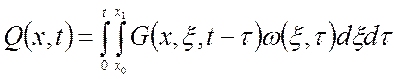(1.31)
Отличие (1.31) от (1.26) заключается в количестве аргументов в функции Грина.
Опуская промежуточные выкладки, на основании интегральных представлениях функции Грина и свойств дельта-функции, стандартизирующая функция ω(ξ,τ) для задачи (1.27)-(1.30) имеет вид:
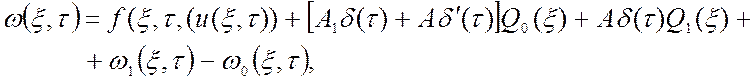(1.32)
где ω0(ξ,τ), ω1(ξ,τ) зависят от вида граничных условий.
В случае первой краевой задачи (β0 =β1=0):
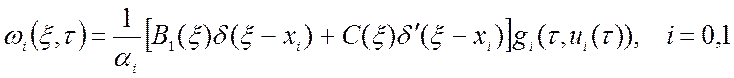. (1.33)
В случае второй и третьей краевой задачи (β0 >0, β1>0):
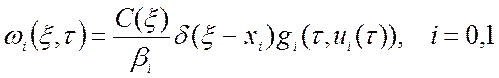. (1.34)
В справочнике Бутковского [6] представлены стандартизирующие функции ω(x,t) для конкретных видов задач, которые самостоятельно могут быть получены на основе выражений (1.32)-(1.34).
Применяя преобразование Лапласа по временному аргументу t к выражению (1.31), получим:
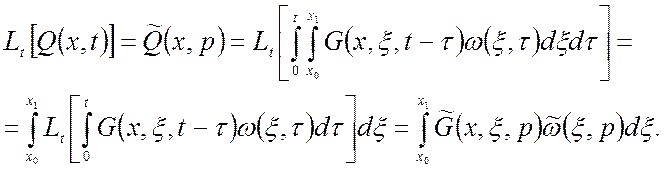(1.35)
Операцию пространственной композиции, представляющей собой интеграл по пространственной переменной, обозначим в виде:
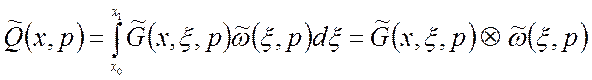. (1.36)
Согласно ТАУ для линейных сосредоточенных систем справедливо соотношение:
.
(1.37)
По аналогии изображение Лапласа от функции Грина называется передаточной функцией объекта с распределенными параметрами:
.
(1.38)
Тогда распределенный блок, используя структурный подход, также можно представить согласно рис.1.3.
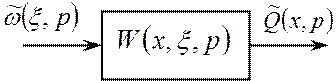
Рис.1.3 – Распределенный блок в терминах передаточных функций
В справочнике Бутковского [6] представлены передаточные функции W(x,ξ,p) для конкретных видов задач, которые самостоятельно могут быть получены путем применения преобразования Лапласа к известной функции Грина.
1.10 Типовые распределенные блоки
На практике в зависимости от вида входных и выходных сигналов распределенного блока выделяют ряд частных случаев. Для их описания стандартизирующую функцию (входной сигнал) представим в виде:
,
(1.39)
где φ(ξ) – пространственное воздействие;
υ(τ) – сосредоточенное воздействие.
Рассмотрим типовые распределенные блоки.
1) Переходной х-блок, для которого:
– выходной сигнал Q(x,t) распределенный;
– входной сигнал ω(ξ,τ) представляет собой сосредоточенное внешнее воздействие υ(τ) с фиксированным законом φ(ξ) пространственного распределения.
Такой блок может использоваться, например, в системах управления, когда управляющее воздействие с регулятора на распределенный объект подается в фиксированную точку его пространственной области. Рассмотрим возможные частные случаи переходного х-блока.
а) Начальные и граничные условия нулевые, входное воздействие только по сосредоточенному внутреннему управлению υ(τ)=u(τ) с фиксированным законом φ(ξ)=f1(ξ). В этом случае стандартизирующая функция:
.
Тогда согласно (1.31) выходной распределенный сигнал:
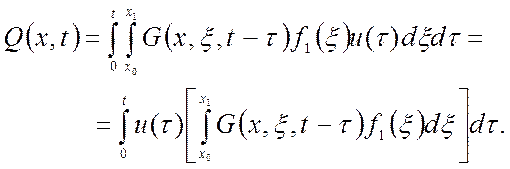(1.40)
В преобразованиях Лапласа (1.40):
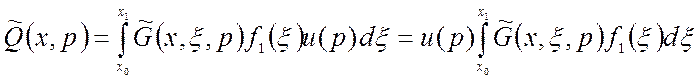. (1.41)
Тогда передаточная функция х-блока принимает вид:
.
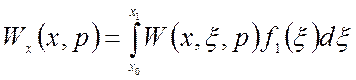(1.42)
В терминах передаточных функций х-блок выглядит согласно рис.1.4.
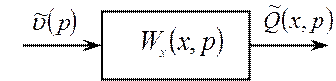
Рис.1.4 – Переходной х-блок в терминах передаточных функций
б) Распределенный блок с граничным управлением υ(τ)=ui(τ), сосредоточенным в точке х=хi на одной из границ области [х0,х1] определения пространственной переменной, при отсутствии всех других входных воздействий. В этом случае стандартизирующая функция принимает вид (1.33) или (1.34) в зависимости от вида граничных условий, при чем только для i=0 или i=1.
Тогда согласно (1.31) выходной сигнал данного блока с учетом свойств дельта-функции:
– для второй и третьей краевой задачи:
;
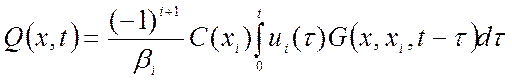(1.43)
– для первой краевой задачи:
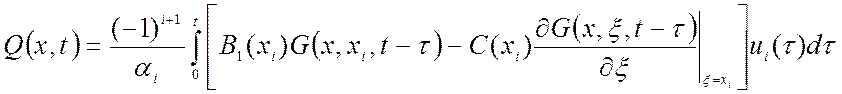В
последнем выражении сначала находится производная от функции Грина по
пространственной переменной ξ, а затем вместо переменной ξ подставляется
значение хi.
Передаточные функции для переходных х-блоков с граничным сосредоточенным управлением имеют вид:
– для второй и третьей краевой задачи:
;
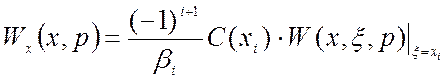(1.44)
– для первой краевой задачи:
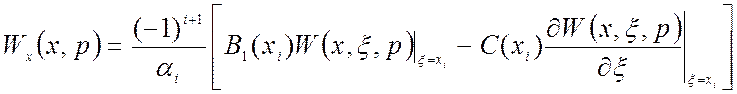. (1.45)
Как видно из (1.42), (1.44), (1.45) передаточная функция х-блока зависит от двух переменных: выходной пространственной переменной х и оператора Лапласа р.
2) Переходной ξ-блок, для которого:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.