Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 7

Поскольку концы струны закреплены, граничные условия нулевые:

; .                                                              Начальные условия по условию задачи также равны нулю:

;        

.      

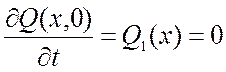Пример 3.

Сформулировать краевую задачу о вынужденных поперечных колебаниях струны, закрепленной на одном конце (х=0) и подверженной на другом конце (x=l) действию возмущающей силы, которая вызывает смещение, равное А·sin(ωt), где ω≠(kπa/t) (k=1,2…). В момент времени t=0 смещения и скорости равны нулю.

Функция Q(x,t), описывающая вынужденные колебания струны определяется уравнением:

.

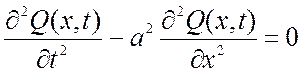Начальные условия:

;        

.      

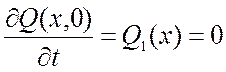Граничные условия задаются в виде:

;

.         

2.2 Уравнения продольных колебаний стержня

Рассмотрим стержень длиной l, который в положении равновесия находится вдоль оси Ох. Его продольные колебания описываются функцией Q(x,t), представляющей собой в каждый момент времени t продольное смещение точки стержня, координата которой в положении равновесия была равна х. Предполагается, что натяжение в стержне подчиняется закону Гука. Тогда уравнение, описывающее продольное колебание стержня имеет вид:

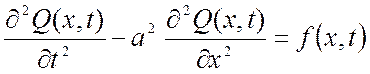,                                                       (2.15)

где     а – волновая скорость, м/с;

          f(x,t) – удельная сила, м/с².

          Волновая скорость стержня определяется согласно выражению:

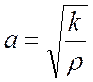,                                                                                               (2.16)

где     k – коэффициент упругости, Н;

          ρ – линейная плотность (масса, приходящаяся на единицу длины стержня), кг/м.

          Коэффициент упругости k может быть найден следующим образом:

          ,                                                                                              (2.17)

где     S – площадь поперечного сечения стержня, м²;

          Е – модуль Юнга (напряжение, возникающее в образце при увеличении (уменьшении) его длины в два раза при прочих неизменных условиях), Н/м².

          Для однородного стержня k=const, ρ=const. В противном случае k(х), ρ(х).

Удельная сила, в свою очередь, может быть представлена в виде:

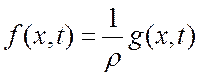,                                                                                (2.18)

где     g(x,t) – линейная плотность продольной внешней силы (сила, действующая на единицу длины), Н/м.

Начальные условия задаются в виде:

– профиля начальных смещений:

;                                                                         (2.19)

– профиля начальной скорости:

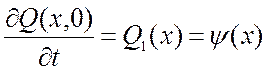.                                                                      (2.20)

Граничные условия могут быть заданы для следующих случаев:

1) Первая краевая задача (граничные условия 1 рода):

;                                                                          (2.21)

,                                                                          (2.22)

где     μ₁(t), μ₂(t) – заданные функции времени, описывающие закон

движения конца стержня.

Для жестко закрепленного конца μ(t)=0.

          2) Вторая краевая задача (граничные условия 2 рода):

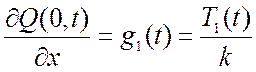;                                                                        (2.23)

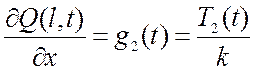,                                                                        (2.24)

где     T₁, T₂ – сила натяжения, приложенная к концу стержня, Н.

          В случае свободного конца, натяжение стержня вблизи него отсутствует (g(t)=0).

3) Третья краевая задача (граничные условия 3 рода):

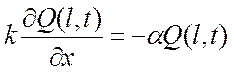.                                                                           (2.25)

Данные условия формулируются в случае упругого закрепления стержня, при котором конец стержня может перемещаться, но возникает упругая сила, стремящаяся вернуть сместившийся конец в прежнее положение.

Пример.

Сформулировать краевую задачу о продольных колебаниях однородного цилиндрического стержня, один конец которого заделан, а к другому концу приложена сила F(t)=A·sin(ωt), направление которой совпадает с осью стержня.

Функция Q(x,t), описывающая продольные колебания стержня определяется уравнением:

.

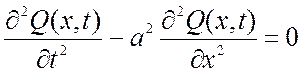Начальные условия нулевые:

;        

.      

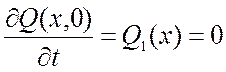Граничные условия задаются в виде:

;

,

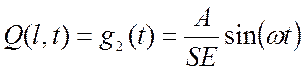где     S – площадь поперечного сечения стержня, м²;

          E – модуль Юнга материала стержня, Па (см. Приложение).      

Общие замечания.

1) Если рассматривается колебательный процесс струны (стержня), у которой концы находятся достаточно далеко и в течение небольшого интервала времени влияние концов еще не успевает проявиться, то можно считать струну бесконечной. При этом рассматривается задача, в которой  -∞<x<∞ и граничные условия не формулируются.

2) Если рассматриваемый участок струны (стержня) находится вблизи от одного его конца и далеко от другого, то рассматривается задача о полубесконечной струне, когда 0≤x<+∞ и граничные условия формулируются только на одном ее конце.

2.3 Уравнения крутильных колебаний стержня

Рассмотрим круговой цилиндрический стержень длиной l, который под влиянием некоторой причины совершает крутильные колебания. Под крутильными колебаниями будем понимать такие колебания, когда поперечные сечения стержня остаются плоскими и поворачиваются одно относительно другого без искажений, вращаясь вокруг оси стрежня.

Тогда уравнение, описывающее крутильное колебание стержня имеет вид:

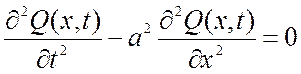,                                                                (2.26)

где     а  – скорость, м/с, определяемая из выражения:

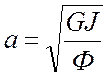,                                                                                             (2.27)

где     G – модуль сдвига (описывает отклик материала на сдвиговую нагрузку), Па;

          J – полярный момент инерции поперечного сечения, кг·м²;

          Ф – осевой момент инерции стержня, приведенный к длине, кг·м.

          Модуль сдвига связан с модулем Юнга Е через коэффициент Пуассона υ:

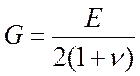.                                                                                       (2.28)

Значения модуля сдвига G для ряда материалов при комнатной температуре представлены в табл.2.1.