Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 12

                                                   величины, определяемые согласно выражениям:

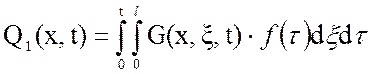                                                        (3.17)

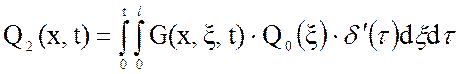                                            (3.18)

Рассчитаем отдельно каждую составляющую решения.

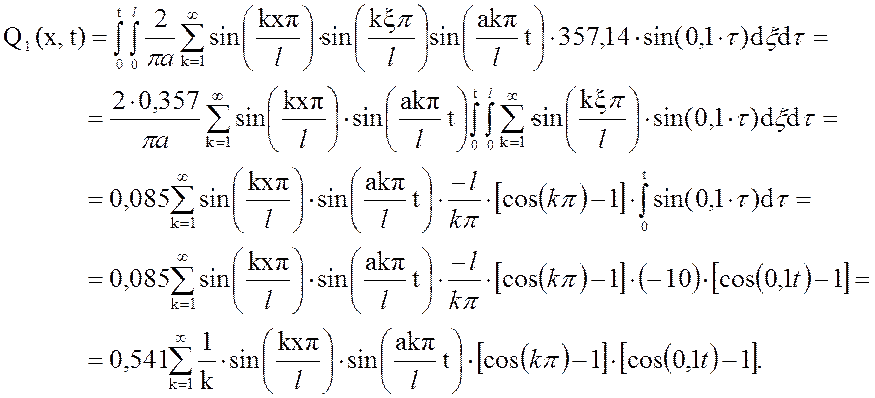Первая составляющая решения выходной функции:

           Вторая составляющая решения выходной функции:

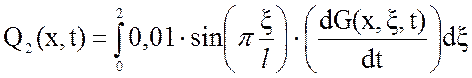.                                          (3.19)

Первоначально определим производную по времени t от функции Грина:

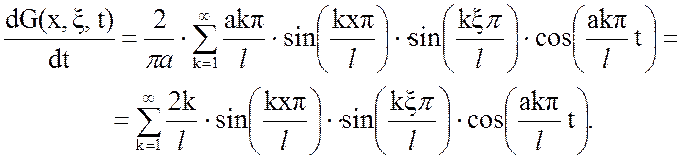            (3.20)

Подставим уравнение (3.20) в (3.19):

             

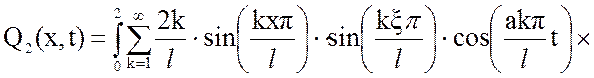
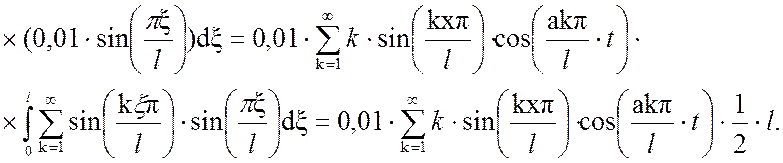
Выходная величина, в результате суммирования двух составляющих решения:

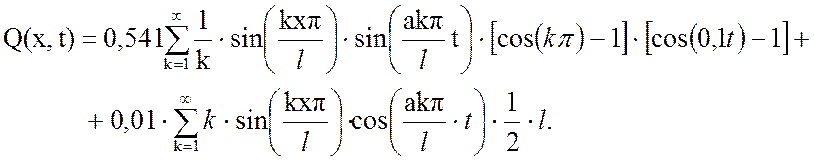   (3.21)

Как видно из выражения (3.21) она является функцией двух аргументов: пространственной координаты х и временной координаты t. Построим график этой функции при фиксированном времени t при помощи программы MathCAD. На рис.3.3. и 3.4 – плоские графики, при чем на первом графике при t=2с струны выпуклая, а на втором - t=4с она вогнутая.

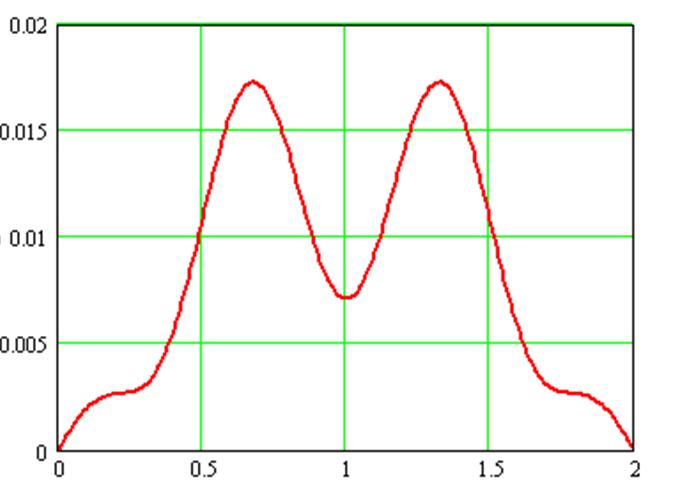
Рис.3.3 – График выходной величины Q(x,t) при t=2с

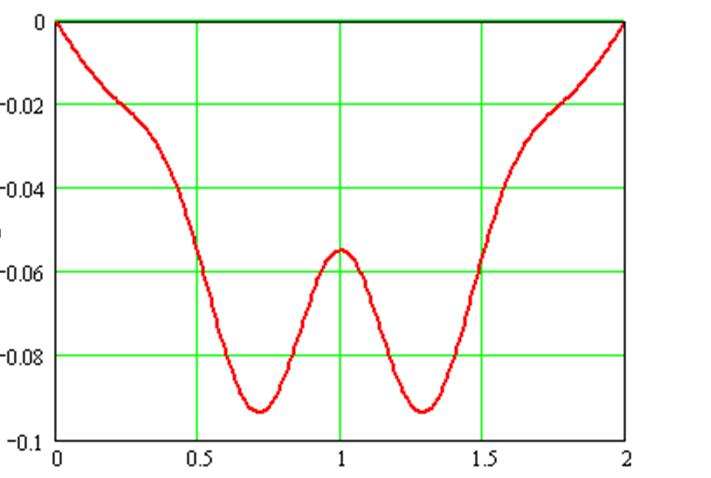
Рис.3.4 – График выходной величины Q(x,t) при t=4с

На рис.3.5 представлен объемный график, позволяющий видеть, как нарастают колебания струны во времени.

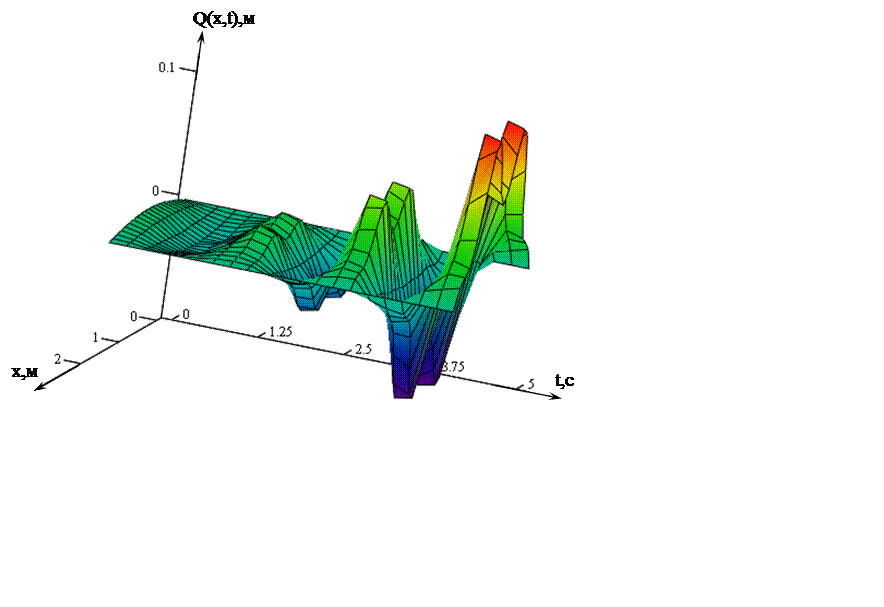
Рис.3.5 – Зависимость выходной величины от времени t и координаты х

4 Оценка динамических свойств объекта моделирования

Для рассматриваемой струны стандартизирующая функция представляется в виде суммы, учитывающей входное возмущение и начальное распределения (3.12) или в общем виде:

,                                                     (3.22)

где     ;

          ;

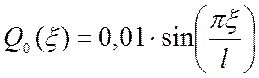          ; А=1.

          Преобразуем по Лапласу (см.Приложение) слагаемые:

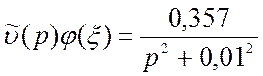;                                                                      (3.23)

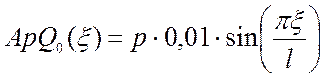.                                                             (3.24)

Тогда стандартизирующая функция в преобразованиях Лапласа:

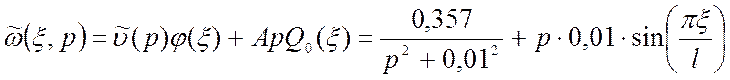          .    (3.25)

При структурном представлении распределенный объект (струна) с передаточной функцией W(x,ξ,p), входное воздействие которого описывается выражением (3.25), можно представить в виде рис.3.6.

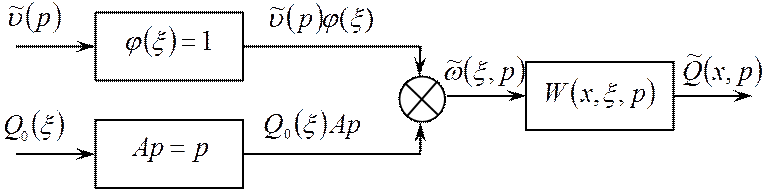
Рис.3.6 – Структурное представление струны

Перенесем сумматор через звено с передаточной функцией W(x,ξ,p) (рис.3.7).

Выходную распределенную величину тогда можно найти следующим образом:

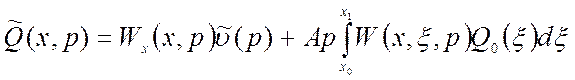.                          (3.26)

Так как φ(ξ)=1, то передаточная функция х-блока может быть найдена как интеграл по переменной ξ от заданной передаточной функции:

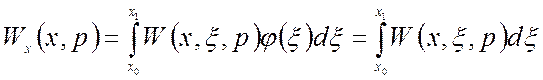                                        (3.27)

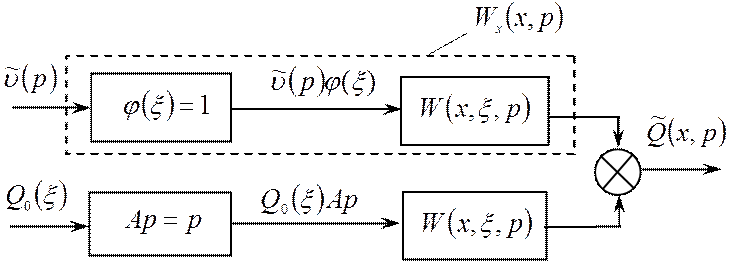
Рис.3.7 – Преобразование структурного представления струны

Выполним данное преобразование:

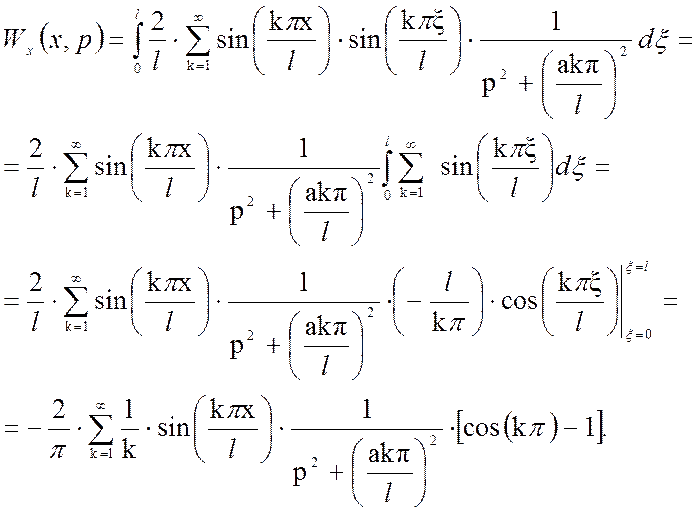                  (3.28)

Рассчитаем второе слагаемое:

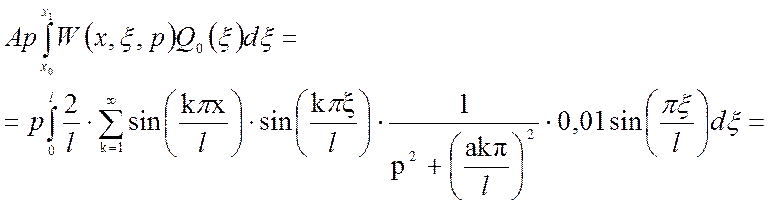
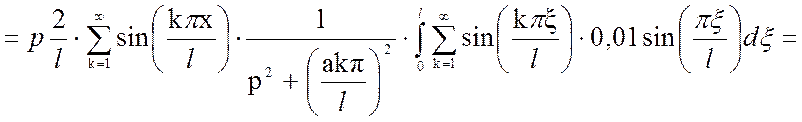
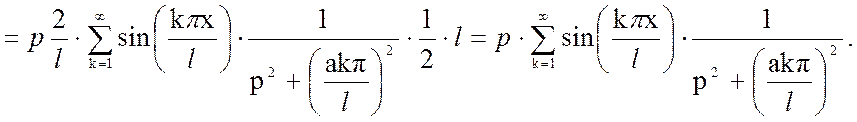          Выходная величина с учетом (3.26), (3.28) и последнего выражения:

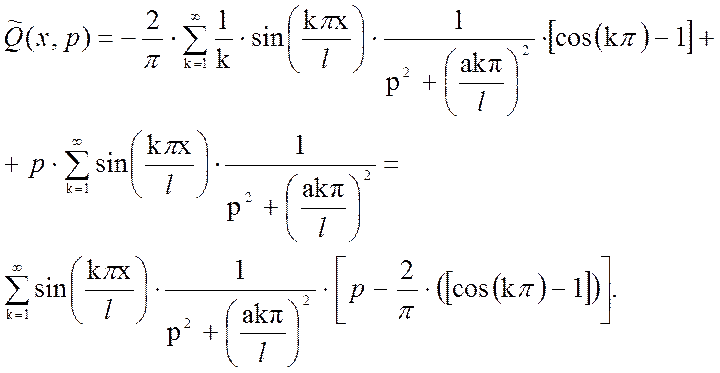          Предположим, что начальное отклонение струны равно 0. При этом в качестве единственного входного (управляющего) воздействия рассматривается . Тогда выходная распределенная величина:

.                                                                   (3.29)

Построим логарифмическую амплитудно-частотную характеристику (ЛАЧХ) для точки х=l/2. С этой целью запишем частотную передаточную функцию в этой точке:

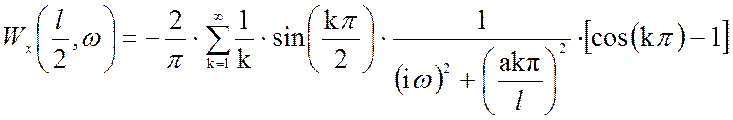.   (3.30)

Тогда ЛАЧХ, построенная с использованием программы MathCAD представлена на рис.3.8.

В первом приближении построенную ЛАЧХ можно аппроксимировать стандартными типовыми наклонами 0 и -40 дб/дек и записать упрощенную передаточную функцию в виде апериодического звена второго порядка:

,                                                                             (3.31)

где     k,T₁ – коэффициент преобразования и постоянная времени соответственно.

          Их величины определяются из рис.3.8:

          ,

          ;

          .

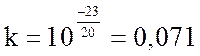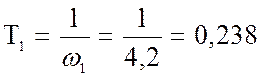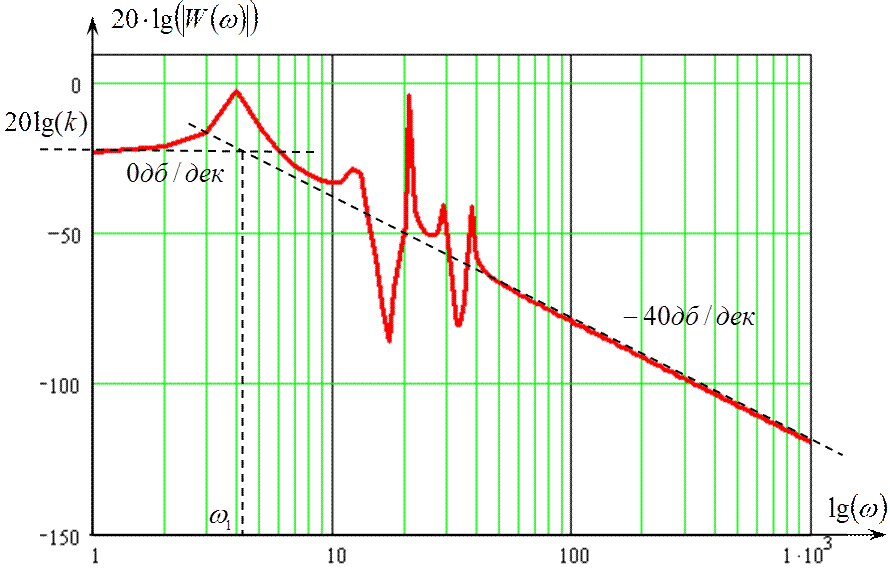
Рис.3.8 – Логарифмическая амплитудно-частотная характеристика

          Тогда аппроксимированная передаточная функция принимает вид:

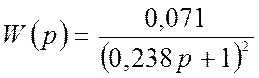.                                                                       (3.32)

Данная передаточная функция получена для центра струны и позволяет применять методы исследования согласно теории автоматического управления как для системы с сосредоточенными параметрами.

ВАРИАНТЫ ЗАДАНИЙ

Варианты заданий выбираются по группам согласно номеру в журнале. Например, пятый студент из второй группы – вариант 2.5, десятый студент из первой группы – вариант 1.4.

Вариант 1.1

Сформулировать и решить краевую задачу о вынужденных колебаниях кольцевой мембраны, упруго закрепленной на внешнем и внутреннем радиусах под действием внешней плотности силы g(r,t)=A·sin(B·t). Начальные условия принять нулевыми.

Вариант 1.2

Поставить и решить краевую задачу определения температурного поля диска радиусом R, который в начальный момент времени нагрет равномерно до температуры Θ. На радиусе R температура диска поддерживается неизменной и равной Θ. Внешнее воздействие на диск описывается синусоидальным законом А·sin(D·t).

1	;     ;   a ≠ 0
2
3
4
5	, μk – положительные корни уравнения:
6

Вариант 1.3

Поставить и решить краевую задачу определения температурного поля диска радиусом R. В начальный момент времени температурное поле диска подчиняется закону F(r). На радиусе R температура диска изменяется по синусоидальному закону Θ·sin(D·t). Внешнее воздействие на диск отсутствует.

1	;     ;   a ≠ 0
2
3	,
4
5
6

Вариант 1.4

Круглая однородная мембрана радиуса R, закрепленная по контуру, в начальный момент времени выпуклая (вид задать самостоятельно). В момент времени t=0 к поверхности мембраны приложена равномерно распределенная гармоническая сила плотностью g(r,t)=Asin(ωt). Сформулировать  и решить краевую задачу при данных условиях. Начальную скорость принять равной нулевой.

1	;     ;   a > 0
2	,
3	,
4
5	, μn – положительные корни уравнения:
6

Вариант 1.5