Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 2

   , x  ∂Ď,   t>0,                                                                                                                   (1.3)

где     ∂Ď – граница области Ď;

– линейный оператор;

g(x,t) – внешнее воздействие, которое можно рассматривать как

             второй вход объекта.

Уравнения (1.1)-(1.3) с заданными операторами L,N,Г составляют базовую модель для математического описания объекта СРП или краевую задачу.

В зависимости от вида оператора L существует разделение на классы уравнений. Рассмотрим здесь и далее на примере одномерной задачи, когда пространственная распределенность Q(x,t) зависит от одной координаты х. В этом случае уравнение (1.1) можно расписать в виде:

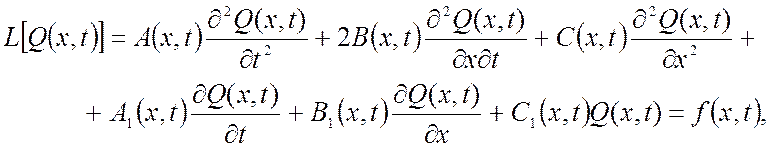 (1.4)

где     А,В,С,А₁,В₁,С₁ – заданные функции или константы.

В зависимости от дискриминанта Δ=АС-В² различают следующие классы уравнений:

а) Δ <0 – уравнения гиперболического типа;

б) Δ =0 – уравнения параболического типа;

в) Δ >0 – уравнение эллиптического типа;

г) Δ меняет знак в области допустимых изменений х и t – смешанная

  задача.

Далее рассмотрим примеры уравнений разных классов.

1.2 Уравнения гиперболического типа

Содержат вторые производные, как по времени t, так и по координате x. Описывают колебательные процессы различной природы (механические, электромагнитные, звуковые и т.д.), связанные с конечной скоростью ν распределения волновых явлений.

Например, если в уравнении (1.4) принять условия:

В=А₁=В₁=С₁=0;

f(x,t)=0;

А=1;

С=- ν²;

Δ <0, то уравнение приобретает вид:

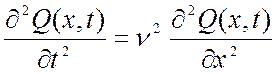,                                                                                                                                    (1.5)

где     ν²=const>0, .                                       

Уравнение (1.5) называется волновым уравнением, которое моделирует процессы распространения свободных колебаний и является одним из уравнений математической физики.

Если внешнее воздействие отлично от нуля f(x,t) ≠0, то уравнение (1.5) описывает вынужденные колебания под влиянием внешнего воздействия:

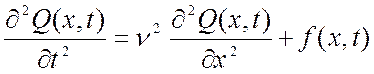, .                       (1.6)

Если к рассмотренному уравнению добавить условия А₁>0, С₁>0, то получим уравнение вида:

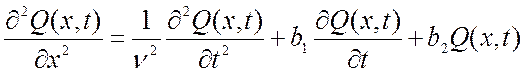,                                   (1.7)

где     b₁,b₂=const>0, .                                   

Уравнение (1.7) называется телеграфным уравнением гиперболического типа, а ν является скоростью распространения электромагнитной волны вдоль линии. Данное уравнение описывает распределение напряжения и тока вдоль длинной электрической линии.

При b₁,b₂=0 уравнение (1.7) сводится к волновому уравнению, а при b₂=0, b₁>0 моделирует процессы механических колебаний в сопротивляющейся среде.

1.3 Уравнения параболического типа

Содержат первую производную по времени t и вторую производную по x. Описывают задачи, связанные с процессами теплопроводности, диффузии, движения вязкой жидкости и т.д.

Например, если в уравнении (1.4) принять условия:

А=В=В₁=С₁=0;

f(x,t)=0;

А₁=1;

С= - а<0;

Δ =0, то уравнение приобретает вид:

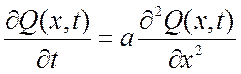, ,                                                                                                         (1.8)

где     a=const>0, .                                         

Уравнение (1.8) называют уравнением теплопроводности (уравнением Фурье).  Описывает температурные поля процессов теплопроводности, тепломассопереноса, электромагнитного поля и т.д.

Также это уравнение может быть неоднородным, учитывающим внешнее воздействие f(x,t) от внутренних источников вещества и энергии:

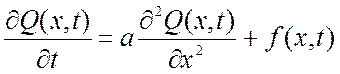.                                                                                                                           (1.9)

1.4 Уравнения эллиптического типа

Отсутствует производная по времени t. Описывают статическое состояние объекта СРП. Некоторые из них представлены в табл.1.1.

Табл. 1.1

Уравнение Гельмгольца	Уравнение Пуассона	Уравнение Лапласа
, .	, .	, .

Уравнение Гельмгольца описывает многие физические процессы теплопроводности, диффузии в движущихся средах, напряженности магнитного поля, установившиеся колебания различной природы.

Уравнения Пуассона и Лапласа моделируют распределение температурного потенциала, скоростей при стационарном течении несжимаемой жидкости, потенциала электрического поля в задачах электростатики и т.д. при отсутствии или наличии внешних воздействий соответственно.

1.5 Начальные условия в краевой задаче 

Как указывалось ранее, для получения однозначного решения необходимо в постановке краевой задачи указать начальные условия – начальную функцию Q₀(x). Данная функция должна описывать начальные (при ) распределения во всей замкнутой области Ď самой функции состояния Q(x,t) и m-1 ее производных по времени t, где m - порядок старшей производной ∂^mQ/∂t^m в уравнении (1.1). Так как порядок старшей производной меняется в зависимости от класса уравнений, то рассмотрим их в отдельности.

Для гиперболических уравнений (m=2) должна быть задана сама функция и ее первая производная:

;

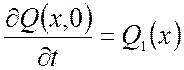.                                                                                (1.10)

Для параболических уравнений (m=1) задается только сама функция в начальный момент времени:

.                                                                                    (1.11)

Для эллиптических уравнений начальные условия отсутствует, т.к. описывают статические состояния СРП и не зависят от t.

1.6 Граничные условия в краевой задаче 

Так как особенностью СРП является необходимость использования граничных условий, рассмотрим их основные типы.

При исследовании процессов в неограниченном пространстве (идеализированные задачи о бесконечных струнах, стержнях и т.д.) граничные условия отсутствуют.

При ограниченном объеме области Ď линейный оператор Г в уравнении (1.3) может иметь один из следующих видов:

1) Первая краевая задача (задача Дирихле, граничные условия первого рода):

 , х ∂Ď, t>0.                                                        (1.12)