Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 13

Сформулировать и решить краевую задачу о вынужденных колебаниях круглой трубы, длиной lс нулевыми начальными условиями, если на концах струны труба закреплена неподвижно, а с внутренней и внешней поверхности труба испытывает со стороны заделки сопротивление, пропорциональное отклонению и направленное противоположно ему. Внешнее воздействие на трубу описывается плотностью силы g(r,z,t)=A·sin(B·t).

1	;     ;    ;   a > 0
2	Q(r,z,0) = Q0(r,z);
3	;        ; ;
4
5
	где λn –положительные корни уравнения:
6

Вариант 1.6

Сформулировать и решить краевую задачу о вынужденных колебаниях прямоугольной мембраны (0≤х≤l₁, 0≤y≤l₂), если в начальный момент времени t=0 отклонение точек мембраны от плоскости xOy и ее скорость равны нулю. Мембрана закреплена неподвижно на плоскостях (0,у) и (l₁,y) и свободна на других плоскостях. Внешнее воздействие на мембрану описывается плотностью силы g(x,y,t)=A·sin(B·t).

1	;     ;    ;   a > 0
2	Q(x,y,0) = Q0(x,y);
3	Q(0,y,t) = g1 (у,t);          Q(l1,y,t) = g2 (y,t); ;         ;
4
5	; ;   ;
6

Вариант 1.7

Сформулировать и решить краевую задачу о вынужденных колебаниях прямоугольной мембраны (0≤х≤l₁, 0≤y≤l₂), если в начальный момент времени t=0 отклонение точек мембраны от плоскости xOy и ее скорость равны нулю. Мембрана закреплена неподвижно на плоскостях (0,у) и (х,0) и свободна на других плоскостях. Внешнее воздействие на мембрану описывается плотностью силы g(x,y,t)=A·sin(B·t).

1	;     ;    ;   a > 0
2	Q(x,y,0) = Q0(x,y);
3	Q(0,y,t) = g1 (у,t);          ;         ;
4
5	;;;
6

Вариант 1.8

Сформулировать и решить краевую задачу о колебаниях однородной струны (0<x<l), закрепленной на одном конце и свободной на другом, под действием внешней непрерывно распределенной силы с плотностью g(x,t)=Asin(ωt), где ω≠(kπa/t) (k=1,2…). Начальные условия нулевые.

1	, ,  a ≠ 0
2	,
3	,
4
5
6

Вариант 1.9

Для тонкого однородного стержня длиной l, начальная температура которого Q₀(x), поставить краевую задачу об определении его температуры. При этом один его конце х=0 и боковая поверхность теплоизолированы, а на другом его конце х= l происходит конвективный теплообмен по закону Ньютона с окружающей средой, температура которой изменяется по синусоидальному закону.

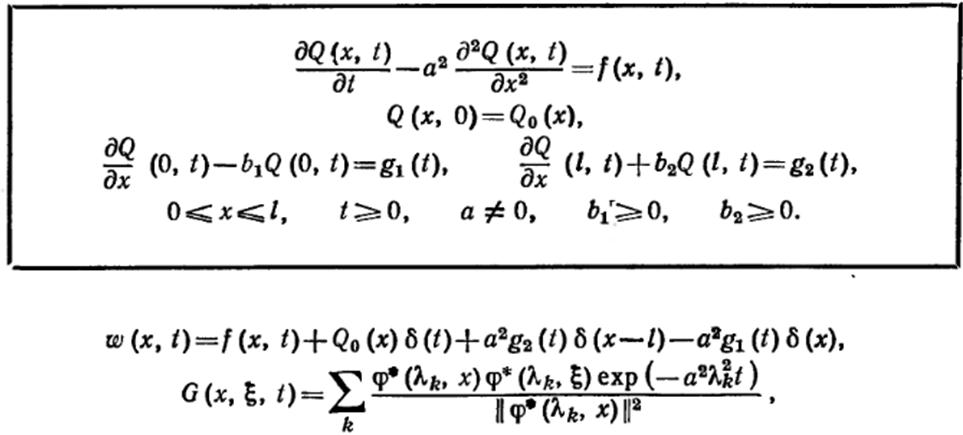
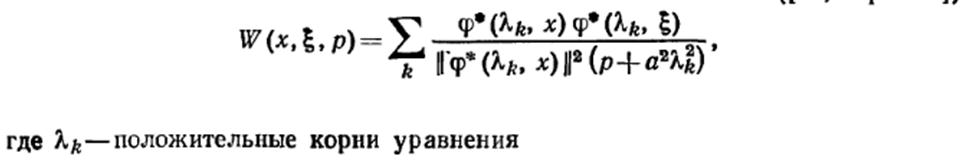
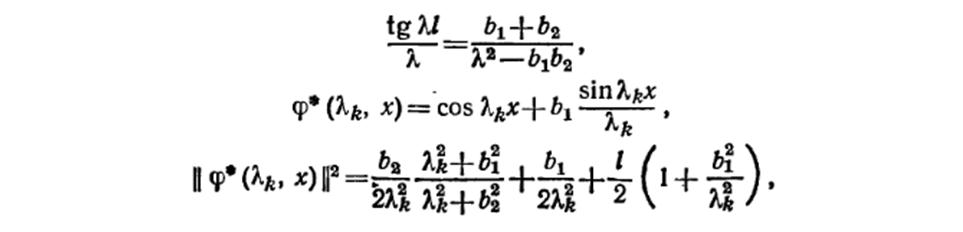
Вариант 1.10

Найти силу тока I(x,t) в проводе длиной l, по которому течет переменный ток, если утечка тока отсутствует, а омическим сопротивлением и проводимостью можно пренебречь. Предполагается, что начальный ток в проводе (при t=0) равен нулю, а начальное напряжение задается формулой:

.

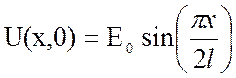Левый конец провода (х=0) заземлен, а правый конец (х=l) изолирован.

1	, ,  a ≠ 0
2	,
3	,
4
5
6

Вариант 1.11

Линия передачи длиной 1000 км находится изначально в установившемся режиме с потенциалом 1200 В на передающем конце (х=0) и 1100 В на приемном конце (х=l=1000). Приемный конец линии внезапно заземляется, а на источнике сохраняется потенциал 1200 В. Сформулировать краевую задачу для потенциала  в линии передач, предполагая индуктивность и проводимость изоляции пренебрежимо малыми.

1	;     ;   a ≠ 0
2
3
4
5
6

Вариант 1.12

Для тонкого однородного стержня длиной l, начальная температура которого Q₀(x), поставить краевую задачу об определении его температуры. При этом, температура на одном его конце х=0 поддерживается постоянной u₀, а на другом его конце х= l происходит конвективный теплообмен по закону Ньютона с окружающей средой, температура которой изменяется по синусоидальному закону.

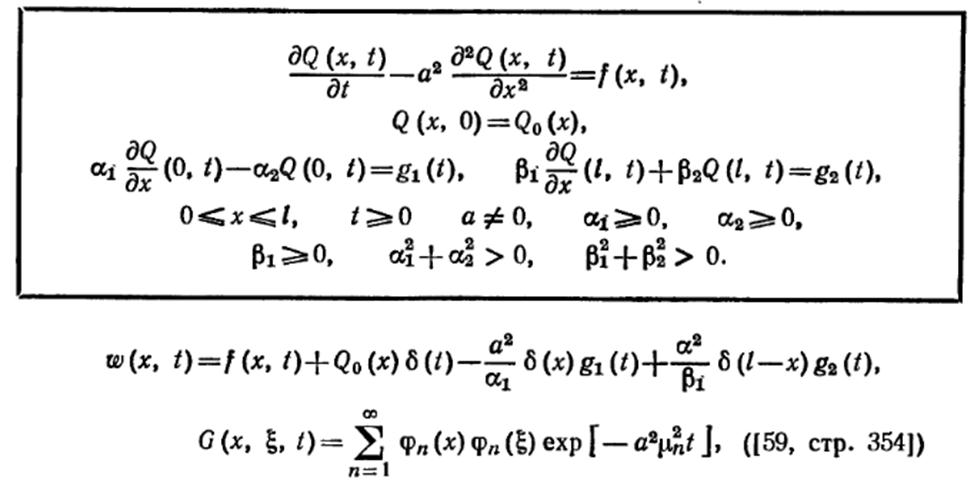
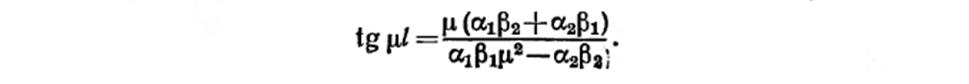
Вариант 1.13

Для тонкого однородного стержня длиной l, начальная температура которого Q₀(x), поставить краевую задачу об определении его температуры. При этом, температура на одном его конце х=0 поддерживается постоянной u₀, а на другом его конце х= l и на боковой поверхности происходит конвективный теплообмен по закону Ньютона с окружающей средой нулевой температуры.

Входное воздействие, описывающее конвективный теплообмен на боковой поверхности задать выражением:

,

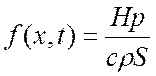где     H – коэффициент теплообмена, Вт/(К·м²);

p – периметр поперечного сечения стержня, м;

S – площадь поперечного сечения стержня, м²;

c – удельная теплоемкость вещества, Дж/(кг·К);

          ρ – плотность материала стержня, кг/м³.

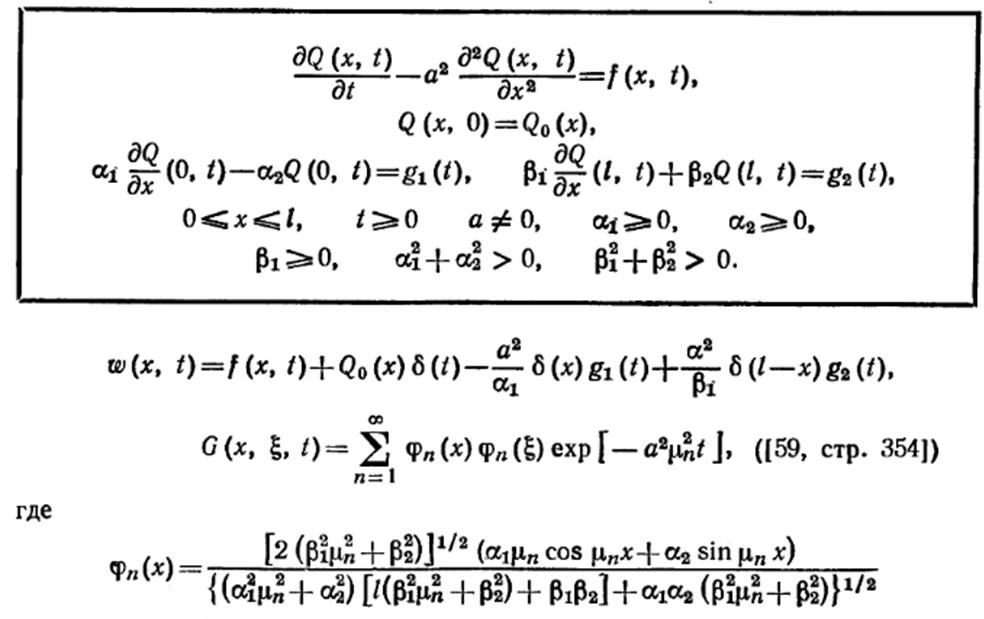
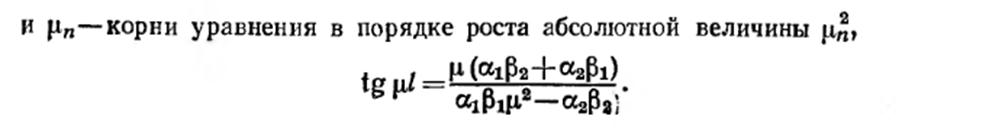Вариант 1.14

Поставить и решить краевую задачу определения температурного поля одномерного однослойного шара радиусом R. В начальный момент времени температурное поле подчиняется закону F(r). Шар помещен в среду с температурой Θ, при этом теплообмен на поверхности подчиняется закону Ньютона и коэффициент теплоотдачи (теплообмена) равен Н. Коэффициент теплопроводности шара k.

1	;     ;   a ≠ 0;
2
3
4
5	, μk – расположенные в порядке возрастания положительные корни уравнения:
6

Вариант 1.15

Пусть стержень длиной lпогружают в пар до тех пор, пока температура во всех его точках не достигнет 100⁰С. В момент времени t=0 его боковую поверхность теплоизолируют, а его оба конца вставляют в лед при 0⁰С. Сформулировать и решить краевую задачу для вычисления температуры стержня после выполнения сформулированных условий.

1	;     ;   a ≠ 0
2
3
4
5
6

Вариант 1.16