Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 9

Функция Q(r,t), описывающая колебания круглой мембраны определяется уравнением:

,

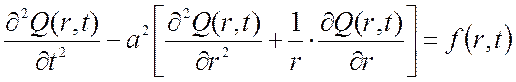где     .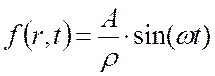

Начальные и граничные условия при этом:

 ;           ;     .

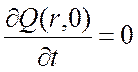2.5 Уравнение распределения температуры в стержне

Рассмотрим тонкий стержень, в пределах любого сечения которого температуру будем считать постоянной, окруженный теплоизолирующей оболочкой. Направим ось Ох вдоль данного стержня. Температура стержня в каждой его точке х в момент времени t описывается функцией Q(x,t) согласно уравнению:

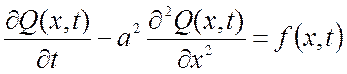,                                                                     (2.48)

где     а² – коэффициент температуропроводности, м²/с;

          f(x,t) – внешнее воздействие, К/с.

Коэффициент температуропроводности рассчитывается из выражения:

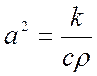,                                                                                              (2.49)

где     k – коэффициент теплопроводности вещества, Вт/(м·К);

          c – удельная теплоемкость вещества, Дж/(кг·К);

          ρ – плотность вещества, кг/м³.

          Внешнее воздействие определяется следующим образом:

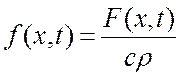,                                                                                  (2.50)

где     F(x,t) – функция плотности тепловых источников, которая определяет количество теплоты, выделяющееся за единицу времени в единице объема тепла

Некоторые значения коэффициента температуропроводности представлены в табл.2.2 [23, с.838].

Табл.2.2

№	Материал	а2, м2/с
1	Серебро	1,7·10-4
2	Медь	1,15·10-4
3	Алюминий	0,85·10-4
4	Железо	0,15·10-4
5	Бетон	0,005·10-4

Начальные условия для уравнения теплопроводности состоят в задании температуры всех точек стержня в начальный момент времени:

.                                                                         (2.51)

Для задания граничных (краевых условий) могут быть использованы следующие варианты [11]:

1) Температура на конце стержня поддерживается по определенному закону (граничные условия 1 рода):

;                                                                          (2.52)

.                                                                          (2.53)

2) На конце стержня (например, при х=0) задан тепловой поток q(t) (граничные условия 2 рода):

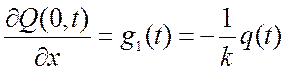,                                                                   (2.54)

где     k – коэффициент теплопроводности вещества, Вт/(м·К).

          В частности в случае теплоизолированного конца тепловой поток через него отсутствует:

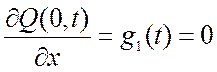.                                                                             (2.55)

3) На конце стержня происходит теплообмен с окружающей средой по закону Ньютона (граничные условия 3 рода):

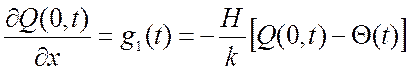,                                                  (2.56)

где     Θ(t) – температура окружающей среды;

Н – коэффициент теплообмена, т.е. количество тепла, прошедшее через единичную площадку сечения стержня за единицу времени при изменении температуры на один градус, Вт/(К·м²).

Пример 1.

Пусть стержень длиной lпогружают в пар до тех пор, пока температура во всех его точках не достигнет 100⁰С. В момент времени t=0 его боковую поверхность теплоизолируют, а его оба конца вставляют в лед при 0⁰С. Сформулировать краевую задачу для вычисления температуры стержня после выполнения сформулированных условий.

Функция Q(x,t), описывающая распределение температуры в стержне определяется уравнением:

,

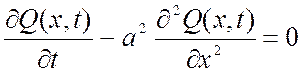где     0≤х≤l;

          а² – коэффициент температуропроводности материала стержня.

Начальные условия:

Q(x,0)=100.

Граничные условия:

Q(0,t)=Q(l,t)=0.

Пример 2.

Поставить краевую задачу определения температурного поля одномерного однослойного шара радиусом R. В начальный момент времени температурное поле подчиняется закону F(r). Шар помещен в среду с температурой Θ, при этом теплообмен на поверхности подчиняется закону Ньютона и коэффициент теплоотдачи (теплообмена) равен Н. Коэффициент теплопроводности шара k.

Так как в задаче рассматривается одномерный шар, то это означает симметричное температурное поле по всем направлениям. Тогда можете быть использовано уравнение теплопроводности в полярных координатах, которое с учетом отсутствия внутренних источников тепла имеет вид:

,

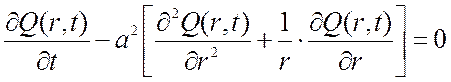Начальные условия при этом определяются заданным законом:

 .               

Граничные условия на поверхности шара запишем как граничные условия третьего рода:

.

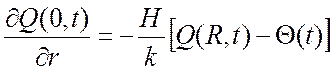Шар имеет центральную точечную симметрию. При равномерном теплообмене по поверхности температурное поле будет симметричным. В связи с этим появляются дополнительное условие симметрии:

.

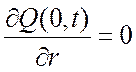Пример 3.

Для тонкого однородного стержня длиной l, начальная температура которого f(x), поставить краевую задачу об определении его температуры. При этом, температура на одном его конце х=0 поддерживается постоянной u₀, а на другом его конце х= l и на боковой поверхности происходит конвективный теплообмен по закону Ньютона с окружающей средой нулевой температуры.

Функция Q(x,t), описывающая распределение температуры в стержне определяется уравнением:

,

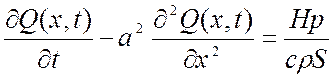где     0≤х≤l;

          а² – коэффициент температуропроводности материала стержня, м²/с;

H – коэффициент теплообмена, Вт/(К·м²);

p – периметр поперечного сечения стержня, м;

S – площадь поперечного сечения стержня, м²;

c – удельная теплоемкость вещества, Дж/(кг·К);

          ρ – плотность материала стержня, кг/м³.

Начальные условия определяются выражением:

Q(x,0)= f(x).

Граничное условие на левом конце:

Q(0,t)= u₀.

Граничное условие на правом конце:

.

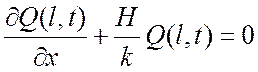2.6 Уравнение диффузии

Рассмотрим полую трубку постоянного малого сечения, в каждом сечении которой концентрацию диффундирующего вещества можно считать постоянной. Направим ось Ох вдоль трубки, тогда концентрация вещества в трубке выражается функцией Q(x,t) и может быть описана уравнением:

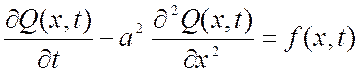,                                                         (2.57)

где     Q(x,t) – объёмная концентрация (или плотность) диффундирующего вещества, кг/м³;