Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 3

То есть должна быть задана сама функция состояния на границе области Ď.

2) Вторая краевая задача (задача Неймана, граничные условия второго рода):

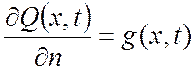, х ∂Ď, t>0.                                                       (1.13)

То есть задается градиент функции состояния на границе пространственной области.

3) Третья краевая задача (смешанная задача, граничные условия третьего рода):

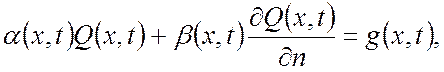 х ∂Ď, t>0,                         (1.14)

где     α(x,t), β(x,t) – заданные функции или константы на границе области.

В общем случае возможно следующее:

– на различных участках границы могут задаваться граничные условия разного типа;

– для объектов с уравнением первого порядка (одна пространственная координата), как правило, рассматривается первая краевая задача;

– граничные условия значительно упрощаются для областей Ď правильной формы (пластина, цилиндр, шар и т.д.). 

Подведем итог. Для различных классов уравнений формулируется своя краевая задача, согласно табл.1.2. В таблице использовано обозначение:

L_x – линейный оператор, содержащий саму функцию Q и ее частные производные по пространственной координате х различных порядков.

Табл.1.2

Тип уравнения	Вид уравнения	Начальные условия при t=0	Граничные условия
Гиперболический		; .	(1.9)-(1.11)
Параболический			(1.9)-(1.11)
Эллиптический		не выставляются	(1.9)-(1.11)

1.7 Основное соотношение «вход – выход»

Рассмотрим одномерную систему с распределенными параметрами, функция состояния Q(x,t) которой описывается уравнением (1.4) на пространственной области x₁≤x≤x₂. После приведения уравнения (1.4) к канонической форме записи, не содержащей смешанных производных, оно имеет вид:

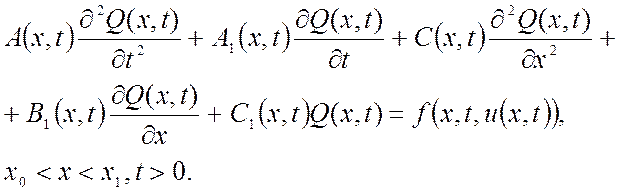                    (1.15)

Коэффициенты  уравнения (1.15) в общем случае не совпадают с коэффициентами уравнения (1.4).

Типовые начальные (1.16) и граничные (1.17)-(1.18) условия в общем рассматриваемом одномерном случае имеют вид:

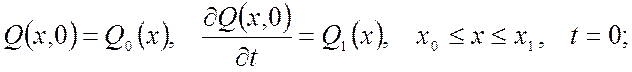                            (1.16)

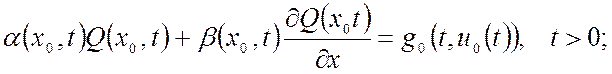                          (1.17)

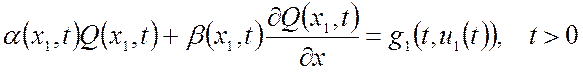.                           (1.18)

В уравнениях (1.15)-(1.18) функции f(x,t,u(x,t)), g₀(t,u₀(t)), g₁(t,u₁(t)) – входные воздействия (первое по всей пространственной области, два последних – на границе), которые в общем случае могут включать внутренние управления u(x,t), u₀(t), u₁(t), реализуемые за счет внутренних источников энергии или вещества.

Основное соотношение, связывающее выход объекта Q при заданном начальном состоянии Q₀, Q₁ с входными воздействиями f, g₀, g₁, определяется общим решением в следующей интегральной форме:

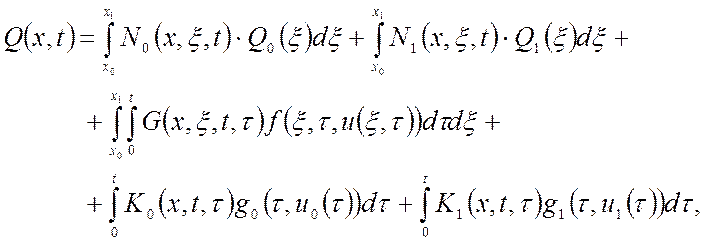         (1.19)

где     ξ, τ - переменные интегрирования по пространственной координате и

         времени соответственно (входные переменные).

Первый и второй интегралы по пространственной координате определяют составляющую общего решения, которая описывает влияние на Q(x,t) начальных распределений Q₀(x), Q₁(x).

Четвертый и пятый интегралы по времени учитывают сосредоточенные входные воздействия g₀, g₁ на границе области.

Третий интеграл – двойной интеграл по пространственно- временной области изменения пространственного ξ и временного τ аргумента распределенного входного воздействия f, отражает вклад последнего в реакцию объекта.

Функции N₀, N₁, G, K₀, K₁ - ядра линейных интегральных операторов, называемые также функциями влияния.

1.8 Функция Грина

Изменим условия в краевой задаче (1.15)-(1.18). Пусть начальные условия нулевые, а граничные условия однородные, т.е.:

, ,  t=0;                                                   (1.20)

; t>0.                                                          (1.21)

Также представим функцию f в уравнении (1.15) в виде: 

,                                                     (1.22)

где      – дельта-функции, зависящие от х и t и сосредоточенные в точках:

 и 0.

Тогда основное соотношение «вход-выход» (1.19) с учетом свойств дельта-функции сводится к виду:

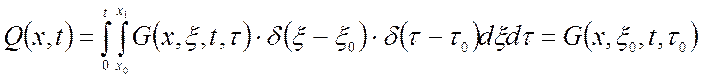.        (1.23)

То есть функция Грина – решение краевой задачи при описанных выше условиях. Она описывает реакцию распределенной системы с нулевыми начальными и однородными граничными условиями в любой точке  и любой момент времени  на точечное импульсное воздействие вида дельта-функции, приложенное в произвольной, но фиксированной точке  в момент времени .

По своему определению функция Грина удовлетворяет следующей системе уравнений:

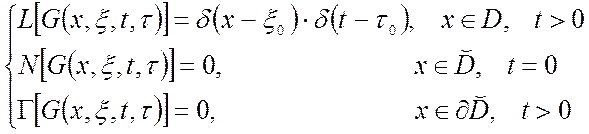                        (1.24)

Функция Грина также называется импульсной переходной функцией, функцией источника.

Широкий класс задач управления можно отнести к стационарным или автономным задачам, когда все уравнения (1.15)-(1.18) инвариантны ко времени. Другими словами, при сдвиге во времени входного воздействия без изменения его формы реакция претерпевает такой же сдвиг во времени без изменения своей формы. В этом случае функция Грина является только функцией трех аргументов и ее можно представить в виде:

,

где     t-τ – единственный аргумент, характеризующий ее зависимость.

          В частном случае, рассматривая импульсное воздействие в момент времени τ=0 функций Грина имеет вид G(x,ξ,t).

          Функция Грина во многих частных случаях может быть найдена путем непосредственного решения системы уравнений (1.24), в противном случае используются численные методы. Функции Грина для различных видов уравнений представлены в справочниках [6,14].

          Также в литературе представлены выражения, связывающие ядра N₀, N₁, K₀, K₁ уравнения (1.19) с функцией Грина, которые зависят от вида коэффициентов дифференциального оператора L и граничных условий [14].

1.9 Стандартизирующая и передаточная функции

В теории СРП можно подобрать такую функцию ω(x,t) вместо f(x,t) в уравнение (1.1), которая линейно зависит от f(x,t), Q₀(x), g(x,t) и компенсирует влияние на выходную величину ненулевых начальных и неоднородных граничных условий. При этом обеспечивается равенство решений для выходной функции Q(x,t) исходной системы (1.1) – (1.3) и краевой задачи вида: