Моделирование систем на микроуровне: Методические указания к выполнению курсовой работы, страница 8

Табл.2.1

№	Материал	G, ГПа	№	Материал	G, ГПа
1	Алмаз	478	4	Алюминий	25,5
2	Сталь	79,3	5	Полиэтилен	0,117
3	Стекло	41,4	6	Резина	0,0006

Пример.

Пусть один конец круглого однородного вала закреплен (х=0), а к другому его концу (х=l) жестко прикреплен диск с моментом инерции J. В начальный момент времени диск закручивается на угол α и отпускается без начальной скорости. Поставить краевую задачу для определения углов поворота поперечных сечений вала при t>0.

Уравнение, описывающее данный процесс имеет вид:

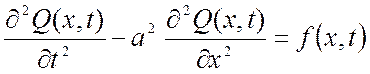,  0≤х≤l,

где     Q(x,t) – угол поворота сечения вала с координатой х в момент времени t;

f(x,t)=0;

,

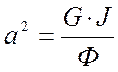где     G – модуль сдвига, Па;

Ф – осевой момент инерции единицы длины вала, кг·м.

Начальные условия при этом имеют вид:

- профиль начальных смещений

;

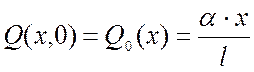- профиль начальной скорости:

.

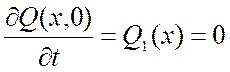Граничные условия задаются в виде:

 - жесткое закрепление левого конца;

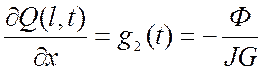 - закрепление диска с моментом инерции J.

2.4 Уравнение колебаний мембраны

Рассмотрим мембрану (тонкую пленку, в которой возникает сопротивление деформациям изгиба и сдвига), расположенную в равновесном положении в плоскости хОу. Колебания точек мембраны в направлении, перпендикулярном плоскости хОу описываются функцией Q(x,у,t) согласно уравнению:

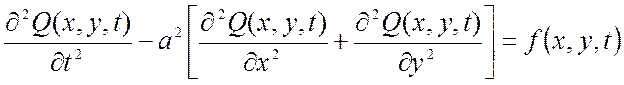,                   (2.29)

где     а – волновая скорость мембраны, м/с;

          f(x,у,t) – внешнее воздействие, м/с².

          Далее может быть использовано обозначение оператора Лапласа, которое в декартовой системе координат имеет вид (см. Приложение):

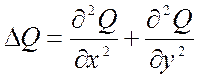.                                                                                (2.30)

С учетом оператора Лапласа (2.30) уравнение (2.29) может быть представлено в виде:

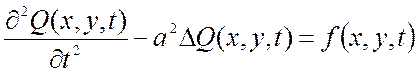.                                                           (2.31)

Волновая скорость определяется согласно выражению:

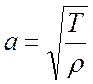,                                                                                               (2.32)

где     Т – натяжение, приложенное к контуру единичной длины, Н/м;

          ρ – поверхностная плотность (масса, приходящаяся на единицу длины площади мембраны), кг/м².

          Внешнее воздействие f(x,у,t) может быть выражено через поверхностную плотность силы g(x,у,t), т.е. силу, действующую на единицу площади (Н/м²):

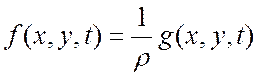.                                                                       (2.33)

Аналогично колебанию струны, в случае отсутствия внешней силы f(x,у,t)=0, получаем уравнение свободных колебаний мембраны.

Начальные условия задаются в виде:

– профиля начальных смещений мембраны:

;                                                             (2.34)

– профиля начальной скорости мембраны:

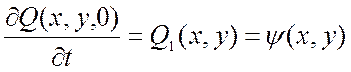.                                                          (2.35)

Граничные условия формулируются аналогично струне.

1) Так для мембраны, закрепленной на границе:

 при t≥0,

где     L – граница мембраны.

          Для квадратной мембраны (0≤х≤l₁) и (0≤у≤l₂) граничные условия запишутся в виде:

;

;                                                                            (2.36)

;

.

2) Если края мембраны свободны, т.е. они могут свободно перемещаться по вертикальной боковой поверхности цилиндра с основанием L (в случае круглой мембраны), то граничные условия имеют вид:

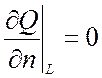.                                                                                              (2.37)

Для квадратной мембраны в этом случае условия принимают вид:

;

;   

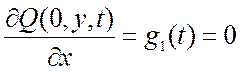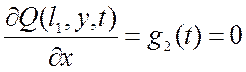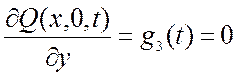;                                                                          (2.38)

.

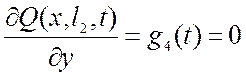3) Если края мембраны упруго закреплены, то:

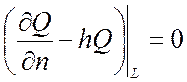,                                                                                  (2.39)

где     h=k/T;

          k – жесткость закрепления мембраны.

Описанная задача сформулирована для квадратной мембраны.

Рассмотрим случай круглой мембраны радиусом R с центром в начале координат. В этом случае удобно использовать полярные координаты r и φ. Тогда отклонение точек мембраны будет описываться функцией Q(r,φ,t), а уравнение иметь вид:

.

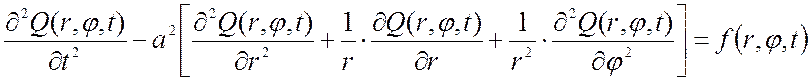Данное уравнение получено из (2.29) путем использования выражения для оператора Лапласа ΔQ в полярных координатах:

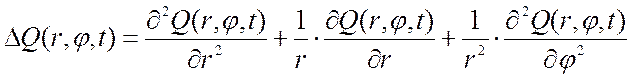.                  (2.40)

Для данной задачи начальные условия запишутся в виде:

;                                                                              (2.41)

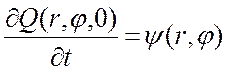.                                                                            (2.42)

Граничное условие, например, в случае жесткого закрепления мембраны:

.                                                                                       (2.43)

Если рассматривается задача об осесимметричных колебаниях мембраны, не зависящих от угла φ, уравнение упрощается и приобретает вид:

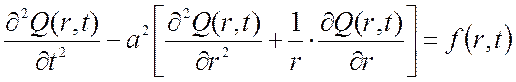.                                   (2.44)

Начальные и граничные условия при этом:

 ;                                                                                     (2.45)

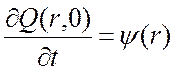;                                                                                   (2.46)

.                                                                                           (2.47)

Пример 1.

Сформулировать краевую задачу о свободных колебаниях прямоугольной мембраны (0≤х≤l₁, 0≤y≤l₂), если в начальный момент времени t=0 отклонение точек мембраны от плоскости xOy описывается функцией xy(l₁-x)(l₂-y), а начальная скорость равна нулю. Вдоль контура мембрана закреплена неподвижно.

Функция Q(x,t), описывающая свободные колебания мембраны определяется уравнением:

.

Начальные условия описываются следующим образом:

;    

.      

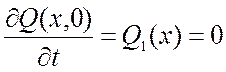Граничные условия задаются в виде:

;       ;

;        .

Пример 2.

Круглая однородная мембрана радиуса R, закрепленная по контуру, находится в состоянии равновесия при натяжении Т₀. В момент времени t=0 к поверхности мембраны приложена равномерно распределенная гармоническая сила плотностью g(r,t)=Asin(ωt). Сформулировать краевую задачу при данных условиях.