Алгоритм кратной синхронизации для регулирования расфазировки роторов виброустановки с учетом динамики привода, страница 14

 

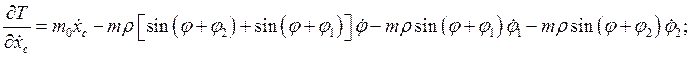
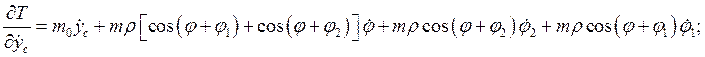
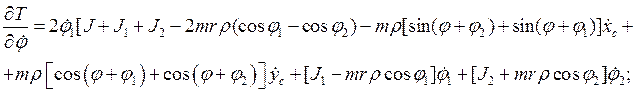
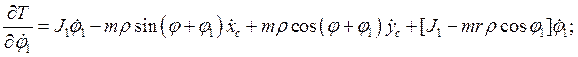
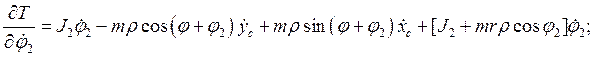
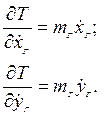
Производные по времени от полученных частных производных имеют вид:

;

;

;

; 

.

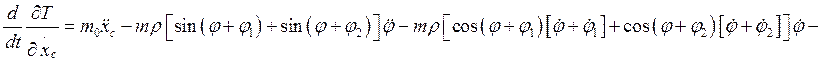
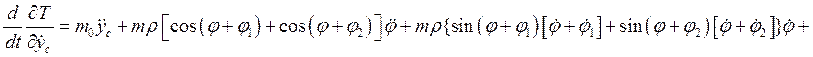
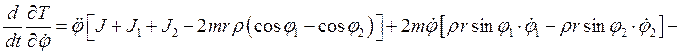
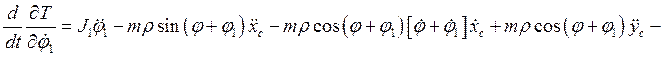
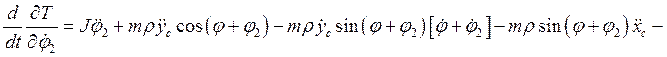
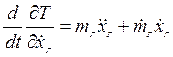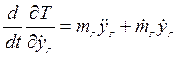Частные производные для кинетической энергии по обобщенным координатам имеют вид:

= 0;

= 0;

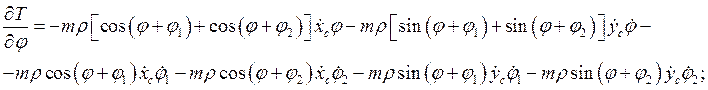
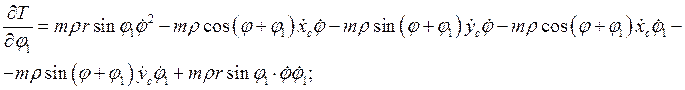
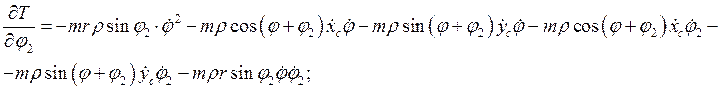
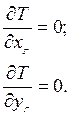
Потенциальная энергия имеет следующий вид:

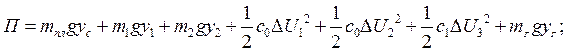         (2.20)

где с₀ – жесткость двух  нижних пружин, с₁-жесткость верхней пружины,

величина, на которую изменилась длина i-ой пружины.

Будем считать при i=1,2;

где изменение длины пружины по соответствующей оси. Поскольку, как правило, жесткости по вертикали и горизонтали различны, вместо слагаемого 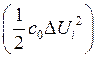 запишем 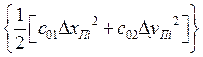, где с₀₁ - жесткость по оси X, с₀₂ - жесткость по оси Y.

Очевидно, что приращение (сжатие) пружин по соответствующим координатам составляют:

;

;

;

.

Аналогично для груза заменим:

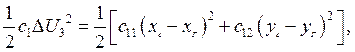, где с₁₁ и с₁₂ – жесткости верхней пружины по горизонтали и вертикали.

Тогда выражение для потенциальной энергии примет вид:

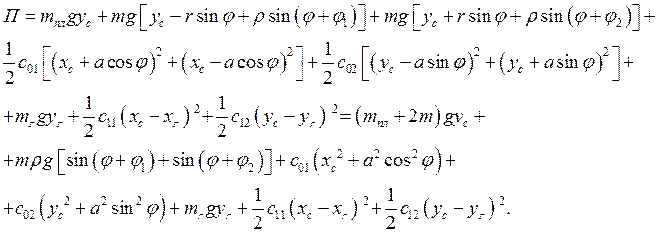(2.21)

Частные производные для потенциальной энергии по обобщенным координатам:

;

;

.

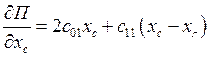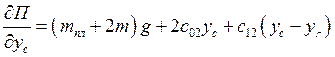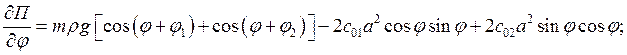
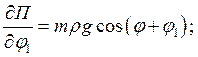
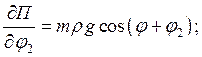
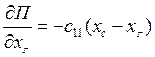
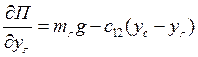Окончательно уравнения динамики примут вид:

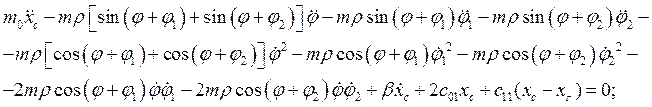
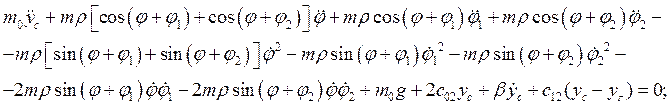
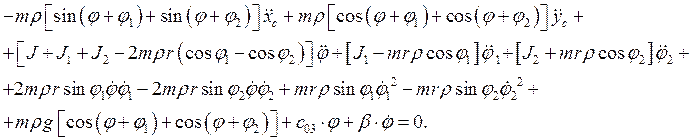
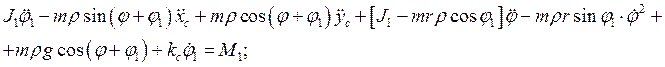
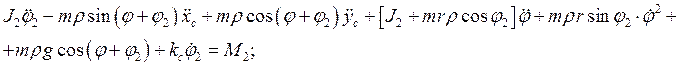
                                                        (2.22)

где - демпфирование в пружинах;

М₁, М₂ – управляющие моменты;

Считаем:

, т.кугол -мал ;

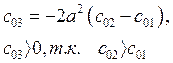
Представим уравнения в матричной форме (2.14) (рис. 2.4), выделив матрицу при вторых производных:

, где q – вектор обобщенных координат:

Рис. 2.2. Уравнения динамики в матричной форме

ГЛАВА 3

ПРИНЦИПЫ ПОСТРОЕНИЯ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ ЭЛЕКТРОМЕХАНИЧЕСКИМИ ОБЪЕКТАМИ.

Адаптивными системами управления называются модели таких систем, которые в процессе функционирования, при изменении параметров объектов или характеристик внешних воздействий, самостоятельно (без участия человека) изменяют параметры регулятора, его структуру, настройку, или регулирующее воздействие для поддержания оптимального режима работы объекта, используя при этом заранее заложенные человеком алгоритмы адаптации.

3.1. Алгоритм скоростного градиента в задачах адаптивного

управления.

Алгоритмами скоростного градиента будем называть непрерывные алгоритмы адаптации, в которых направление настраиваемых параметров или сигнала управления противоположило градиенту от изменения заданной оценочной функции в силу уравнения объекта.

Пусть дано уравнение обобщенного настраиваемого объекта (ОНО)

                                                        (3.1)

где:   х=(х₁,...,х_n) - вектор состояния ОНО

c=(c₁,...,c_n) - вектор настраиваемых параметров

ξ= (ξ ₁,..., ξ _n) - вектор неизвестных параметров объекта и внешних воздействий.

Пусть задан некоторый оценочный функционал Q_t и целью адаптации является уменьшение значения Q_t.

Оценочный функционал Q_t является неотрицательной функцией от фазовых координат ОНО : Q_t = Q(x(t),t) и такой функционал Q_t называется локальным .

В этом случае можно вычислить функцию  - скорость изменения функционала Q_t в силу уравнения (2.1) при фиксированном с. Очевидно, что , т.е. , где:     - некоторая функция, которую будем предполагать непрерывно дифференцируемой по компонентам вектора с.

Алгоритм скоростного градиента назовем следующий алгоритм адаптации:

                                                         (3.2)

где: Г=Г^Т>0 — положительно определенная N*N - матрица коэффициентов усиления.

Чтобы получить точные утверждения о свойствах системы ( 3.1 - 3.2), необходимо наложить некоторые вспомогательные условия типа гладкости и регулярности на правые части системы и функционал Q_t. Будем предполагать, что правые части ( 3.1- 3.2 ) локально ограничены равномерно по t≥0 , т.е. для любого р>0.

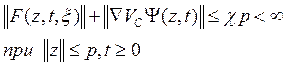                                              (3.3)

где z=(х,с) - вектор состояния системы (3.1 - 3.2 ).

Функцию Q(x,t) в случае локального функционала Q_t будем считать равномерно непрерывной по x,t, в любой области вида (x,t:||x||≤p,t≥0), Кроме того, будем требовать достаточной гладкости функций Q(x,t), F(х,с,t,x), так чтобы все их производные, возникающие в формулировках утверждений, существовали и были непрерывны по х,с.

Предположим, что цель адаптации, для достижения которой предназначен алгоритм (3.2), задается соотношением