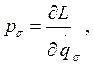Алгоритм кратной синхронизации для регулирования расфазировки роторов виброустановки с учетом динамики привода, страница 13

                                      s=1,…,k,   L=T-П                             (2.11)

называются обобщенными импульсами.

Можно установить, что обобщенные импульсы (2.11) являются линейными функциями обобщенных скоростей

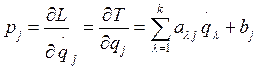
так как кинетическая энергия является определенно положительной квадратичной формой, то определитель

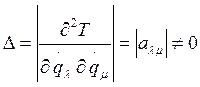
Поэтому совокупность выражений для обобщенных импульсов может быть разрешена относительно обобщенных скоростей, которые, в свою очередь, являются линейными функциями обобщенных импульсов. Подставив эти выражения для q_j в соотношение

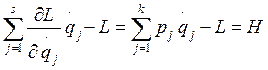                                                           (2.12)

получим функцию от переменных Гамильтона

H=H(t,q_j,p_j).

Последняя функция является определяющей для преобразованных (уравнений и называется функцией  Гамильтона. Составляя полные дифференциалы функций Н и L и проведя преобразования [10], можно получить следующие равенства:

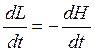
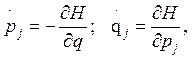                                                                                                                                                                                                                                                         j=1,…,k.                          (2.13)

Уравнения (2.13)называются уравнениями Гамильтона иликаноническими.

Если кинетическая энергия - однородная квадратичная функция обобщенных скоростей, потенциальная энергия зависит от обобщенных координат, а 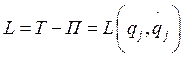, то функция Гамильтона будет равна полной механической энергии системы: Н=Т+П=Е.

Уравнения (2.13)выведены для консервативной системы.

Если помимо консервативных действуют другие силы, зависящие от обобщенных координат P_j=P_j(q_j), то уравнения Гамильтона принимают вид:

         

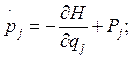
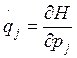
Наиболее удобная форма записи уравнений движения системы тел в обобщенных координатах может быть записана в виде:

                                          ,                                  (2.14)

где А(q) – симметричная положительно определенная матрица кинетической энергии:

,

F – обобщенные силы, в том числе применительно к вибростендам, это силы тяготения, силы диссипации в пружинах носителя, силы трения на осях роторов, управляющие моменты на осях роторов и т. п.

2.2 Динамическая модель плоского движения  вибрационного стенда СВ-2 с учетом нестационарности груза.

Расчетная схема двухроторного вибрационного стенда с присоединенным грузом, совершающего движение в вертикальной плоскости Оxy,  изображена на рис 2.1.

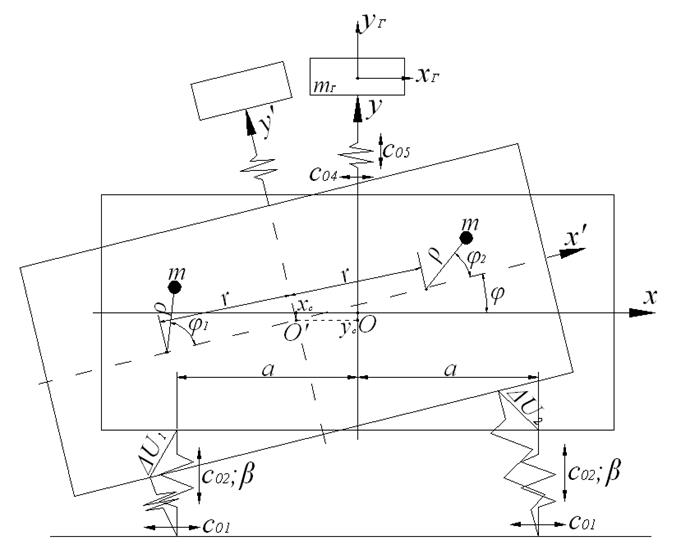
Рис. 2.1. Расчетная схема двухроторного вибрационного стенда

Система координат, связанная с платформой, обозначена 0^'х^'y^'. Координаты центра платформы – точки 0^' – обозначены {х_с, y_с}. Дебалансные роторы расположены симметрично на оси абсцисс на расстоянии r от центра 0. Платформа укреплена на упругих опорах – пружинах. Абсциссы крепления пружины Х_пi=а. Угол поворота платформы обозначен φ. Масса груза предполагается переменной  m_Г(t), координаты центра масс груза в неподвижной системе координат {х_Г , y_Г}.

Координаты дебалансых роторов, в неподвижной системе координат, моделируемых как одинаковые маятники с массой m и эксцентриситетом ρ в неподвижной системе координат, выражаются формулами:

                                        

                                 (2.15)

                                        

                                         где  ,  - углы отклонения маятников  от  горизонтали.

Кинетическая энергия четырехмассовой системы:

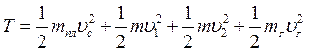                                        (2.16)

где υ_c - скорость центра масс платформы, υ_i - скорость i-го дебаланса, υ_Г - скорость груза i=1,2.

Очевидно:

;    ;    где i=1,2

Вычислим соответствующие скорости

                                                                

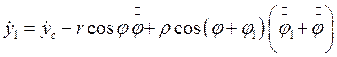                                                        (2.17)

                                                                                  

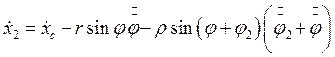
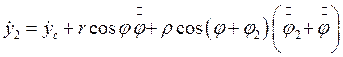
Тогда кинетическая энергия принимает вид:

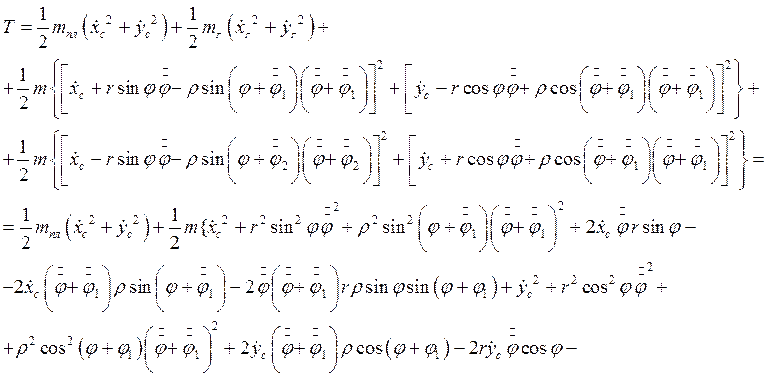
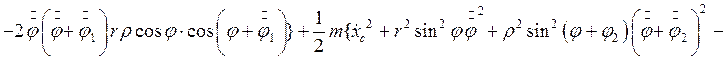
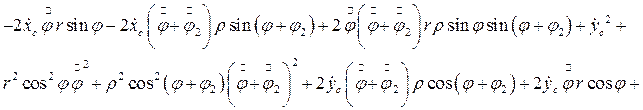
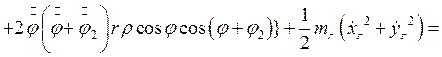                                      (2.18)

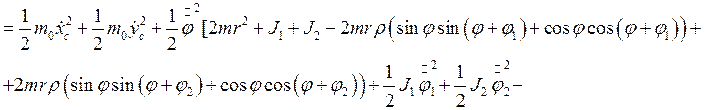
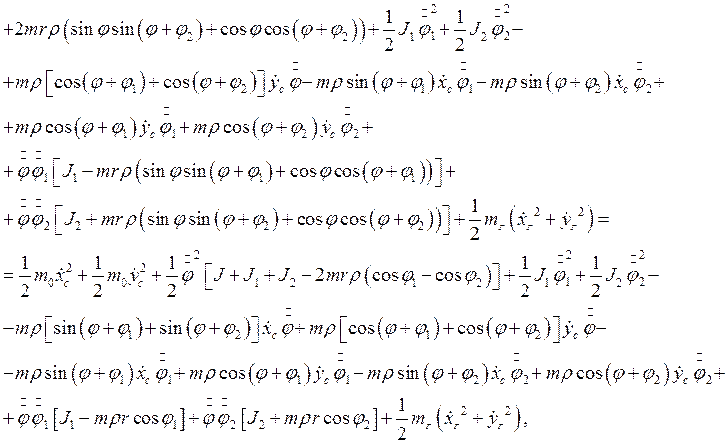
где , - момент инерции платформы.

Произведем дифференцирование в соответствии со схемой уравнений Лагранжа II рода: