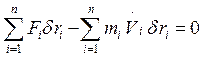Алгоритм кратной синхронизации для регулирования расфазировки роторов виброустановки с учетом динамики привода, страница 12

                                                                      (2.3)

где F_i - равнодействующая задаваемых сил, приложенных к точке системы. Первая сумма выражается через обобщенные координаты

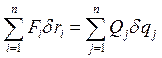                                                                          (2.4)

где Q_j- обобщенная сила.

Что касается второй суммы в уравнении (2.4), то определяя  и произведя некоторые преобразования [8], можно записать следующие соотношение

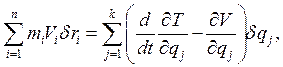
где 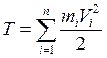 - кинетическая энергия системы.

Уравнение (2.3) теперь перепишется так:

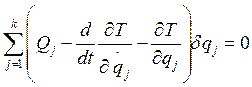
Последнее равенство может выполняться при произвольных dq_j, что возможно, если все круглые скобки равны 0. Таким образом, уравнения Лагранжа второго рода, составленные в независимых обобщенных координатах для системы с голономными связями, примут вид:

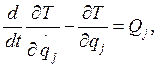                                      (j=1,2,…,k)                               (2.5)

Рассмотрим некоторые выражения обобщенных сил.

Если существует такая функция декартовых координат, называемая потенциальной энергией механической системы, а проекция некоторой силы на оси декартовой системы координат равны частным производным этой функции, взятым с обратным знаком

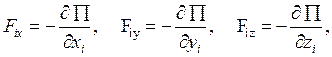                                      (2.6)

то такая сила называется консервативной.

Выражая работу сил на малых перемещениях точек системы, можно получить выражения для обобщенной силы

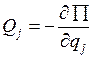                                                                                        (2.7)

при этом потенциальная энергия рассматривается как функция обобщенных координат и времени.

Если на систему действуют только консервативные силы, то уравнение Лагранжа принято записывать в форме:

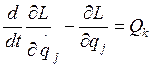                                                (j=1,2,…,k),                              (2.8)

где Q_k - непотенциальные обобщенные силы, величина  называется функцией Лагранжа.

Уравнения, описывающие взаимосвязанные электромагнитные и механические процессы в электромеханических системах и называемые уравнениями Лагранжа-Максвелла, имеют вид [8,1]:

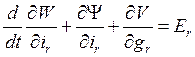                                                   (r=1,…,m);

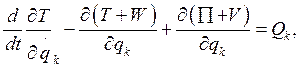                        (k=1,…,m)            (2.9)

 - кинетическая энергия; П(q₁,…,q_n) - потенциальная энергия;  - непотенциальные обобщенные силы;

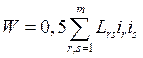 - энергия магнитного поля, причем L_rs=L_sr ; при r=s коэффициенты L_ss называют коэффициентами самоиндукции, а при r¹s - коэффициентами взаимной индукции контуров;

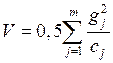 - энергия электрического поля, c_j - емкости конденсаторов.

Предполагается, что связи в системе стационарные и голономные.

Система (2.9) содержит m+n уравнений 2-го порядка относительно m+n неизвестных функций g₁(t),…,g_m(t), q₁(t),…q_n(t) Все уравнения (2.9) имеют структуру уравнений механики, то есть, если принять формально g₁(t),…,g_m(t), q₁(t),…q_n(t) за обобщенные координаты системы с кинетическим потенциалом La=T+W-(П+V), то (2.9) можно записать как уравнения Лагранжа 2-го рода этой системы. При этом первым m координатам соответствуют обобщение силы  а остальным - силы Q_k. Токи I_r имеют смысл обобщенных скоростей, W формально можно отнести к кинетической, а V - к потенциальным энергиям. Величины

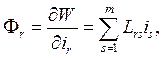                                     (r=1,…,m)                      (2.10)

называемые магнитнымипотоками или потоками индукции(вэлектротехнике - потокосцеплениями), аналогичны обобщенным импульсам; F_r есть поток вектора индукции В через любую поверхность, натянутую на r-й контур.

2.1.2. Уравнения Гамильтона для описания электромеханических систем

Как видно из вышеизложенного, состояние системы в каждый момент времени определяется 2k величинами: k обобщенными координатами q_i и k обобщеннымискоростями  может быть описано системой kобыкновенныхдифференциальныхуравнений 2-го порядка, полученныхв форме уравненийЛагранжа.

Из теории дифференциальных уравнений известно, что с помощью различных преобразований систему k дифференциальных уравнений 2-го порядка можно привести к эквивалентной ей системе 1-го порядка [9].

Преобразование, предложенное В.Р. Гамильтоном состоит в переходе к переменным t, q_s ,p_s (переменным Гамильтона), среди которых