Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 9

10.  Зная общее и частное решение записываем решение

.

в котором будет что-то конкретизировано, но не будут известны постоянные интегрирования А₁, А₂, q₁, q₂ и т.д.

11.  Используя начальные условия, определяем неизвестные постоянные интегрирования.

12.  Записываем окончательно решение дифференциального уравнения.

13.  Зная решение, можно получить значения любых других реакций цепи.

Переходные процессы в цепях 1-го порядка

I. Включение RL и RC элементов цепи на источник постоянного напряжения u(t) = U = const (табл. 1).

Таблица 1

Цепь RL	Цепь RС
1. Выбираем независимые переменные
iL(t)	uC(t)
2. Определяем начальные условия
3. Используя законы Кирхгофа, запишем интегро-дифференциальное уравнение при t = 0+ (ключ замкнут)
4. Сводим к одному дифференциальному уравнению относительно одной переменной
5. Ищем решение в виде
6. Находим характеристическое уравнение
7. Определяем корни
– постоянная времени цепи , [c]	– постоянная времени цепи , [c]
8. Зная корни, записываем общее решение
9. Находим частное решение А
10. Зная общее и частное решение, определяем общее решение как сумму общего и частного
11. Используя начальные условия, определяем постоянные интегрирования
12. Зная коэффициент А, записываем окончательное решение
13. Графики зависимости решений
14. Зная iL(t) или uC(t) можно определить другие реакции

II. Включение RL и RC элементов цепи на источник переменного напряжения  (табл. 2).

Таблица 2

Замечание 1: Анализ выражения переходного процесса для тока и напряжения показывает:

а) если  (для схемы RL) или  (для схемы RC), то в цепи сразу будет установившийся режим работы, т.е. принужденный;

б) если  (для схемы RL) или  (для схемы RC) и постоянная времени цепи много больше периода колебаний воздействия (), то в цепи возможны сверхтоки

 (для схемы RL)  и   для схемы RC).

Замечание 2: Постоянная  цепи характеризует длительность переходного процесса. Обычно считают, что переходный процесс заканчивается за время  (установившееся) = .

Замечание 3: Если известна кривая переходного процесса, то  можно определить как отрезок времени по оси времени от  до точки пересечения оси времени с касательной, проведенной к началу кривой переходного процесса (рис. 95).

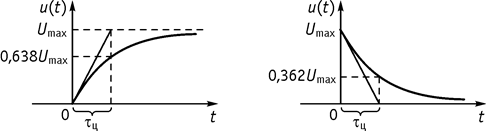
Рис. 95

Замечание 4: Переходный процесс при подключении и к источнику можно определить по формуле

.

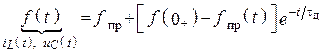III. Переходный процесс при переключении RC и RL цепи с источника постоянного напряжения  на другой .

Анализ переходного процесса приведен в таблице 3.

Таблица 3