Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 2

– эквивалентное сопротивление при согласованном включении.

– эквивалентная индуктивность при согласованном включении.

– комплексное сопротивление при согласованном включении.

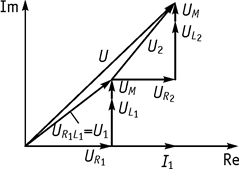
Рис. 57

.

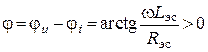Векторная диаграмма при согласованном включении приведена на рисунке 57.

 всегда .

б) Встречное включение (ток входит в разноименные зажимы) (рис. 58)

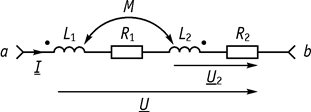
Рис. 58

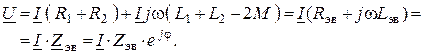
– эквивалентное сопротивление цепи.

– эквивалентная индуктивность при встречном включении.

– полное комплексное эквивалентное сопротивление.

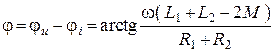
– фазовый угол.

Замечание: если , то в цепи на участке   может возникать «емкостной эффект», т.е. ток на этом участке будет опережать по фазе напряжение.

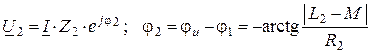
– появляется емкостный эффект

Однако цепь всегда носит индуктивный характер, так как

Замечание: Уравнения

;

могут быть положены в основу определения взаимной индукции М экспериментальным путем

1. Измерить действующие значения тока и напряжения при согласном и при встречном включении.

2. При этих измерениях определяется полное сопротивление цепи

.

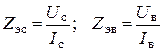3. Измерить активную мощность цепи  и вычислить активное сопротивление .

4. Определить реактивное сопротивление при встречном и согласном включении

.

.

Векторные диаграммы при встречном включении приведены на рисунке 59.

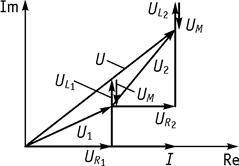
Рис. 59

Параллельное соединение индуктивно связанных элементов а) Согласное включение (рис. 60).

           

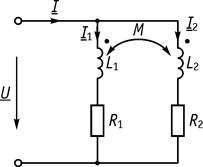
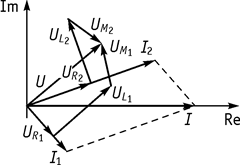
Рис. 60                                                          Рис. 61

1. Составляем ЗТК и ЗНК

;

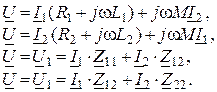
2. Определяем токи ,

,

,

(=).                                                     

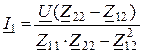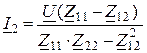3. Определяем комплексные сопротивления ветвей

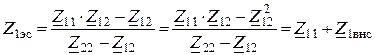 (вносимое согласное),

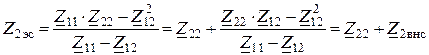, где  и  – есть сопротивления, вносимые за счет индуктивных связей.

4. Эквивалентное сопротивление ветвей цепи

.

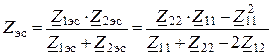5. Общий ток

.

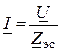Векторные диаграммы для согласованного включения приведены на рисунке 61. Построение начинаем с общего тока .

б) встречное включение (рис. 62).

          

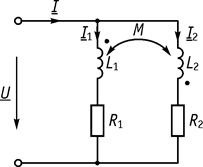
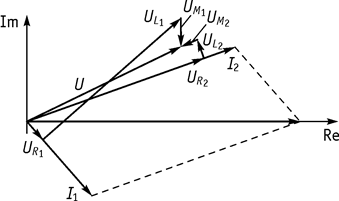
Рис. 62                                                                   Рис. 63

1. ЗНК и ЗТК

;

2. Токи в ветвях

.

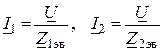3. Комплексные сопротивления ветвей

,

.

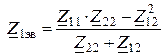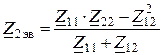4. Вносимые сопротивления

,

.

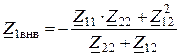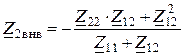5. Комплексное сопротивление всей цепи

.

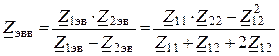6. Ток при встречном включении

.

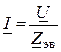Векторная диаграмма при встречном включении приведена на рисунке 63.

Особенности анализа электрических цепей с индуктивными связями

При расчете таких цепей применяется:

– Метод законов Кирхгофа.

– Метод контурных токов.

Непосредственное использование других методов (узловых напряжений, генератора, эквивалентное преобразование схем) невозможно использовать, однако если произвести развязку индуктивных связей, можно использовать все методы анализа.

Метод законов Кирхгофа

Рассмотрим схему, приведенную на рисунке 64.

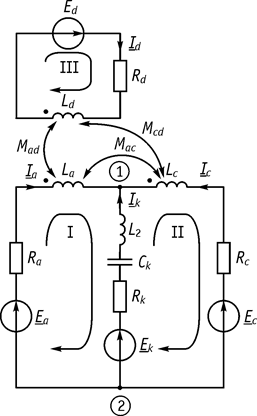
Рис. 64

1. Расставляем токи в ветвях.

2. Обозначим узлы.

3. Выбираем независимые контуры и задаем обход

4. Составляем уравнения по ЗТК и ЗНК

Замечание: при наличии взаимной индукции между k-м и l-м элементами цепи знак напряжения взаимной индукции на элементе k выбирается «+», если направление обхода k-го элемента и направление тока в этом элементе одинаковы относительно одноименных зажимов, в противном случае «–».

Для контура I

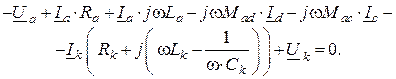
Для контура II

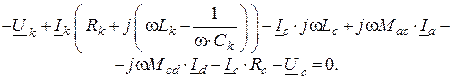
Для контура III

.

Решая совместно, определяем токи.

Развязка индуктивных связей

1. Катушки индуктивности соединены в узле одноименными зажимами. При развязки взаимная индуктивность М вносится со знаком «–» в ветви, содержащие индуктивности и «+» в 3 ветвь (рис. 65, а).

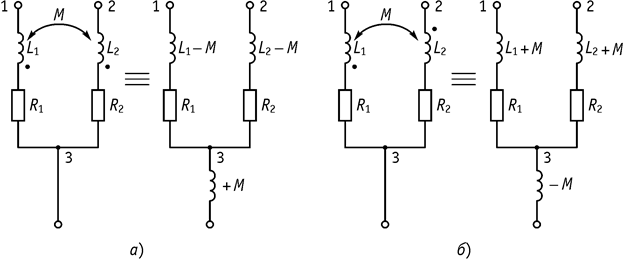
Рис. 65

2. Катушки индуктивности соединены разноименными зажимами. После развязки взаимная индуктивность вноситься со знаком «+» в ветви, содержащие индуктивность  и с «–» в 3 ветвь (рис. 65, б).

Трансформаторы

Трансформатор – устройство, предназначенное для преобразования токов, напряжений и сопротивлений.

Простейший трансформатор содержит две индуктивно связанные катушки с индуктивностями , расположенные на одном сердечнике, выполненном либо из ферромагнитного материала, либо не из ферромагнитного материала, в другом случае трансформатор называется воздушным.