Полоса пропускания и его резонансная кривая определяют избирательность контура. На входе системы действуют полезные и вредные сигналы. Колебательная система настроена на частоту f0 и имеет полосу пропускания равную диапазону полезных сигналов.
Избирательность – способность пропускать полезные сигналы и не пропускать вредные (помехи).
Колебательная система с идеальной резонансной прямой, которая идеально пропускает все полезные сигналы и не пропускает все вредные.
Так как ![]() , то при увеличении
добротности контура полоса пропускания уменьшается, а крутизна резонансной
кривой увеличивается.
, то при увеличении
добротности контура полоса пропускания уменьшается, а крутизна резонансной
кривой увеличивается.
Избирательность контура тем больше, чем больше его добротность и меньше полоса пропускания.
Коэффициенты передачи последовательного контура
Обычно последовательный контур используется для передачи напряжения сигнала (рис. 76).
Рассмотрим КПФ для L, т.е.
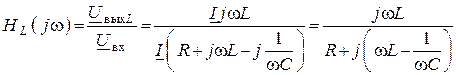 .
.
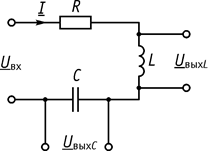
Рис. 76
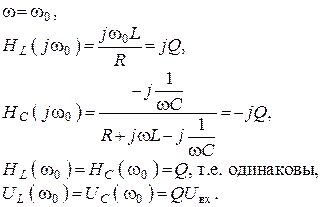
На резонансной частоте напряжение на емкости и на индуктивности в Q раз больше входного, поэтому резонанс в последовательном контуре это резонанс напряжений.
Влияние источника сигнала и нагрузки на последовательный контур
Пусть имеется схема, приведенная на рисунке 77.
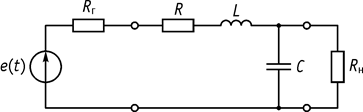
Рис. 77
1. Влияние источника. Учитывается через его внутреннее сопротивление
![]() .
.
Учет Rг дает эквивалентная добротность
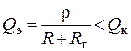 .
.
Источник сигнала уменьшает добротность контура. Это плохо, поэтому источник сигнала должен иметь Rг гораздо меньшим, а этим свойством обладает только источник напряжения, поэтому последовательный контур работает только с источниками напряжения (нельзя брать источники тока, у них большое Rг).
2. Влияние нагрузки.
Заменим параллельное соединение Rн и С эквивалентным
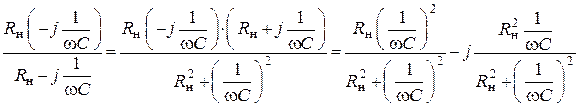 .
.
Рассмотрим область малых расстроек, т.е. w » w0
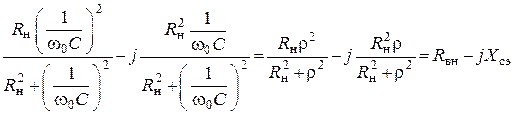 , где
, где ![]() –
вносимое сопротивление из нагрузки в контур.
–
вносимое сопротивление из нагрузки в контур.
Если
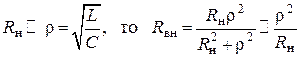 .
.
Если Rн сравнимо с r, то имеем полную формулу для вносимого сопротивления Rвн.
Активное сопротивление нагрузки может изменять
резонансную частоту контура. Если ![]() , то w0 не изменяется. Вносимое сопротивление уменьшает добротность контура
, то w0 не изменяется. Вносимое сопротивление уменьшает добротность контура
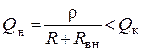 , увеличивает полосу
пропускания, уменьшает напряжение на L и С (рис.
78).
, увеличивает полосу
пропускания, уменьшает напряжение на L и С (рис.
78).
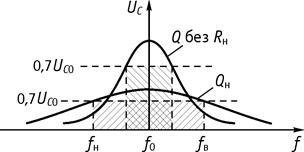
![]() Параллельный
колебательный контур
Параллельный
колебательный контур
Электрическая схема имеет вид, приведенный на рисунке 79.
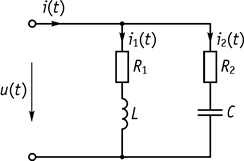
Рис. 79
Будем рассматривать
1. Контур с потерями (когда R1 и R2 нельзя пренебречь при любых частотах).
2. Контур с малыми потерями (R1 и R2 можно пренебречь при частотах близких к резонансу и частоте резонанса).
3. Контур без потерь (R1 = 0, R2 = 0).
Параллельный колебательный контур с потерями
Цель анализа (всех контуров): определить параметры и частотные характеристики параллельного колебательного контура.
1. Комплексная проводимость, полная проводимость на любой и резонансной частоте
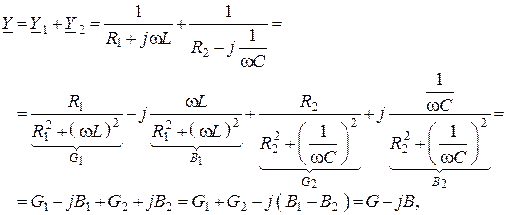
где G – активная проводимость; В – реактивная проводимость.
![]()
– полная проводимость.
![]() .
.
На резонансной частоте
![]() .
.
![]() , где
, где ![]() –
эквивалентная проводимость колебательного контура (полная проводимость на
резонансной частоте)
–
эквивалентная проводимость колебательного контура (полная проводимость на
резонансной частоте)
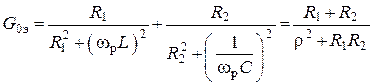 .
.
2. Резонансная частота определяется из условия резонанса токов. Фазовый сдвиг между приложенным напряжением и входным током равен 0. Откуда следует, что B = 0 или
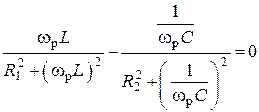 .
.
Решая это уравнение определяем wр
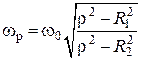 , где
, где
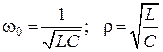 .
.
Резонанс токов возникает, если а) ![]() .
.
б) ![]() .
.
в) ![]() – случай
«безразличного» резонанса.
– случай
«безразличного» резонанса.
3. Комплексные действующие значения токов в ветвях на любой частоте
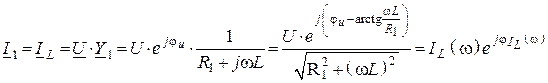 ,
,
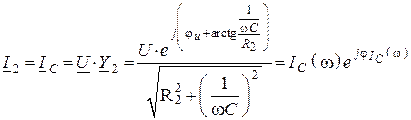 , где
, где ![]() –
действующие значения токов в ветвях.
–
действующие значения токов в ветвях.
4. Комплексное действующее значение входящего тока на любой частоте и на резонансной частоте
![]() .
.
На резонансной частоте
![]() .
.
Действующее значение
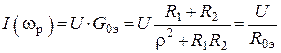 , где
, где
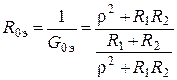
– эквивалентное резонансное сопротивление параллельного контура.
Параллельный колебательный контур с малыми потерями
Условие малых потерь
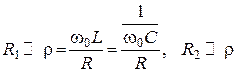 , как на резонансной частоте,
так и частотах близких к резонансной (при малых расстройках x).
, как на резонансной частоте,
так и частотах близких к резонансной (при малых расстройках x).
1. Резонансная частота
![]() .
.
2. Комплексная проводимость на любых резонансных частотах
![]() – на любой частоте,
– на любой частоте,
![]() – на резонансной частоте.
– на резонансной частоте.
Учитывая условие малых потерь можно сомножителем R1R2 пренебречь,
т.к. R1R2 ![]()
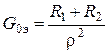 .
.
3. Эквивалентное комплексное сопротивление на любой частоте, на частоте резонанса и в режиме малых расстроек на любой частоте
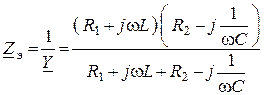 .
.
На резонансной частоте
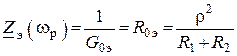 .
.
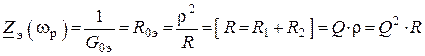 .
.
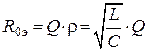 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.