Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 18

Анализ переходного процесса частотным методом

На вход цепи (рис. 132, а) подается воздействие в виде прямоугольного импульса (рис. 132, б).

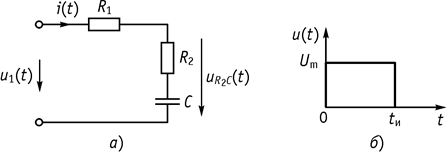
Рис. 132

Анализ:

1. Находим спектральную комплексную плотность

.

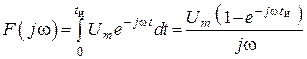2. Найдем комплексную передаточную функцию

.

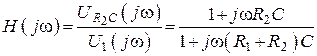3. Зная первое и второе, найдем спектр выходного сигнала

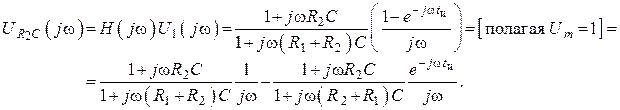
4. Заменим  на р и перейдем к функции от р

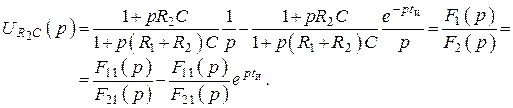
5. Найдем полюсы функции

;  ;  .

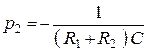Один корень равен нулю, следовательно, необходимо воспользоваться

                        ;   .

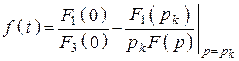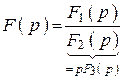6. Зная полюсы, воспользуемся теоремой запаздывания и формулами разложения, найдем оригинал функции

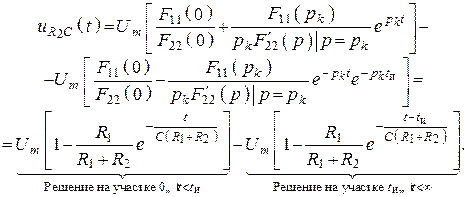
График, полагая , , изображен на рисунке 133.

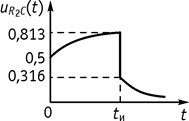
Рис. 133

Распределение энергии в непериодическом сигнале

Пусть задан сигнал в виде .

1. Определим энергию сигнала

.

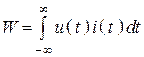2. Пусть задано сопротивление  Ом и сигнал проходит через это сопротивление, тогда

.

3. Подставим вместо тока   в первый пункт

.

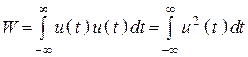4. Представим сигнал через спектр, где  – спектр сигнала.

.

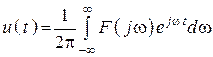5. Подставим в третий пункт вместо  выражение через спектр

.

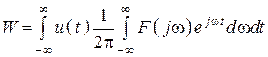Поскольку операция интегрирования линейная, тогда в интеграле можно переставить подынтегральное выражение. Получим

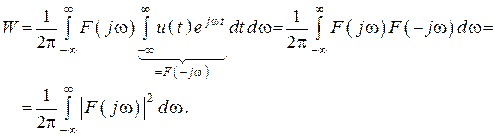
Равенство Парсеваля или теорема Рэлея

.

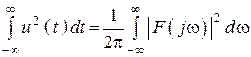Физический смысл

Энергия, рассеиваемая на сопротивлении 10 Ом равна площади под квадратом АЧХ цепи.

Условия безыскаженной передачи сигнала через линейную электрическую цепь

Частотный метод анализа цепи позволяет определить линейное искажение при прохождении сигнала через линейную электрическую цепь. Определим требования к АЧХ и ФЧХ цепи при неискаженной передаче сигнала.

Пусть имеется электрическая цепь с комплексной передаточной функцией  и на вход этой цепи подается сигнал  (рис. 134, а), имеющий спектр .

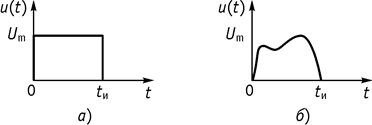
Рис. 134

При прохождении сигнала каждая составляющая спектра будет изменена в соответствии с модулем  по амплитуде, и будет изменяться по фазе . Поэтому выходной сигнал может измениться как по амплитуде, так и по форме (рис. 134, б).

Для того чтобы форма сигнала на выходе не менялась (изменение по амплитуде не является искажением), необходимо, чтобы:

во всем диапазоне частот сигнала (рис. 135, а), а  была бы линейной во всем диапазоне частот (рис. 135, б)

.

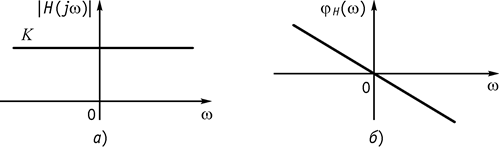
Рис. 135

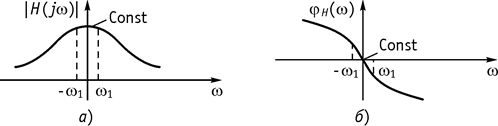
Рис. 136

Реализовать это можно лишь идеальной линейной электрической цепью. Реальные же цепи содержат реактивные элементы, следовательно, реализовать условия можно в довольно узком диапазоне частот (рис. 136).

Если входной сигнал имеет спектр больше диапазона частот безыскаженной передачи, то это приводит к линейным частотным искажениям сигнала.

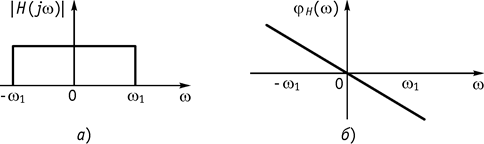
Рис. 137

Определим эти искажения (их вид) при передаче соответственно:

а) единичного скачка;

б) -функции;

в) прямоугольного импульса.

а) Через электрическую цепь в виде идеального фильтра нижних частот, имеющего следующую комплексную передаточную функцию (рис. 137)

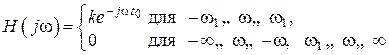
подаем единичный скачок (рис. 138).

Рис. 138

Алгоритм анализа

1. Определяем спектр входного сигнала:

.

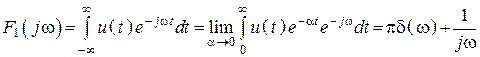2. Находим спектр выходного сигнала

.

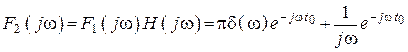3. Зная спектр выходного сигнала, найдем оригинал (сигнал)

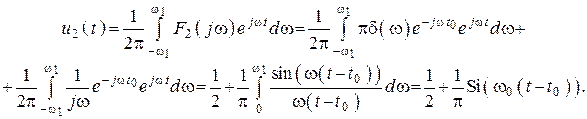
Рис. 139

4. График представлен на рисунке 139.

б) Подаем на вход d-функцию (рис. 140).

Алгоритм

1. .

2. .

3. Зная спектр выходного сигнала, определим сигнал (оригинал)

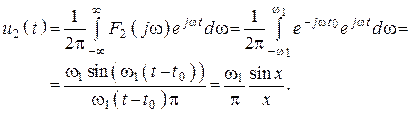
4. График представлен на рисунке 141.

Рис. 141

Из графика видно, что при подаче  на выходе получается функция  при условии ,  с задержкой на .

в) Подадим на вход прямоугольный импульс (рис. 142).

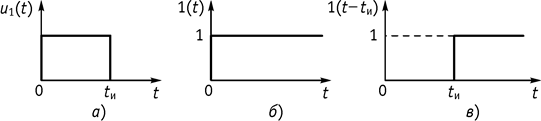
Рис. 142

необходимо определить . Алгоритм тот же.

Связь между частотными и временными характеристиками цепи

1. ;  .

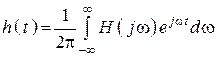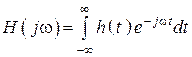2. .

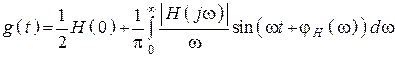3. .

.

.

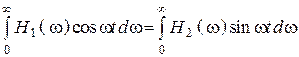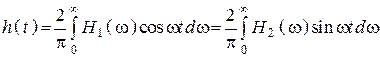4. Условия физической реализуемости цепи

 при .

5. Предельное соотношение

– при подаче на вход цепи единичного скачка на выходе цепи в момент коммутации при  появляется сигнал скачком, если АЧХ цепи имеет бесконечную полосу.

– при подаче на вход единичного скачка принужденная составляющая на выходе цепи не будет равна нулю, если передаточная функция не равна нулю на нулевой частоте.