Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 10

Цепь RL	Цепь RС
1. Определяем ток в индуктивности и напряжение на C, в момент времени t = 0–
2. Определим независимые начальные условия, используя законы коммутации
3. Для времени  и далее составляем однородные дифференциальные уравнения
4. Записываем однородное дифференциальное уравнение
5. Определяем характеристическое уравнение, для этого подставим в дифференциальное уравнение решение для свободной составляющей
6. Записываем общее решение
7. Определяем частное решение (принужденную составляющую при t = )
8. Зная общее и частотное решение, записываем решение как сумму
9. Используя начальные условия, найдем постоянные интегрирования
10. Зная постоянные интегрирования, записываем окончательное решение
11. Графики построим для

Замечание 1: Если известны  и , то можно найти

,   .

Замечание 2: При переключении  и  цепи с источника постоянного напряжения  на сопротивление нагрузки  (вместо ) алгоритм анализа остается прежним, только в этом случае принужденный режим = 0, а

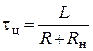 (для RL цепи), 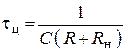  (для RC цепи).

Переходные процессы в линейных электрических цепях второго порядка

Включение последовательных соединений R, L, C элементов (последовательный контур) к источнику постоянного напряжения (рис. 96)

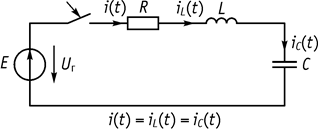
Рис. 96

Цель анализа: найти токи в цепи и напряжение на элементах цепи при

Алгоритм:

1. Определяем ток в цепи и напряжение на емкости в момент времени

,   .

2. Находим независимые начальные условия, используя законы коммутации

,  

– нулевые начальные условия.

3. Для  записываем дифференциальное уравнение цепи, используя ЗНК

.

Выбираем независимую переменную (возьмем )

;

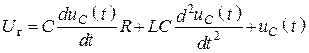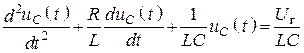
– неоднородное дифференциальное уравнение второго порядка.

4. Дифференциальное уравнение (однородное)

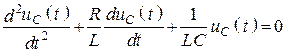
5. Найдем характеристическое уравнение, подставив в однородное дифференциальное уравнение ,

.

6. Найдем корни характеристического уравнения

.

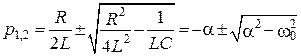Возможны следующие корни:

а) Вещественные и разные.

б) Вещественные и кратные.

в) Комплексно-сопряженные.

7. Зная корни, запишем общее решение а) ;

б) ;

в) , где .

8. Находим частное решение (принужденные составляющие  и  при )

,   .

9. Запишем решение, как сумму общего и частного для трех случаев а) ;

б) ;

в) .

Здесь  и q – неизвестные постоянные интегрирования. Для их определения необходимо составлять два уравнения. Первое уравнение этих систем получим, используя решение дифференциального уравнения и независимые начальные условия для напряжения на емкости. Второе уравнение получим, используя начальные условия для тока в индуктивности, но для этого надо сначала найти выражение тока в индуктивности.

10. Используя независимые начальные условия для напряжения на емкости, найдем первое уравнение а) , следовательно, .

 – первое уравнение.

б) , следовательно, .

 – первое уравнение.

в) , следовательно,

 – первое уравнение.

11. Определяем выражение для тока в индуктивности для а, б, в случаев, помня, что

.

а) ;

б) ;

в) .

12. Зная, выражение для тока определяем, второе уравнение, используя независимые начальные условия.

а) ,

 – второе уравнение.

б) ,

 – второе уравнение.

в) ,

 – второе уравнение.

13. Решая совместно, получаем а)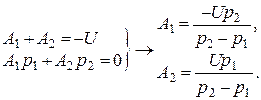

б)

в)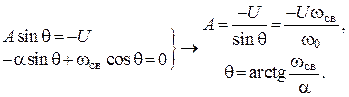

14. Зная постоянные интегрирования, записываем окончательное решение а) ;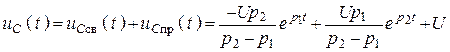

б) ;

в) .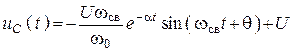

15. Зная напряжение на емкости и понимая, что ток в цепи  равен току через индуктивность , поэтому найдем значения тока, а, зная ток, определим напряжение на индуктивности.