Мгновенная, средняя, реактивная, комплексная и полная мощности в электрической цепи при гармоническом воздействии, страница 14

Квадрат модуля операторной передаточной функции (квадрат АЧХ)

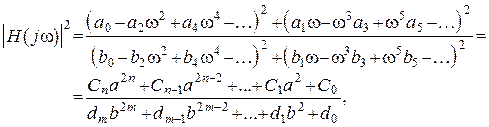, где  – представляют собой объединение коэффициентов при одинаковых степенях w.

Свойства квадрата АЧХ

1. Четная дробно-рациональная функция.

2. .

3. Значение не может принимать отрицательных или бесконечно больших значений на всей действующей оси .

Временные методы анализа переходных процессов

Временные методы анализа переходных процессов базируются на импульсной и переходной характеристиках цепи.

Импульсная характеристика цепи  – отношение реакции цепи на воздействие в виде единичной импульсной функции  (функции Дирака) к значению площади импульса при нулевых начальных условиях

.

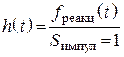Реакцией может быть напряжение или ток в любой ветви, воздействие может быть в виде источника тока и источника напряжения.

Размерность: ; .

Передаточная функция цепи  – отношение реакции цепи на воздействие единичной функции в виде  к значению этой функции, т.е. к 1 при нулевых начальных условиях

.

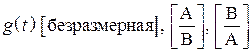В качестве реакции – напряжение на любом элементе или ток в любой ветви. В качестве воздействия – источник тока или напряжения.

Связь между  и

 – если нет скачка функции  (рис. 112, а)

или

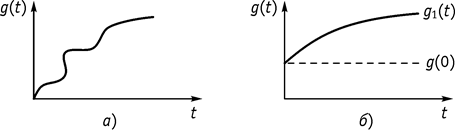
Рис. 112

 – если есть скачок  (рис. 112, б).

.

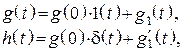
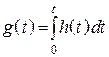Связь между  и .

Связь устанавливается прямым и обратным преобразованием Лапласа:

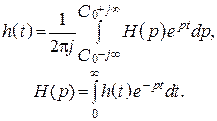
Связь между  и  установим из следующего:

поскольку 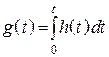, а , то учитывая свойства интегрирования по параметру, получим

.

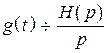Связь между  и  устанавливается с помощью прямого и обратного преобразования Фурье

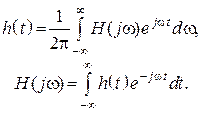
Связь между  и

.

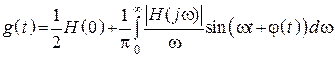Переходные и импульсные характеристики простейших RL, RC цепи

Анализ простейших RL и RC цепей приведен в таблице 5.

Таблица 5

Анализ переходных процессов методом интеграла Дюамеля. Вывод интеграла Дюамеля

Имеется цепь с переходной характеристикой , на вход этой цепи воздействует источник сигнала, приведенного на рисунке 113.

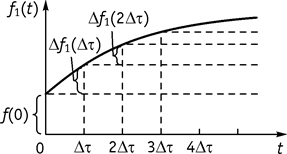
Рис. 113

Алгоритм вывода:

1. Представим входной сигнал в виде суммы сигналов сдвинутых друг от друга на Dt

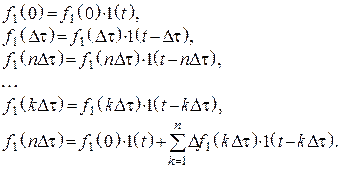
2. Зная воздействие и  найдем реакцию цепи

.

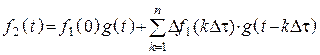3. Умножим и разделим на , и переходим к пределу при

.

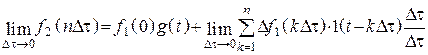Первая форма интеграла Дюамеля

.

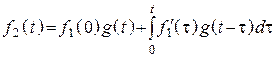Вторая форма интеграла Дюамеля

.

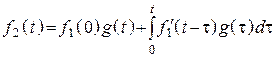Третья форма интеграла Дюамеля

.

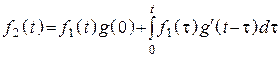Четвертая форма интеграла Дюамеля

.

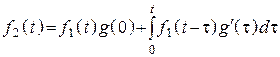Замечание: первое слагаемое правой части учитывает скачек функции. Если функция имеет скачки при , тогда формула интеграла Дюамеля приобретает вид

.

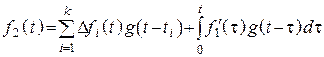 имеет знак «+», если при скачке функция увеличивается.

 имеет знак «–», если при скачке функция уменьшается.

Пример анализа простейших RL и RC цепей приведен в таблице 6.

Таблица 6

Анализ переходных процессов методом интеграла свертка

Вывод интеграла.

Пусть на вход цепи, имеющей  поступает сигнал вида, представленного на рисунке 114.

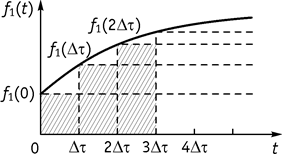
Рис. 114

1. Заменим входной сигнал суммой импульсных сигналов, имеющих ширину , амплитуду

.

2. Запишем выражение для k-го импульса